├── draw
├── __init__.py
└── draw.py
├── gqn
├── __init__.py
├── training.py
├── gqn.py
├── representation.py
└── generator.py
├── scripts
├── gpu.sh
├── data.sh
└── tfrecord-converter.py
├── placeholder.py
├── LICENSE.md
├── environment.yml
├── README.md
├── shepardmetzler.py
├── run-draw.py
├── run-convdraw.py
├── run-gqn.py
└── mental-rotation.ipynb
/draw/__init__.py:
--------------------------------------------------------------------------------
1 | from .draw import DRAW, ConvolutionalDRAW
2 |
--------------------------------------------------------------------------------
/gqn/__init__.py:
--------------------------------------------------------------------------------
1 | from .generator import GeneratorNetwork
2 | from .representation import TowerRepresentation, PyramidRepresentation
3 | from .gqn import GenerativeQueryNetwork
4 | from .training import partition, Annealer
--------------------------------------------------------------------------------
/scripts/gpu.sh:
--------------------------------------------------------------------------------
1 | #!/usr/bin/env bash
2 | export CUDA_VISIBLE_DEVICES=0,1
3 |
4 | DATA_DIR=$1
5 |
6 | # Start TensorBoard in background
7 | tensorboard --logdir "../logs" &
8 | TENSORBOARD_PID=$!
9 | echo "Started Tensorboard with PID: $TENSORBOARD_PID"
10 |
11 | # Start training script
12 | python ../run-gqn.py \
13 | --data_dir $DATA_DIR \
14 | --log_dir "../logs" \
15 | --data_parallel "True" \
16 | --batch_size 1 \
17 | --workers 6
18 |
--------------------------------------------------------------------------------
/placeholder.py:
--------------------------------------------------------------------------------
1 | import torch
2 | from torch.utils.data import Dataset
3 |
4 |
5 | class PlaceholderData(Dataset):
6 | """
7 | Random placeholder dataset for testing
8 | training loop without loading actual data.
9 | """
10 | def __init__(self, *args, **kwargs):
11 | super(PlaceholderData, self).__init__()
12 |
13 | def __len__(self):
14 | return 2000
15 |
16 | def __getitem__(self, idx):
17 | # (b, m, c, h, w)
18 | images = torch.randn(64, 15, 3, 64, 64)
19 |
20 | # (b, m, 5)
21 | viewpoints = torch.randn(64, 15, 7)
22 |
23 | return images, viewpoints
24 |
--------------------------------------------------------------------------------
/scripts/data.sh:
--------------------------------------------------------------------------------
1 | #!/usr/bin/env bash
2 |
3 | LOCATION=$1 # example: /tmp/data
4 | BATCH_SIZE=$2 # example: 64
5 |
6 | echo "Downloading data"
7 | gsutil -m cp -R gs://gqn-dataset/shepard_metzler_5_parts $LOCATION
8 |
9 | echo "Deleting small records" # less than 10MB
10 | DATA_PATH="$LOCATION/shepard_metzler_5_parts/**/*.tfrecord"
11 | find $DATA_PATH -type f -size -10M | xargs rm
12 |
13 | echo "Converting data"
14 | python tfrecord-converter.py $LOCATION shepard_metzler_5_parts -b $BATCH_SIZE -m "train"
15 | echo "Training data: done"
16 | python tfrecord-converter.py $LOCATION shepard_metzler_5_parts -b $BATCH_SIZE -m "test"
17 | echo "Testing data: done"
18 |
19 | echo "Removing original records"
20 | rm -rf "$LOCATION/shepard_metzler_5_parts/**/*.tfrecord"
--------------------------------------------------------------------------------
/LICENSE.md:
--------------------------------------------------------------------------------
1 | MIT License (MIT)
2 | =====================
3 |
4 | Copyright © 2018 Jesper Wohlert
5 |
6 | Permission is hereby granted, free of charge, to any person
7 | obtaining a copy of this software and associated documentation
8 | files (the “Software”), to deal in the Software without
9 | restriction, including without limitation the rights to use,
10 | copy, modify, merge, publish, distribute, sublicense, and/or sell
11 | copies of the Software, and to permit persons to whom the
12 | Software is furnished to do so, subject to the following
13 | conditions:
14 |
15 | The above copyright notice and this permission notice shall be
16 | included in all copies or substantial portions of the Software.
17 |
18 | THE SOFTWARE IS PROVIDED “AS IS”, WITHOUT WARRANTY OF ANY KIND,
19 | EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES
20 | OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND
21 | NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT
22 | HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY,
23 | WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING
24 | FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR
25 | OTHER DEALINGS IN THE SOFTWARE.
26 |
27 | Clauses:
28 | Permission is NOT granted to individuals who copy or clone this
29 | repository and then redistribute the code. In that case the repository
30 | should instead be forked such that the original ownership is clear.
31 |
--------------------------------------------------------------------------------
/environment.yml:
--------------------------------------------------------------------------------
1 | name: gqn
2 | channels:
3 | - pytorch
4 | - defaults
5 | dependencies:
6 | - _tflow_1100_select=0.0.1=gpu
7 | - _tflow_190_select=0.0.3=mkl
8 | - blas=1.0=mkl
9 | - cffi=1.11.5=py35he75722e_1
10 | - cudatoolkit=9.0=h13b8566_0
11 | - cudnn=7.1.2=cuda9.0_0
12 | - cupti=9.0.176=0
13 | - glib=2.56.2=hd408876_0
14 | - intel-openmp=2019.0=117
15 | - libffi=3.2.1=hd88cf55_4
16 | - libgcc-ng=8.2.0=hdf63c60_1
17 | - libgfortran-ng=7.3.0=hdf63c60_0
18 | - libprotobuf=3.6.0=hdbcaa40_0
19 | - mkl=2018.0.3=1
20 | - mkl_fft=1.0.6=py35h7dd41cf_0
21 | - mkl_random=1.0.1=py35h4414c95_1
22 | - nccl=1.3.5=cuda9.0_0
23 | - numpy=1.15.2=py35h1d66e8a_0
24 | - numpy-base=1.15.2=py35h81de0dd_0
25 | - pip=10.0.1=py35_0
26 | - protobuf=3.6.0=py35hf484d3e_0
27 | - python=3.5.6=hc3d631a_0
28 | - setuptools=40.2.0=py35_0
29 | - six=1.11.0=py35_1
30 | - tensorboard=1.10.0=py35hf484d3e_0
31 | - tensorflow=1.10.0=gpu_py35h566a776_0
32 | - tensorflow-base=1.10.0=gpu_py35h6ecc378_0
33 | - tensorflow-gpu=1.10.0=hf154084_0
34 | - ignite=0.1.1=py35_0
35 | - pytorch=1.0.0=py3.5_cuda9.0.176_cudnn7.4.1_1
36 | - pytorch-nightly=1.0.0.dev20181010=py3.5_cuda9.0.176_cudnn7.1.2_0
37 | - torchvision=0.2.1=py_2
38 | - pip:
39 | - nvidia-ml-py==375.53.1
40 | - nvidia-ml-py3==7.352.0
41 | - pytorch-ignite==0.1.1
42 | - tensorboardx==1.6
43 | - torch==1.0.0
44 | prefix: ~/.conda/envs/gqn
45 |
46 |
--------------------------------------------------------------------------------
/gqn/training.py:
--------------------------------------------------------------------------------
1 | import random
2 |
3 |
4 | class Annealer(object):
5 | def __init__(self, init, delta, steps):
6 | self.init = init
7 | self.delta = delta
8 | self.steps = steps
9 | self.s = 0
10 | self.data = self.__repr__()
11 | self.recent = init
12 |
13 | def __repr__(self):
14 | return {"init": self.init, "delta": self.delta, "steps": self.steps, "s": self.s}
15 |
16 | def __iter__(self):
17 | return self
18 |
19 | def __next__(self):
20 | self.s += 1
21 | value = max(self.delta + (self.init - self.delta) * (1 - self.s / self.steps), self.delta)
22 | self.recent = value
23 | return value
24 |
25 |
26 | def partition(images, viewpoints):
27 | """
28 | Partition batch into context and query sets.
29 | :param images
30 | :param viewpoints
31 | :return: context images, context viewpoint, query image, query viewpoint
32 | """
33 | # Maximum number of context points to use
34 | _, b, m, *x_dims = images.shape
35 | _, b, m, *v_dims = viewpoints.shape
36 |
37 | # "Squeeze" the batch dimension
38 | images = images.view((-1, m, *x_dims))
39 | viewpoints = viewpoints.view((-1, m, *v_dims))
40 |
41 | # Sample random number of views
42 | n_context = random.randint(2, m - 1)
43 | indices = random.sample([i for i in range(m)], n_context)
44 |
45 | # Partition into context and query sets
46 | context_idx, query_idx = indices[:-1], indices[-1]
47 |
48 | x, v = images[:, context_idx], viewpoints[:, context_idx]
49 | x_q, v_q = images[:, query_idx], viewpoints[:, query_idx]
50 |
51 | return x, v, x_q, v_q
--------------------------------------------------------------------------------
/README.md:
--------------------------------------------------------------------------------
1 | **Update 2019/06/24**: A model trained on 10% of the Shepard-Metzler dataset has been added, the following notebook explains the main features of this model: [nbviewer](https://nbviewer.jupyter.org/github/wohlert/generative-query-network-pytorch/blob/master/mental-rotation.ipynb)
2 |
3 | # Generative Query Network
4 |
5 | This is a PyTorch implementation of the Generative Query Network (GQN)
6 | described in the DeepMind paper "Neural scene representation and
7 | rendering" by Eslami et al. For an introduction to the model and problem
8 | described in the paper look at the article by [DeepMind](https://deepmind.com/blog/neural-scene-representation-and-rendering/).
9 |
10 | 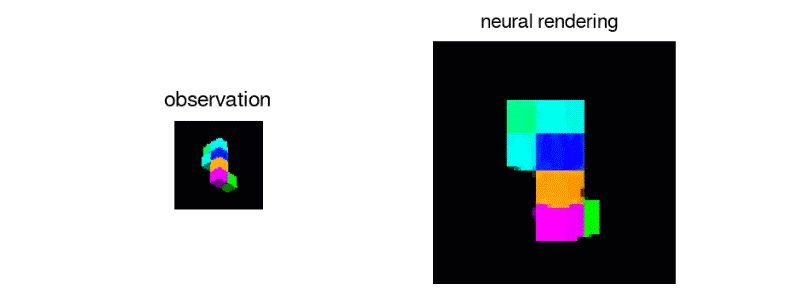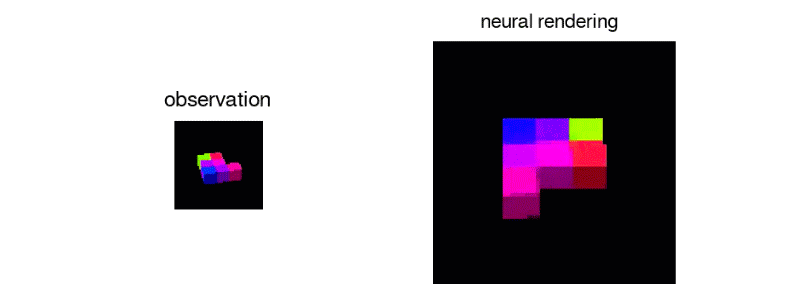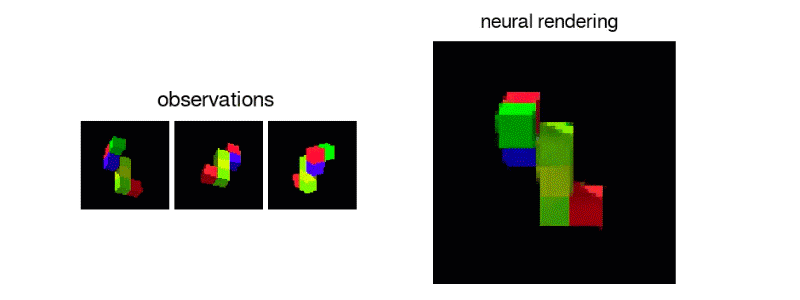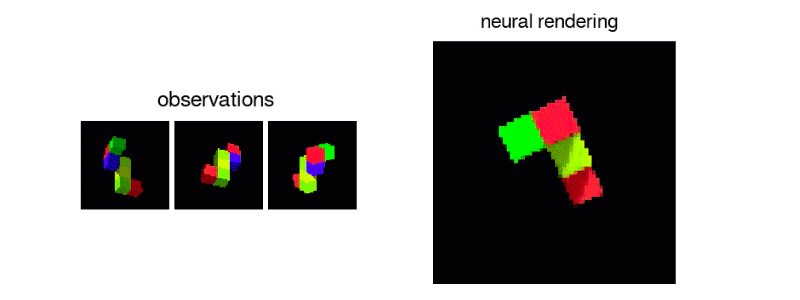
11 |
12 | The current implementation generalises to any of the datasets described
13 | in the paper. However, currently, *only the Shepard-Metzler dataset* has
14 | been implemented. To use this dataset you can use the provided script in
15 | ```
16 | sh scripts/data.sh data-dir batch-size
17 | ```
18 |
19 | The model can be trained in full by in accordance to the paper by running the
20 | file `run-gqn.py` or by using the provided training script
21 | ```
22 | sh scripts/gpu.sh data-dir
23 | ```
24 |
25 | ## Implementation
26 |
27 | The implementation shown in this repository consists of all of the
28 | representation architectures described in the paper along with the
29 | generative model that is similar to the one described in
30 | "Towards conceptual compression" by Gregor et al.
31 |
32 | Additionally, this repository also contains implementations of the **DRAW
33 | model and the ConvolutionalDRAW** model both described by Gregor et al.
34 |
35 |
--------------------------------------------------------------------------------
/shepardmetzler.py:
--------------------------------------------------------------------------------
1 | import os, gzip
2 | import numpy as np
3 | import torch
4 | from torch.utils.data import Dataset
5 |
6 |
7 | def transform_viewpoint(v):
8 | """
9 | Transforms the viewpoint vector into a consistent
10 | representation
11 | """
12 | w, z = torch.split(v, 3, dim=-1)
13 | y, p = torch.split(z, 1, dim=-1)
14 |
15 | # position, [yaw, pitch]
16 | view_vector = [w, torch.cos(y), torch.sin(y), torch.cos(p), torch.sin(p)]
17 | v_hat = torch.cat(view_vector, dim=-1)
18 |
19 | return v_hat
20 |
21 |
22 | class ShepardMetzler(Dataset):
23 | """
24 | Shepart Metzler mental rotation task
25 | dataset. Based on the dataset provided
26 | in the GQN paper. Either 5-parts or
27 | 7-parts.
28 | :param root_dir: location of data on disc
29 | :param train: whether to use train of test set
30 | :param transform: transform on images
31 | :param fraction: fraction of dataset to use
32 | :param target_transform: transform on viewpoints
33 | """
34 | def __init__(self, root_dir, train=True, transform=None, fraction=1.0, target_transform=transform_viewpoint):
35 | super(ShepardMetzler, self).__init__()
36 | assert fraction > 0.0 and fraction <= 1.0
37 | prefix = "train" if train else "test"
38 | self.root_dir = os.path.join(root_dir, prefix)
39 | self.records = sorted([p for p in os.listdir(self.root_dir) if "pt" in p])
40 | self.records = self.records[:int(len(self.records)*fraction)]
41 | self.transform = transform
42 | self.target_transform = target_transform
43 |
44 | def __len__(self):
45 | return len(self.records)
46 |
47 | def __getitem__(self, idx):
48 | scene_path = os.path.join(self.root_dir, self.records[idx])
49 | with gzip.open(scene_path, "r") as f:
50 | data = torch.load(f)
51 | images, viewpoints = list(zip(*data))
52 |
53 | images = np.stack(images)
54 | viewpoints = np.stack(viewpoints)
55 |
56 | # uint8 -> float32
57 | images = images.transpose(0, 1, 4, 2, 3)
58 | images = torch.FloatTensor(images)/255
59 |
60 | if self.transform:
61 | images = self.transform(images)
62 |
63 | viewpoints = torch.FloatTensor(viewpoints)
64 | if self.target_transform:
65 | viewpoints = self.target_transform(viewpoints)
66 |
67 | return images, viewpoints
68 |
69 |
--------------------------------------------------------------------------------
/gqn/gqn.py:
--------------------------------------------------------------------------------
1 | import torch
2 | import torch.nn as nn
3 | from torch.distributions import Normal
4 |
5 | from .representation import TowerRepresentation
6 | from .generator import GeneratorNetwork
7 |
8 |
9 | class GenerativeQueryNetwork(nn.Module):
10 | """
11 | Generative Query Network (GQN) as described
12 | in "Neural scene representation and rendering"
13 | [Eslami 2018].
14 |
15 | :param x_dim: number of channels in input
16 | :param v_dim: dimensions of viewpoint
17 | :param r_dim: dimensions of representation
18 | :param z_dim: latent channels
19 | :param h_dim: hidden channels in LSTM
20 | :param L: Number of refinements of density
21 | """
22 | def __init__(self, x_dim, v_dim, r_dim, h_dim, z_dim, L=12):
23 | super(GenerativeQueryNetwork, self).__init__()
24 | self.r_dim = r_dim
25 |
26 | self.generator = GeneratorNetwork(x_dim, v_dim, r_dim, z_dim, h_dim, L)
27 | self.representation = TowerRepresentation(x_dim, v_dim, r_dim, pool=True)
28 |
29 | def forward(self, context_x, context_v, query_x, query_v):
30 | """
31 | Forward through the GQN.
32 |
33 | :param x: batch of context images [b, m, c, h, w]
34 | :param v: batch of context viewpoints for image [b, m, k]
35 | :param x_q: batch of query images [b, c, h, w]
36 | :param v_q: batch of query viewpoints [b, k]
37 | """
38 | # Merge batch and view dimensions.
39 | b, m, *x_dims = context_x.shape
40 | _, _, *v_dims = context_v.shape
41 |
42 | x = context_x.view((-1, *x_dims))
43 | v = context_v.view((-1, *v_dims))
44 |
45 | # representation generated from input images
46 | # and corresponding viewpoints
47 | phi = self.representation(x, v)
48 |
49 | # Seperate batch and view dimensions
50 | _, *phi_dims = phi.shape
51 | phi = phi.view((b, m, *phi_dims))
52 |
53 | # sum over view representations
54 | r = torch.sum(phi, dim=1)
55 |
56 | # Use random (image, viewpoint) pair in batch as query
57 | x_mu, kl = self.generator(query_x, query_v, r)
58 |
59 | # Return reconstruction and query viewpoint
60 | # for computing error
61 | return (x_mu, r, kl)
62 |
63 | def sample(self, context_x, context_v, query_v, sigma):
64 | """
65 | Sample from the network given some context and viewpoint.
66 |
67 | :param context_x: set of context images to generate representation
68 | :param context_v: viewpoints of `context_x`
69 | :param viewpoint: viewpoint to generate image from
70 | :param sigma: pixel variance
71 | """
72 | batch_size, n_views, _, h, w = context_x.shape
73 |
74 | _, _, *x_dims = context_x.shape
75 | _, _, *v_dims = context_v.shape
76 |
77 | x = context_x.view((-1, *x_dims))
78 | v = context_v.view((-1, *v_dims))
79 |
80 | phi = self.representation(x, v)
81 |
82 | _, *phi_dims = phi.shape
83 | phi = phi.view((batch_size, n_views, *phi_dims))
84 |
85 | r = torch.sum(phi, dim=1)
86 |
87 | x_mu = self.generator.sample((h, w), query_v, r)
88 | return x_mu
89 |
--------------------------------------------------------------------------------
/run-draw.py:
--------------------------------------------------------------------------------
1 | from tqdm import tqdm
2 | import argparse
3 |
4 | import torch
5 | import torch.nn as nn
6 | import torch.nn.functional as F
7 | from torch.utils.data import DataLoader
8 | import torchvision.transforms as transforms
9 | from torchvision.datasets import MNIST
10 | from torchvision.utils import save_image
11 |
12 | from draw import DRAW
13 | cuda = torch.cuda.is_available()
14 | device = torch.device("cuda:0" if cuda else "cpu")
15 |
16 |
17 | if __name__ == '__main__':
18 | parser = argparse.ArgumentParser(description='DRAW with MNIST Example')
19 | parser.add_argument('--epochs', type=int, default=100, help='number of epochs to train (default: 100)')
20 | parser.add_argument('--batch_size', type=int, default=64, help='size of batch (default: 64)')
21 | parser.add_argument('--data_dir', type=str, help='location of training data', default="./train")
22 | parser.add_argument('--workers', type=int, help='number of data loading workers', default=2)
23 | parser.add_argument('--data_parallel', type=bool, help='whether to parallelise based on data (default: False)', default=False)
24 |
25 | args = parser.parse_args()
26 |
27 | # Define dataset
28 | transform = transforms.Compose([
29 | transforms.ToTensor(),
30 | transforms.Lambda(lambda x: torch.bernoulli(x))
31 | ])
32 | dataset = MNIST(root=args.data_dir, train=True, download=True, transform=transform)
33 |
34 | # Create model and optimizer
35 | model = DRAW(x_dim=784, h_dim=256, z_dim=16, T=10).to(device)
36 | model = nn.DataParallel(model) if args.data_parallel else model
37 | optimizer = torch.optim.Adam(model.parameters(), lr=1e-3, betas=(0.5, 0.999))
38 | scheduler = torch.optim.lr_scheduler.StepLR(optimizer, 10, 0.5)
39 |
40 | # Load the dataset
41 | kwargs = {'num_workers': args.workers, 'pin_memory': True} if cuda else {}
42 | loader = DataLoader(dataset, batch_size=args.batch_size, shuffle=True, **kwargs)
43 |
44 | loss = nn.BCELoss(reduce=False).to(device)
45 |
46 | for epoch in range(args.epochs):
47 | for x, _ in tqdm(loader):
48 | batch_size = x.size(0)
49 |
50 | x = x.view(batch_size, -1).to(device)
51 |
52 | x_hat, kl_divergence = model(x)
53 | x_hat = torch.sigmoid(x_hat)
54 |
55 | reconstruction = loss(x_hat, x).sum(1)
56 | kl = kl_divergence.sum(1)
57 | elbo = torch.mean(reconstruction + kl)
58 |
59 | elbo.backward()
60 | optimizer.step()
61 | optimizer.zero_grad()
62 |
63 | with torch.no_grad():
64 | scheduler.step()
65 |
66 | if epoch % 1 == 0:
67 | print("Loss at step {}: {}".format(epoch, elbo.item()))
68 |
69 | # Not sustainable if not dataparallel
70 | if type(model) is nn.DataParallel:
71 | x_sample = model.module.sample(args.batch_size)
72 | else:
73 | x_sample = model.sample(args.batch_size)
74 |
75 | save_image(x_hat, "reconstruction-{}.jpg".format(epoch))
76 | save_image(x_sample, "sample-{}.jpg".format(epoch))
77 |
78 | if epoch % 10 == 0:
79 | torch.save(model, "model-{}.pt".format(epoch))
80 |
--------------------------------------------------------------------------------
/scripts/tfrecord-converter.py:
--------------------------------------------------------------------------------
1 | """
2 | tfrecord-converter
3 |
4 | Takes a directory of tf-records with Shepard-Metzler data
5 | and converts it into a number of gzipped PyTorch records
6 | with a fixed batch size.
7 |
8 | Thanks to l3robot and versatran01 for providing initial
9 | scripts.
10 | """
11 | import os, gzip, torch
12 | import tensorflow as tf, numpy as np, multiprocessing as mp
13 | from functools import partial
14 | from itertools import islice, chain
15 | from argparse import ArgumentParser
16 |
17 | # disable logging and gpu
18 | tf.logging.set_verbosity(tf.logging.ERROR)
19 | os.environ["CUDA_VISIBLE_DEVICES"] = "-1"
20 |
21 | POSE_DIM, IMG_DIM, SEQ_DIM = 5, 64, 15
22 |
23 | def chunk(iterable, size=10):
24 | """
25 | Chunks an iterator into subsets of
26 | a given size.
27 | """
28 | iterator = iter(iterable)
29 | for first in iterator:
30 | yield chain([first], islice(iterator, size - 1))
31 |
32 | def process(record):
33 | """
34 | Processes a tf-record into a numpy (image, pose) tuple.
35 | """
36 | kwargs = dict(dtype=tf.uint8, back_prop=False)
37 | for data in tf.python_io.tf_record_iterator(record):
38 | instance = tf.parse_single_example(data, {
39 | 'frames': tf.FixedLenFeature(shape=SEQ_DIM, dtype=tf.string),
40 | 'cameras': tf.FixedLenFeature(shape=SEQ_DIM * POSE_DIM, dtype=tf.float32)
41 | })
42 |
43 | # Get data
44 | images = tf.concat(instance['frames'], axis=0)
45 | poses = instance['cameras']
46 |
47 | # Convert
48 | images = tf.map_fn(tf.image.decode_jpeg, tf.reshape(images, [-1]), **kwargs)
49 | images = tf.reshape(images, (-1, SEQ_DIM, IMG_DIM, IMG_DIM, 3))
50 | poses = tf.reshape(poses, (-1, SEQ_DIM, POSE_DIM))
51 |
52 | # Numpy conversion
53 | images, poses = images.numpy(), poses.numpy()
54 | yield np.squeeze(images), np.squeeze(poses)
55 |
56 | def convert(record, batch_size):
57 | """
58 | Processes and saves a tf-record.
59 | """
60 | path, filename = os.path.split(record)
61 | basename, *_ = os.path.splitext(filename)
62 | print(basename)
63 |
64 | batch_process = lambda r: chunk(process(r), batch_size)
65 |
66 | for i, batch in enumerate(batch_process(record)):
67 | p = os.path.join(path, "{0:}-{1:02}.pt.gz".format(basename, i))
68 | with gzip.open(p, 'wb') as f:
69 | torch.save(list(batch), f)
70 |
71 | if __name__ == '__main__':
72 | tf.enable_eager_execution()
73 | parser = ArgumentParser(description='Convert gqn tfrecords to gzip files.')
74 | parser.add_argument('base_dir', nargs=1,
75 | help='base directory of gqn dataset')
76 | parser.add_argument('dataset', type=str, default="shepard_metzler_5_parts",
77 | help='datasets to convert, eg. shepard_metzler_5_parts')
78 | parser.add_argument('-b', '--batch-size', type=int, default=64,
79 | help='number of sequences in each output file')
80 | parser.add_argument('-m', '--mode', type=str, default='train',
81 | help='whether to convert train or test')
82 | args = parser.parse_args()
83 |
84 | # Find path
85 | base_dir = os.path.expanduser(args.base_dir[0])
86 | data_dir = os.path.join(base_dir, args.dataset, args.mode)
87 |
88 | # Find all records
89 | records = [os.path.join(data_dir, f) for f in sorted(os.listdir(data_dir))]
90 | records = [f for f in records if "tfrecord" in f]
91 |
92 | with mp.Pool(processes=mp.cpu_count()) as pool:
93 | f = partial(convert, batch_size=args.batch_size)
94 | pool.map(f, records)
95 |
--------------------------------------------------------------------------------
/run-convdraw.py:
--------------------------------------------------------------------------------
1 | import argparse
2 | from tqdm import tqdm
3 |
4 | import torch
5 | import torch.nn as nn
6 | import torch.nn.functional as F
7 | import torchvision.transforms as transforms
8 | from torch.utils.data import DataLoader
9 | from torchvision.datasets import SVHN, MNIST
10 | from torchvision.utils import save_image
11 |
12 | from draw import ConvolutionalDRAW
13 | cuda = torch.cuda.is_available()
14 | device = torch.device("cuda:0" if cuda else "cpu")
15 |
16 |
17 | if __name__ == '__main__':
18 | parser = argparse.ArgumentParser(description='ConvolutionalDRAW with MNIST/SVHN Example')
19 | parser.add_argument('--epochs', type=int, default=100, help='number of epochs to train (default: 100)')
20 | parser.add_argument('--data_dir', type=str, help='location of training data', default="./train")
21 | parser.add_argument('--batch_size', type=int, default=128, help='size of batch (default: 128)')
22 | parser.add_argument('--dataset', type=str, default="MNIST", help='dataset to use (default: MNIST)')
23 | parser.add_argument('--workers', type=int, help='number of data loading workers', default=2)
24 | parser.add_argument('--data_parallel', type=bool, help='whether to parallelise based on data (default: False)', default=False)
25 |
26 | args = parser.parse_args()
27 |
28 | if args.dataset == "MNIST":
29 | mean, std = 0, 1
30 | transform = transforms.Compose([
31 | transforms.ToTensor(),
32 | #transforms.Normalize(mean=(0.1307,), std=(0.3081,)
33 | transforms.Lambda(lambda x: torch.bernoulli(x))
34 | ])
35 | dataset = MNIST(root=args.data_dir, train=True, download=True, transform=transform)
36 | loss = nn.BCELoss(reduce=False)
37 | output_activation = torch.sigmoid
38 | x_dim, x_shape = 1, (28, 28)
39 |
40 | elif args.dataset == "SVHN":
41 | mean, std = (0.4376, 0.4437, 0.4728), (0.198, 0.201, 0.197)
42 | transform = transforms.Compose([
43 | transforms.ToTensor(),
44 | transforms.Normalize(mean=mean, std=std)
45 | ])
46 | dataset = SVHN(root=args.data_dir, split="train", download=True, transform=transform)
47 | loss = nn.MSELoss(reduce=False)
48 | output_activation = lambda x: x
49 | x_dim, x_shape = 3, (32, 32)
50 |
51 | # Create model and optimizer
52 | model = ConvolutionalDRAW(x_dim=x_dim, x_shape=x_shape, h_dim=160, z_dim=12, T=16).to(device)
53 | model = nn.DataParallel(model) if args.data_parallel else model
54 | optimizer = torch.optim.Adam(model.parameters(), lr=1e-3, betas=(0.9, 0.999))
55 | scheduler = torch.optim.lr_scheduler.StepLR(optimizer, 10, 0.5)
56 |
57 | # Load the dataset
58 | kwargs = {'num_workers': args.workers, 'pin_memory': True} if cuda else {}
59 | loader = DataLoader(dataset, batch_size=args.batch_size, shuffle=True, **kwargs)
60 |
61 | for epoch in range(args.epochs):
62 | for x, _ in tqdm(loader):
63 | batch_size = x.size(0)
64 | x = x.to(device)
65 |
66 | x_hat, kl = model(x)
67 | x_hat = output_activation(x_hat)
68 |
69 | reconstruction = torch.sum(loss(x_hat, x).view(batch_size, -1), dim=1)
70 | kl_divergence = torch.sum(kl.view(batch_size, -1), dim=1)
71 | elbo = torch.mean(reconstruction + kl_divergence)
72 |
73 | elbo.backward()
74 | optimizer.step()
75 | optimizer.zero_grad()
76 |
77 | with torch.no_grad():
78 | scheduler.step()
79 |
80 | if epoch % 1 == 0:
81 | print("Loss at step {}: {}".format(epoch, elbo.item()))
82 |
83 | # Not sustainable if not dataparallel
84 | x_sample = model.module.sample(args.batch_size)
85 |
86 | # Renormalize to visualise
87 | x_sample = (x_sample - mean)/std
88 | x_hat = (x_hat - mean)/std
89 |
90 | save_image(x_hat, "reconstruction-{}.jpg".format(epoch))
91 | save_image(x_sample, "sample-{}.jpg".format(epoch))
92 |
93 | if epoch % 10 == 0:
94 | torch.save(model, "model-{}.pt".format(epoch))
--------------------------------------------------------------------------------
/gqn/representation.py:
--------------------------------------------------------------------------------
1 | import torch
2 | import torch.nn as nn
3 | import torch.nn.functional as F
4 |
5 |
6 | class TowerRepresentation(nn.Module):
7 | def __init__(self, n_channels, v_dim, r_dim=256, pool=True):
8 | """
9 | Network that generates a condensed representation
10 | vector from a joint input of image and viewpoint.
11 |
12 | Employs the tower/pool architecture described in the paper.
13 |
14 | :param n_channels: number of color channels in input image
15 | :param v_dim: dimensions of the viewpoint vector
16 | :param r_dim: dimensions of representation
17 | :param pool: whether to pool representation
18 | """
19 | super(TowerRepresentation, self).__init__()
20 | # Final representation size
21 | self.r_dim = k = r_dim
22 | self.pool = pool
23 |
24 | self.conv1 = nn.Conv2d(n_channels, k, kernel_size=2, stride=2)
25 | self.conv2 = nn.Conv2d(k, k, kernel_size=2, stride=2)
26 | self.conv3 = nn.Conv2d(k, k//2, kernel_size=3, stride=1, padding=1)
27 | self.conv4 = nn.Conv2d(k//2, k, kernel_size=2, stride=2)
28 |
29 | self.conv5 = nn.Conv2d(k + v_dim, k, kernel_size=3, stride=1, padding=1)
30 | self.conv6 = nn.Conv2d(k + v_dim, k//2, kernel_size=3, stride=1, padding=1)
31 | self.conv7 = nn.Conv2d(k//2, k, kernel_size=3, stride=1, padding=1)
32 | self.conv8 = nn.Conv2d(k, k, kernel_size=1, stride=1)
33 |
34 | self.avgpool = nn.AvgPool2d(k//16)
35 |
36 | def forward(self, x, v):
37 | """
38 | Send an (image, viewpoint) pair into the
39 | network to generate a representation
40 | :param x: image
41 | :param v: viewpoint (x, y, z, cos(yaw), sin(yaw), cos(pitch), sin(pitch))
42 | :return: representation
43 | """
44 | # Increase dimensions
45 | v = v.view(v.size(0), -1, 1, 1)
46 | v = v.repeat(1, 1, self.r_dim // 16, self.r_dim // 16)
47 |
48 | # First skip-connected conv block
49 | skip_in = F.relu(self.conv1(x))
50 | skip_out = F.relu(self.conv2(skip_in))
51 |
52 | x = F.relu(self.conv3(skip_in))
53 | x = F.relu(self.conv4(x)) + skip_out
54 |
55 | # Second skip-connected conv block (merged)
56 | skip_in = torch.cat([x, v], dim=1)
57 | skip_out = F.relu(self.conv5(skip_in))
58 |
59 | x = F.relu(self.conv6(skip_in))
60 | x = F.relu(self.conv7(x)) + skip_out
61 |
62 | r = F.relu(self.conv8(x))
63 |
64 | if self.pool:
65 | r = self.avgpool(r)
66 |
67 | return r
68 |
69 |
70 | class PyramidRepresentation(nn.Module):
71 | def __init__(self, n_channels, v_dim, r_dim=256):
72 | """
73 | Network that generates a condensed representation
74 | vector from a joint input of image and viewpoint.
75 |
76 | Employs the pyramid architecture described in the paper.
77 |
78 | :param n_channels: number of color channels in input image
79 | :param v_dim: dimensions of the viewpoint vector
80 | :param r_dim: dimensions of representation
81 | """
82 | super(PyramidRepresentation, self).__init__()
83 | # Final representation size
84 | self.r_dim = k = r_dim
85 |
86 | self.conv1 = nn.Conv2d(n_channels + v_dim, k//8, kernel_size=2, stride=2)
87 | self.conv2 = nn.Conv2d(k//8, k//4, kernel_size=2, stride=2)
88 | self.conv3 = nn.Conv2d(k//4, k//2, kernel_size=2, stride=2)
89 | self.conv4 = nn.Conv2d(k//2, k, kernel_size=8, stride=8)
90 |
91 | def forward(self, x, v):
92 | """
93 | Send an (image, viewpoint) pair into the
94 | network to generate a representation
95 | :param x: image
96 | :param v: viewpoint (x, y, z, cos(yaw), sin(yaw), cos(pitch), sin(pitch))
97 | :return: representation
98 | """
99 | # Increase dimensions
100 | batch_size, _, h, w = x.shape
101 |
102 | v = v.view(batch_size, -1, 1, 1)
103 | v = v.repeat(1, 1, h, w)
104 |
105 | # Merge representation
106 | r = torch.cat([x, v], dim=1)
107 |
108 | r = F.relu(self.conv1(r))
109 | r = F.relu(self.conv2(r))
110 | r = F.relu(self.conv3(r))
111 | r = F.relu(self.conv4(r))
112 |
113 | return r
--------------------------------------------------------------------------------
/run-gqn.py:
--------------------------------------------------------------------------------
1 | """
2 | run-gqn.py
3 |
4 | Script to train the a GQN on the Shepard-Metzler dataset
5 | in accordance to the hyperparameter settings described in
6 | the supplementary materials of the paper.
7 | """
8 | import random
9 | import math
10 | from argparse import ArgumentParser
11 |
12 | # Torch
13 | import torch
14 | import torch.nn as nn
15 | from torch.distributions import Normal
16 | from torch.utils.data import DataLoader
17 | from torchvision.utils import make_grid
18 |
19 | # TensorboardX
20 | from tensorboardX import SummaryWriter
21 |
22 | # Ignite
23 | from ignite.contrib.handlers import ProgressBar
24 | from ignite.engine import Engine, Events
25 | from ignite.handlers import ModelCheckpoint, Timer
26 | from ignite.metrics import RunningAverage
27 |
28 | from gqn import GenerativeQueryNetwork, partition, Annealer
29 | from shepardmetzler import ShepardMetzler
30 | #from placeholder import PlaceholderData as ShepardMetzler
31 |
32 | cuda = torch.cuda.is_available()
33 | device = torch.device("cuda:0" if cuda else "cpu")
34 |
35 | # Random seeding
36 | random.seed(99)
37 | torch.manual_seed(99)
38 | if cuda: torch.cuda.manual_seed(99)
39 | torch.backends.cudnn.deterministic = True
40 | torch.backends.cudnn.benchmark = False
41 |
42 | if __name__ == '__main__':
43 | parser = ArgumentParser(description='Generative Query Network on Shepard Metzler Example')
44 | parser.add_argument('--n_epochs', type=int, default=200, help='number of epochs run (default: 200)')
45 | parser.add_argument('--batch_size', type=int, default=1, help='multiple of batch size (default: 1)')
46 | parser.add_argument('--data_dir', type=str, help='location of data', default="train")
47 | parser.add_argument('--log_dir', type=str, help='location of logging', default="log")
48 | parser.add_argument('--fraction', type=float, help='how much of the data to use', default=1.0)
49 | parser.add_argument('--workers', type=int, help='number of data loading workers', default=4)
50 | parser.add_argument('--data_parallel', type=bool, help='whether to parallelise based on data (default: False)', default=False)
51 | args = parser.parse_args()
52 |
53 | # Create model and optimizer
54 | model = GenerativeQueryNetwork(x_dim=3, v_dim=7, r_dim=256, h_dim=128, z_dim=64, L=8).to(device)
55 | model = nn.DataParallel(model) if args.data_parallel else model
56 |
57 | optimizer = torch.optim.Adam(model.parameters(), lr=5 * 10 ** (-5))
58 |
59 | # Rate annealing schemes
60 | sigma_scheme = Annealer(2.0, 0.7, 80000)
61 | mu_scheme = Annealer(5 * 10 ** (-6), 5 * 10 ** (-6), 1.6 * 10 ** 5)
62 |
63 | # Load the dataset
64 | train_dataset = ShepardMetzler(root_dir=args.data_dir, fraction=args.fraction)
65 | valid_dataset = ShepardMetzler(root_dir=args.data_dir, fraction=args.fraction, train=False)
66 |
67 | kwargs = {'num_workers': args.workers, 'pin_memory': True} if cuda else {}
68 | train_loader = DataLoader(train_dataset, batch_size=args.batch_size, shuffle=True, **kwargs)
69 | valid_loader = DataLoader(valid_dataset, batch_size=args.batch_size, shuffle=True, **kwargs)
70 |
71 | def step(engine, batch):
72 | model.train()
73 |
74 | x, v = batch
75 | x, v = x.to(device), v.to(device)
76 | x, v, x_q, v_q = partition(x, v)
77 |
78 | # Reconstruction, representation and divergence
79 | x_mu, _, kl = model(x, v, x_q, v_q)
80 |
81 | # Log likelihood
82 | sigma = next(sigma_scheme)
83 | ll = Normal(x_mu, sigma).log_prob(x_q)
84 |
85 | likelihood = torch.mean(torch.sum(ll, dim=[1, 2, 3]))
86 | kl_divergence = torch.mean(torch.sum(kl, dim=[1, 2, 3]))
87 |
88 | # Evidence lower bound
89 | elbo = likelihood - kl_divergence
90 | loss = -elbo
91 | loss.backward()
92 |
93 | optimizer.step()
94 | optimizer.zero_grad()
95 |
96 | with torch.no_grad():
97 | # Anneal learning rate
98 | mu = next(mu_scheme)
99 | i = engine.state.iteration
100 | for group in optimizer.param_groups:
101 | group["lr"] = mu * math.sqrt(1 - 0.999 ** i) / (1 - 0.9 ** i)
102 |
103 | return {"elbo": elbo.item(), "kl": kl_divergence.item(), "sigma": sigma, "mu": mu}
104 |
105 | # Trainer and metrics
106 | trainer = Engine(step)
107 | metric_names = ["elbo", "kl", "sigma", "mu"]
108 | RunningAverage(output_transform=lambda x: x["elbo"]).attach(trainer, "elbo")
109 | RunningAverage(output_transform=lambda x: x["kl"]).attach(trainer, "kl")
110 | RunningAverage(output_transform=lambda x: x["sigma"]).attach(trainer, "sigma")
111 | RunningAverage(output_transform=lambda x: x["mu"]).attach(trainer, "mu")
112 | ProgressBar().attach(trainer, metric_names=metric_names)
113 |
114 | # Model checkpointing
115 | checkpoint_handler = ModelCheckpoint("./", "checkpoint", save_interval=1, n_saved=3,
116 | require_empty=False)
117 | trainer.add_event_handler(event_name=Events.EPOCH_COMPLETED, handler=checkpoint_handler,
118 | to_save={'model': model.state_dict, 'optimizer': optimizer.state_dict,
119 | 'annealers': (sigma_scheme.data, mu_scheme.data)})
120 |
121 | timer = Timer(average=True).attach(trainer, start=Events.EPOCH_STARTED, resume=Events.ITERATION_STARTED,
122 | pause=Events.ITERATION_COMPLETED, step=Events.ITERATION_COMPLETED)
123 |
124 | # Tensorbard writer
125 | writer = SummaryWriter(log_dir=args.log_dir)
126 |
127 | @trainer.on(Events.ITERATION_COMPLETED)
128 | def log_metrics(engine):
129 | for key, value in engine.state.metrics.items():
130 | writer.add_scalar("training/{}".format(key), value, engine.state.iteration)
131 |
132 | @trainer.on(Events.EPOCH_COMPLETED)
133 | def save_images(engine):
134 | with torch.no_grad():
135 | x, v = engine.state.batch
136 | x, v = x.to(device), v.to(device)
137 | x, v, x_q, v_q = partition(x, v)
138 |
139 | x_mu, r, _ = model(x, v, x_q, v_q)
140 |
141 | r = r.view(-1, 1, 16, 16)
142 |
143 | # Send to CPU
144 | x_mu = x_mu.detach().cpu().float()
145 | r = r.detach().cpu().float()
146 |
147 | writer.add_image("representation", make_grid(r), engine.state.epoch)
148 | writer.add_image("reconstruction", make_grid(x_mu), engine.state.epoch)
149 |
150 | @trainer.on(Events.EPOCH_COMPLETED)
151 | def validate(engine):
152 | model.eval()
153 | with torch.no_grad():
154 | x, v = next(iter(valid_loader))
155 | x, v = x.to(device), v.to(device)
156 | x, v, x_q, v_q = partition(x, v)
157 |
158 | # Reconstruction, representation and divergence
159 | x_mu, _, kl = model(x, v, x_q, v_q)
160 |
161 | # Validate at last sigma
162 | ll = Normal(x_mu, sigma_scheme.recent).log_prob(x_q)
163 |
164 | likelihood = torch.mean(torch.sum(ll, dim=[1, 2, 3]))
165 | kl_divergence = torch.mean(torch.sum(kl, dim=[1, 2, 3]))
166 |
167 | # Evidence lower bound
168 | elbo = likelihood - kl_divergence
169 |
170 | writer.add_scalar("validation/elbo", elbo.item(), engine.state.epoch)
171 | writer.add_scalar("validation/kl", kl_divergence.item(), engine.state.epoch)
172 |
173 | @trainer.on(Events.EXCEPTION_RAISED)
174 | def handle_exception(engine, e):
175 | writer.close()
176 | engine.terminate()
177 | if isinstance(e, KeyboardInterrupt) and (engine.state.iteration > 1):
178 | import warnings
179 | warnings.warn('KeyboardInterrupt caught. Exiting gracefully.')
180 | checkpoint_handler(engine, { 'model_exception': model })
181 | else: raise e
182 |
183 | trainer.run(train_loader, args.n_epochs)
184 | writer.close()
185 |
--------------------------------------------------------------------------------
/gqn/generator.py:
--------------------------------------------------------------------------------
1 | """
2 | The inference-generator architecture is conceptually
3 | similar to the encoder-decoder pair seen in variational
4 | autoencoders. The difference here is that the model
5 | must infer latents from a cascade of time-dependent inputs
6 | using convolutional and recurrent networks.
7 |
8 | Additionally, a representation vector is shared between
9 | the networks.
10 | """
11 | SCALE = 4 # Scale of image generation process
12 |
13 |
14 | import torch
15 | import torch.nn as nn
16 | import torch.nn.functional as F
17 | from torch.distributions import Normal, kl_divergence
18 |
19 |
20 | class Conv2dLSTMCell(nn.Module):
21 | """
22 | 2d convolutional long short-term memory (LSTM) cell.
23 | Functionally equivalent to nn.LSTMCell with the
24 | difference being that nn.Kinear layers are replaced
25 | by nn.Conv2D layers.
26 |
27 | :param in_channels: number of input channels
28 | :param out_channels: number of output channels
29 | :param kernel_size: size of image kernel
30 | :param stride: length of kernel stride
31 | :param padding: number of pixels to pad with
32 | """
33 | def __init__(self, in_channels, out_channels, kernel_size=3, stride=1, padding=1):
34 | super(Conv2dLSTMCell, self).__init__()
35 | self.in_channels = in_channels
36 | self.out_channels = out_channels
37 |
38 | kwargs = dict(kernel_size=kernel_size, stride=stride, padding=padding)
39 |
40 | self.forget = nn.Conv2d(in_channels, out_channels, **kwargs)
41 | self.input = nn.Conv2d(in_channels, out_channels, **kwargs)
42 | self.output = nn.Conv2d(in_channels, out_channels, **kwargs)
43 | self.state = nn.Conv2d(in_channels, out_channels, **kwargs)
44 |
45 | self.transform = nn.Conv2d(out_channels, in_channels, **kwargs)
46 |
47 | def forward(self, input, states):
48 | """
49 | Send input through the cell.
50 |
51 | :param input: input to send through
52 | :param states: (hidden, cell) pair of internal state
53 | :return new (hidden, cell) pair
54 | """
55 | (hidden, cell) = states
56 |
57 | input = input + self.transform(hidden)
58 |
59 | forget_gate = torch.sigmoid(self.forget(input))
60 | input_gate = torch.sigmoid(self.input(input))
61 | output_gate = torch.sigmoid(self.output(input))
62 | state_gate = torch.tanh(self.state(input))
63 |
64 | # Update internal cell state
65 | cell = forget_gate * cell + input_gate * state_gate
66 | hidden = output_gate * torch.tanh(cell)
67 |
68 | return hidden, cell
69 |
70 |
71 | class GeneratorNetwork(nn.Module):
72 | """
73 | Network similar to a convolutional variational
74 | autoencoder that refines the generated image
75 | over a number of iterations.
76 |
77 | :param x_dim: number of channels in input
78 | :param v_dim: dimensions of viewpoint
79 | :param r_dim: dimensions of representation
80 | :param z_dim: latent channels
81 | :param h_dim: hidden channels in LSTM
82 | :param L: number of density refinements
83 | :param share: whether to share cores across refinements
84 | """
85 | def __init__(self, x_dim, v_dim, r_dim, z_dim=64, h_dim=128, L=12, share=True):
86 | super(GeneratorNetwork, self).__init__()
87 | self.L = L
88 | self.z_dim = z_dim
89 | self.h_dim = h_dim
90 | self.share = share
91 |
92 | # Core computational units
93 | kwargs = dict(kernel_size=5, stride=1, padding=2)
94 | inference_args = dict(in_channels=v_dim + r_dim + x_dim + h_dim, out_channels=h_dim, **kwargs)
95 | generator_args = dict(in_channels=v_dim + r_dim + z_dim, out_channels=h_dim, **kwargs)
96 | if self.share:
97 | self.inference_core = Conv2dLSTMCell(**inference_args)
98 | self.generator_core = Conv2dLSTMCell(**generator_args)
99 | else:
100 | self.inference_core = nn.ModuleList([Conv2dLSTMCell(**inference_args) for _ in range(L)])
101 | self.generator_core = nn.ModuleList([Conv2dLSTMCell(**generator_args) for _ in range(L)])
102 |
103 | # Inference, prior
104 | self.posterior_density = nn.Conv2d(h_dim, 2*z_dim, **kwargs)
105 | self.prior_density = nn.Conv2d(h_dim, 2*z_dim, **kwargs)
106 |
107 | # Generative density
108 | self.observation_density = nn.Conv2d(h_dim, x_dim, kernel_size=1, stride=1, padding=0)
109 |
110 | # Up/down-sampling primitives
111 | self.upsample = nn.ConvTranspose2d(h_dim, h_dim, kernel_size=SCALE, stride=SCALE, padding=0, bias=False)
112 | self.downsample = nn.Conv2d(x_dim, x_dim, kernel_size=SCALE, stride=SCALE, padding=0, bias=False)
113 |
114 | def forward(self, x, v, r):
115 | """
116 | Attempt to reconstruct x with corresponding
117 | viewpoint v and context representation r.
118 |
119 | :param x: image to send through
120 | :param v: viewpoint of image
121 | :param r: representation for image
122 | :return reconstruction of x and kl-divergence
123 | """
124 | batch_size, _, h, w = x.shape
125 | kl = 0
126 |
127 | # Downsample x, upsample v and r
128 | x = self.downsample(x)
129 | v = v.view(batch_size, -1, 1, 1).repeat(1, 1, h // SCALE, w // SCALE)
130 | if r.size(2) != h // SCALE:
131 | r = r.repeat(1, 1, h // SCALE, w // SCALE)
132 |
133 | # Reset hidden and cell state
134 | hidden_i = x.new_zeros((batch_size, self.h_dim, h // SCALE, w // SCALE))
135 | cell_i = x.new_zeros((batch_size, self.h_dim, h // SCALE, w // SCALE))
136 |
137 | hidden_g = x.new_zeros((batch_size, self.h_dim, h // SCALE, w // SCALE))
138 | cell_g = x.new_zeros((batch_size, self.h_dim, h // SCALE, w // SCALE))
139 |
140 | # Canvas for updating
141 | u = x.new_zeros((batch_size, self.h_dim, h, w))
142 |
143 | for l in range(self.L):
144 | # Prior factor (eta π network)
145 | p_mu, p_std = torch.chunk(self.prior_density(hidden_g), 2, dim=1)
146 | prior_distribution = Normal(p_mu, F.softplus(p_std))
147 |
148 | # Inference state update
149 | inference = self.inference_core if self.share else self.inference_core[l]
150 | hidden_i, cell_i = inference(torch.cat([hidden_g, x, v, r], dim=1), [hidden_i, cell_i])
151 |
152 | # Posterior factor (eta e network)
153 | q_mu, q_std = torch.chunk(self.posterior_density(hidden_i), 2, dim=1)
154 | posterior_distribution = Normal(q_mu, F.softplus(q_std))
155 |
156 | # Posterior sample
157 | z = posterior_distribution.rsample()
158 |
159 | # Generator state update
160 | generator = self.generator_core if self.share else self.generator_core[l]
161 | hidden_g, cell_g = generator(torch.cat([z, v, r], dim=1), [hidden_g, cell_g])
162 |
163 | # Calculate u
164 | u = self.upsample(hidden_g) + u
165 |
166 | # Calculate KL-divergence
167 | kl += kl_divergence(posterior_distribution, prior_distribution)
168 |
169 | x_mu = self.observation_density(u)
170 |
171 | return torch.sigmoid(x_mu), kl
172 |
173 | def sample(self, x_shape, v, r):
174 | """
175 | Sample from the prior distribution to generate
176 | a new image given a viewpoint and representation
177 |
178 | :param x_shape: (height, width) of image
179 | :param v: viewpoint
180 | :param r: representation (context)
181 | """
182 | h, w = x_shape
183 | batch_size = v.size(0)
184 |
185 | # Increase dimensions
186 | v = v.view(batch_size, -1, 1, 1).repeat(1, 1, h // SCALE, w // SCALE)
187 | if r.size(2) != h // SCALE:
188 | r = r.repeat(1, 1, h // SCALE, w // SCALE)
189 |
190 | # Reset hidden and cell state for generator
191 | hidden_g = v.new_zeros((batch_size, self.h_dim, h // SCALE, w // SCALE))
192 | cell_g = v.new_zeros((batch_size, self.h_dim, h // SCALE, w // SCALE))
193 |
194 | u = v.new_zeros((batch_size, self.h_dim, h, w))
195 |
196 | for _ in range(self.L):
197 | p_mu, p_log_std = torch.chunk(self.prior_density(hidden_g), 2, dim=1)
198 | prior_distribution = Normal(p_mu, F.softplus(p_log_std))
199 |
200 | # Prior sample
201 | z = prior_distribution.sample()
202 |
203 | # Calculate u
204 | hidden_g, cell_g = self.generator_core(torch.cat([z, v, r], dim=1), [hidden_g, cell_g])
205 | u = self.upsample(hidden_g) + u
206 |
207 | x_mu = self.observation_density(u)
208 |
209 | return torch.sigmoid(x_mu)
210 |
--------------------------------------------------------------------------------
/draw/draw.py:
--------------------------------------------------------------------------------
1 | import torch
2 | import torch.nn as nn
3 | import torch.nn.functional as F
4 | from torch.distributions import Normal, kl_divergence
5 |
6 |
7 | class BaseAttention(nn.Module):
8 | """
9 | No attention module.
10 | """
11 | def __init__(self, h_dim, x_dim):
12 | super(BaseAttention, self).__init__()
13 | self.h_dim = h_dim
14 | self.x_dim = x_dim
15 | self.write_head = nn.Linear(h_dim, x_dim)
16 |
17 | def read(self, x, x_hat, h):
18 | return torch.cat([x, x_hat], dim=1)
19 |
20 | def write(self, x):
21 | return self.write_head(x)
22 |
23 |
24 | class FilterBankAttention(BaseAttention):
25 | def __init__(self, h_dim, x_dim):
26 | """
27 | Filter bank attention mechanism described in the paper.
28 | """
29 | super(FilterBankAttention, self).__init__(h_dim, x_dim)
30 |
31 | def read(self, x, error, h):
32 | return NotImplementedError
33 |
34 | def write(self, x):
35 | return NotImplementedError
36 |
37 |
38 | class DRAW(nn.Module):
39 | """
40 | Deep Recurrent Attentive Writer (DRAW) [Gregor 2015].
41 |
42 | :param x_dim: size of input
43 | :param h_dim: number of hidden neurons
44 | :param z_dim: number of latent neurons
45 | :param T: number of recurrent layers
46 | """
47 | def __init__(self, x_dim, h_dim=256, z_dim=10, T=10, attention_module=BaseAttention):
48 | super(DRAW, self).__init__()
49 | self.x_dim = x_dim
50 | self.z_dim = z_dim
51 | self.h_dim = h_dim
52 | self.T = T
53 |
54 | # Returns the distribution parameters
55 | self.variational = nn.Linear(h_dim, 2*z_dim)
56 | self.observation = nn.Linear(x_dim, x_dim)
57 |
58 | # Recurrent encoder/decoder models
59 | self.encoder = nn.LSTMCell(2*x_dim + h_dim, h_dim)
60 | self.decoder = nn.LSTMCell(z_dim, h_dim)
61 |
62 | # Attention module
63 | self.attention = attention_module(h_dim, x_dim)
64 |
65 | def forward(self, x):
66 | batch_size = x.size(0)
67 |
68 | # Hidden states (allocate on same device as input)
69 | h_enc = x.new_zeros((batch_size, self.h_dim))
70 | h_dec = x.new_zeros((batch_size, self.h_dim))
71 |
72 | # Cell states
73 | c_enc = x.new_zeros((batch_size, self.h_dim))
74 | c_dec = x.new_zeros((batch_size, self.h_dim))
75 |
76 | # Prior distribution
77 | p_mu = x.new_zeros((batch_size, self.z_dim))
78 | p_std = x.new_ones((batch_size, self.z_dim))
79 | self.prior = Normal(p_mu, p_std)
80 |
81 | canvas = x.new_zeros((batch_size, self.x_dim))
82 | kl = 0
83 |
84 | for _ in range(self.T):
85 | x_hat = x - torch.sigmoid(canvas)
86 | att = self.attention.read(x, x_hat, h_dec)
87 |
88 | # Infer posterior density from hidden state
89 | h_enc, c_enc = self.encoder(torch.cat([att, h_dec], dim=1), [h_enc, c_enc])
90 |
91 | # Posterior distribution
92 | q_mu, q_log_std = torch.split(self.variational(h_enc), self.z_dim, dim=1)
93 | q_std = torch.exp(q_log_std)
94 | posterior = Normal(q_mu, q_std)
95 |
96 | # Sample from posterior
97 | z = posterior.rsample()
98 |
99 | # Send representation through decoder
100 | h_dec, c_dec = self.decoder(z, [h_dec, c_dec])
101 |
102 | # Gather representation
103 | canvas += self.attention.write(h_dec)
104 |
105 | kl += kl_divergence(posterior, self.prior)
106 |
107 | # Return the reconstruction
108 | x_mu = self.observation(canvas)
109 | return [x_mu, kl]
110 |
111 | def sample(self, z=None):
112 | """
113 | Generate a sample from the data distribution.
114 |
115 | :param z: latent code, otherwise sample from prior
116 | """
117 | z = self.prior.sample() if z is None else z
118 | batch_size = z.size(0)
119 |
120 | canvas = z.new_zeros((batch_size, self.x_dim))
121 | h_dec = z.new_zeros((batch_size, self.h_dim))
122 | c_dec = z.new_zeros((batch_size, self.h_dim))
123 |
124 | for _ in range(self.T):
125 | h_dec, c_dec = self.decoder(z, [h_dec, c_dec])
126 | canvas = canvas + self.attention.write(h_dec)
127 |
128 | x_mu = self.observation(canvas)
129 | return x_mu
130 |
131 |
132 | class Conv2dLSTMCell(nn.Module):
133 | """
134 | 2d convolutional long short-term memory (LSTM) cell.
135 | Functionally equivalent to nn.LSTMCell with the
136 | difference being that nn.Kinear layers are replaced
137 | by nn.Conv2D layers.
138 |
139 | :param in_channels: number of input channels
140 | :param out_channels: number of output channels
141 | :param kernel_size: size of image kernel
142 | :param stride: length of kernel stride
143 | :param padding: number of pixels to pad with
144 | """
145 | def __init__(self, in_channels, out_channels, kernel_size=3, stride=1, padding=1):
146 | super(Conv2dLSTMCell, self).__init__()
147 | self.in_channels = in_channels
148 | self.out_channels = out_channels
149 |
150 | kwargs = dict(kernel_size=kernel_size, stride=stride, padding=padding)
151 |
152 | self.forget = nn.Conv2d(in_channels, out_channels, **kwargs)
153 | self.input = nn.Conv2d(in_channels, out_channels, **kwargs)
154 | self.output = nn.Conv2d(in_channels, out_channels, **kwargs)
155 | self.state = nn.Conv2d(in_channels, out_channels, **kwargs)
156 |
157 | self.transform = nn.Conv2d(out_channels, in_channels, **kwargs)
158 |
159 | def forward(self, input, states):
160 | """
161 | Send input through the cell.
162 |
163 | :param input: input to send through
164 | :param states: (hidden, cell) pair of internal state
165 | :return new (hidden, cell) pair
166 | """
167 | (hidden, cell) = states
168 |
169 | input = input + self.transform(hidden)
170 |
171 | forget_gate = torch.sigmoid(self.forget(input))
172 | input_gate = torch.sigmoid(self.input(input))
173 | output_gate = torch.sigmoid(self.output(input))
174 | state_gate = torch.tanh(self.state(input))
175 |
176 | # Update internal cell state
177 | cell = forget_gate * cell + input_gate * state_gate
178 | hidden = output_gate * torch.tanh(cell)
179 |
180 | return hidden, cell
181 |
182 |
183 | class ConvolutionalDRAW(nn.Module):
184 | """
185 | Convolutional DRAW model described in
186 | "Towards Conceptual Compression" [Gregor 2016].
187 | The model consists of a autoregressive density
188 | estimator using a recurrent convolutional network.
189 |
190 | :param x_dim: number of channels in input
191 | :param x_shape: tuple representing input image shape
192 | :param h_dim: number of hidden channels
193 | :param z_dim: number of channels in latent variable
194 | :param T: number of recurrent layers
195 | """
196 | def __init__(self, x_dim, x_shape=(32, 32), h_dim=256, z_dim=10, T=10):
197 | super(ConvolutionalDRAW, self).__init__()
198 | self.x_dim = x_dim
199 | self.x_shape = x_shape
200 | self.z_dim = z_dim
201 | self.h_dim = h_dim
202 | self.T = T
203 |
204 | # Outputs parameters of distributions
205 | self.variational = nn.Conv2d(h_dim, 2*z_dim, kernel_size=5, stride=1, padding=2)
206 | self.prior = nn.Conv2d(h_dim, 2*z_dim, kernel_size=5, stride=1, padding=2)
207 |
208 | # Analogous to original DRAW model
209 | self.write_head = nn.Conv2d(h_dim, x_dim*4, kernel_size=1, stride=1, padding=0)
210 | self.read_head = nn.Conv2d(x_dim, x_dim, kernel_size=3, stride=2, padding=1)
211 |
212 | # Recurrent encoder/decoder models
213 | self.encoder = Conv2dLSTMCell(2*x_dim, h_dim, kernel_size=5, stride=2, padding=2)
214 | self.decoder = Conv2dLSTMCell(z_dim + x_dim, h_dim, kernel_size=5, stride=1, padding=2)
215 |
216 | def forward(self, x):
217 | h, w = self.x_shape
218 | batch_size = x.size(0)
219 |
220 | # Hidden states (allocate on same device as input)
221 | h_enc = x.new_zeros((batch_size, self.h_dim, h//2, w//2))
222 | h_dec = x.new_zeros((batch_size, self.h_dim, h//2, w//2))
223 |
224 | # Cell states
225 | c_enc = x.new_zeros((batch_size, self.h_dim, h//2, w//2))
226 | c_dec = x.new_zeros((batch_size, self.h_dim, h//2, w//2))
227 |
228 | canvas = x.new_zeros((batch_size, self.x_dim, h, w))
229 | kl = 0
230 |
231 | for _ in range(self.T):
232 | # Reconstruction error
233 | epsilon = x - canvas
234 |
235 | # Infer posterior density from hidden state
236 | h_enc, c_enc = self.encoder(torch.cat([x, epsilon], dim=1), [h_enc, c_enc])
237 |
238 | # Prior distribution
239 | p_mu, p_log_std = torch.split(self.prior(h_dec), self.z_dim, dim=1)
240 | p_std = torch.exp(p_log_std)
241 | prior = Normal(p_mu, p_std)
242 |
243 | # Posterior distribution
244 | q_mu, q_log_std = torch.split(self.variational(h_enc), self.z_dim, dim=1)
245 | q_std = torch.exp(q_log_std)
246 | posterior = Normal(q_mu, q_std)
247 |
248 | # Sample from posterior
249 | z = posterior.rsample()
250 |
251 | canvas_next = self.read_head(canvas)
252 |
253 | # Send representation through decoder
254 | h_dec, c_dec = self.decoder(torch.cat([z, canvas_next], dim=1), [h_dec, c_dec])
255 |
256 | # Refine representation
257 | canvas = canvas + F.pixel_shuffle(self.write_head(h_dec), 2)
258 | kl += kl_divergence(posterior, prior)
259 |
260 | # Return the reconstruction and kl
261 | return [canvas, kl]
262 |
263 | def sample(self, x):
264 | """
265 | Sample from the prior to generate a new
266 | datapoint.
267 |
268 | :param x: tensor representing shape of sample
269 | """
270 | h, w = self.x_shape
271 | batch_size = x.size(0)
272 |
273 | h_dec = x.new_zeros((batch_size, self.h_dim, h//2, w//2))
274 | c_dec = x.new_zeros((batch_size, self.h_dim, h//2, w//2))
275 |
276 | canvas = x.new_zeros((batch_size, self.x_dim, h, w))
277 |
278 | for _ in range(self.T):
279 | p_mu, p_log_std = torch.split(self.prior(h_dec), self.z_dim, dim=1)
280 | p_std = torch.exp(p_log_std)
281 | z = Normal(p_mu, p_std).sample()
282 |
283 | canvas_next = self.read_head(canvas)
284 | h_dec, c_dec = self.decoder(torch.cat([z, canvas_next], dim=1), [h_dec, c_dec])
285 | canvas = canvas + F.pixel_shuffle(self.write_head(h_dec), 2)
286 |
287 | return canvas
288 |
--------------------------------------------------------------------------------
/mental-rotation.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 1,
6 | "metadata": {},
7 | "outputs": [],
8 | "source": [
9 | "import numpy as np\n",
10 | "import matplotlib.pyplot as plt\n",
11 | "%matplotlib inline"
12 | ]
13 | },
14 | {
15 | "cell_type": "markdown",
16 | "metadata": {},
17 | "source": [
18 | "# Mental rotation\n",
19 | "\n",
20 | "In this notebook we will show how we can enable a pretrained Generative Query Network (GQN) for the Shepard-Metzler mental rotation task. The problem is well studied in psychology to asses spatial intelligence. Mental rotation is a congitive hard problem as it typically requires the employment of both the ventral and dorsal visual streams for recognition and spatial reasoning respectively. Additionally, a certain degree of metacognition is required to reason about uncertainty.\n",
21 | "\n",
22 | "It turns out that the GQN is capable of this, as we will see in this notebook.\n",
23 | "\n",
24 | "\n",
25 | "Note: \n",
26 | "This model has only been trained on around 10% of the data for $2 \\times 10^5$ iterations instead of the $2 \\times 10^6$ described in the original paper. This means that the reconstructions are quite bad and the samples are even worse. Consequently, this notebook is just a proof of concept that the model approximately works. If you have the computational means to fully train the model, then please feel free to make a pull request with the trained model, this will help me a lot.\n",
27 | "
\n",
28 | "\n",
29 | "You can download the pretrained model weights from here: [https://github.com/wohlert/generative-query-network-pytorch/releases/tag/0.1](https://github.com/wohlert/generative-query-network-pytorch/releases/download/0.1/model-checkpoint.pth)."
30 | ]
31 | },
32 | {
33 | "cell_type": "code",
34 | "execution_count": 35,
35 | "metadata": {},
36 | "outputs": [],
37 | "source": [
38 | "import torch\n",
39 | "import torch.nn as nn\n",
40 | " \n",
41 | "# Load dataset\n",
42 | "from shepardmetzler import ShepardMetzler\n",
43 | "from torch.utils.data import DataLoader\n",
44 | "\n",
45 | "dataset = ShepardMetzler(\"/data/shepard_metzler_5_parts/\") ## <= Choose your data location\n",
46 | "loader = DataLoader(dataset, batch_size=1, shuffle=True)"
47 | ]
48 | },
49 | {
50 | "cell_type": "code",
51 | "execution_count": 36,
52 | "metadata": {},
53 | "outputs": [
54 | {
55 | "data": {
56 | "text/plain": [
57 | "GenerativeQueryNetwork(\n",
58 | " (generator): GeneratorNetwork(\n",
59 | " (inference_core): Conv2dLSTMCell(\n",
60 | " (forget): Conv2d(394, 128, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))\n",
61 | " (input): Conv2d(394, 128, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))\n",
62 | " (output): Conv2d(394, 128, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))\n",
63 | " (state): Conv2d(394, 128, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))\n",
64 | " (transform): Conv2d(128, 394, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))\n",
65 | " )\n",
66 | " (generator_core): Conv2dLSTMCell(\n",
67 | " (forget): Conv2d(327, 128, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))\n",
68 | " (input): Conv2d(327, 128, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))\n",
69 | " (output): Conv2d(327, 128, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))\n",
70 | " (state): Conv2d(327, 128, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))\n",
71 | " (transform): Conv2d(128, 327, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))\n",
72 | " )\n",
73 | " (posterior_density): Conv2d(128, 128, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))\n",
74 | " (prior_density): Conv2d(128, 128, kernel_size=(5, 5), stride=(1, 1), padding=(2, 2))\n",
75 | " (observation_density): Conv2d(128, 3, kernel_size=(1, 1), stride=(1, 1))\n",
76 | " (upsample): ConvTranspose2d(128, 128, kernel_size=(4, 4), stride=(4, 4), bias=False)\n",
77 | " (downsample): Conv2d(3, 3, kernel_size=(4, 4), stride=(4, 4), bias=False)\n",
78 | " )\n",
79 | " (representation): TowerRepresentation(\n",
80 | " (conv1): Conv2d(3, 256, kernel_size=(2, 2), stride=(2, 2))\n",
81 | " (conv2): Conv2d(256, 256, kernel_size=(2, 2), stride=(2, 2))\n",
82 | " (conv3): Conv2d(256, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))\n",
83 | " (conv4): Conv2d(128, 256, kernel_size=(2, 2), stride=(2, 2))\n",
84 | " (conv5): Conv2d(263, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))\n",
85 | " (conv6): Conv2d(263, 128, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))\n",
86 | " (conv7): Conv2d(128, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))\n",
87 | " (conv8): Conv2d(256, 256, kernel_size=(1, 1), stride=(1, 1))\n",
88 | " (avgpool): AvgPool2d(kernel_size=16, stride=16, padding=0)\n",
89 | " )\n",
90 | ")"
91 | ]
92 | },
93 | "execution_count": 36,
94 | "metadata": {},
95 | "output_type": "execute_result"
96 | }
97 | ],
98 | "source": [
99 | "from gqn import GenerativeQueryNetwork, partition\n",
100 | "\n",
101 | "# Load model parameters onto CPU\n",
102 | "state_dict = torch.load(\"./model-checkpoint.pth\", map_location=\"cpu\") ## <= Choose your model location\n",
103 | "\n",
104 | "# Initialise new model with the settings of the trained one\n",
105 | "model_settings = dict(x_dim=3, v_dim=7, r_dim=256, h_dim=128, z_dim=64, L=8)\n",
106 | "model = GenerativeQueryNetwork(**model_settings)\n",
107 | "\n",
108 | "# Load trained parameters, un-dataparallel if needed\n",
109 | "if True in [\"module\" in m for m in list(state_dict.keys())]:\n",
110 | " model = nn.DataParallel(model)\n",
111 | " model.load_state_dict(state_dict)\n",
112 | " model = model.module\n",
113 | "else:\n",
114 | " model.load_state_dict(state_dict)\n",
115 | " \n",
116 | "model"
117 | ]
118 | },
119 | {
120 | "cell_type": "markdown",
121 | "metadata": {},
122 | "source": [
123 | "We load a batch of a single image containing a single object seen from 15 different viewpoints. We describe the whole set of image, viewpoint pairs by $\\{x_i, v_i \\}_{i=1}^{n}$. Whereafter we seperate this set into a context set $\\{x_i, v_i \\}_{i=1}^{m}$ of $m$ random elements and a query set $\\{x^q, v^q \\}$, which contains just a single element."
124 | ]
125 | },
126 | {
127 | "cell_type": "code",
128 | "execution_count": 184,
129 | "metadata": {},
130 | "outputs": [],
131 | "source": [
132 | "def deterministic_partition(images, viewpoints, indices):\n",
133 | " \"\"\"\n",
134 | " Partition batch into context and query sets.\n",
135 | " :param images\n",
136 | " :param viewpoints\n",
137 | " :return: context images, context viewpoint, query image, query viewpoint\n",
138 | " \"\"\"\n",
139 | " # Maximum number of context points to use\n",
140 | " _, b, m, *x_dims = images.shape\n",
141 | " _, b, m, *v_dims = viewpoints.shape\n",
142 | "\n",
143 | " # \"Squeeze\" the batch dimension\n",
144 | " images = images.view((-1, m, *x_dims))\n",
145 | " viewpoints = viewpoints.view((-1, m, *v_dims))\n",
146 | "\n",
147 | " # Partition into context and query sets\n",
148 | " context_idx, query_idx = indices[:-1], indices[-1]\n",
149 | "\n",
150 | " x, v = images[:, context_idx], viewpoints[:, context_idx]\n",
151 | " x_q, v_q = images[:, query_idx], viewpoints[:, query_idx]\n",
152 | "\n",
153 | " return x, v, x_q, v_q"
154 | ]
155 | },
156 | {
157 | "cell_type": "code",
158 | "execution_count": 186,
159 | "metadata": {},
160 | "outputs": [
161 | {
162 | "data": {
163 | "image/png": "iVBORw0KGgoAAAANSUhEUgAABH4AAABuCAYAAABRLNSRAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzsvXmYZUlZ5/+JiLPcJTOrsrZe6YZmEZABh7YVFByaQXBBQWQQGlBQBzdQR0AF0eQiKnSjzAMuqCgiDYIywiiigLIIgiL6E3FEFmmaXuiuNde7nHMi3t8fcc65597MKrLoqu46RXyeJ6vy3nuWe96MeOONb7wRoUSEQCAQCAQCgUAgEAgEAoHA+Ye+q79AIBAIBAKBQCAQCAQCgUDg7BCEn0AgEAgEAoFAIBAIBAKB85Qg/AQCgUAgEAgEAoFAIBAInKcE4ScQCAQCgUAgEAgEAoFA4DwlCD+BQCAQCAQCgUAgEAgEAucpQfgJBAKBQCAQCAQCgUAgEDhPCcJPIBBoLYPBQAaDwb3u6u/RFoK9dk+wVSBw1xPq4e4Jtto9wVaBQKBNnCmfFZ2JL3OmUQN1DfBTwH2BDeBfgF+SFfnQHbjmHwA3y4q86Ax8v2cAPygr8rA7eq0zQbDXHUTxDOC5wD2BdeBPgRcgrN2VX+uuZDAYCHDvlZWVzzbeezFwr5WVlafdZV/sHCXYa/cEW50ewb+f1ncJttoloR7unmCr3RNsdXoEn3Va3yXYavffJdhql3yl+axzLuNHDdRPAf8b+GXgAuAy4DeBx92V3+tcJdjrDqJ4LvBy4PnAHuAhwN2Bd6OIz/C9zkmhNRAInJsE/757gq0CgUCbCD5r9wRb7Z5gq8CpOKc6omqg9gAvAZ4pK/KnjY/+HPhzNVApvpP+pPL9PwZ+RlZkogbqEcD1wCuBnwEs8EJZkdepgXoW8FRA1ED9JPA+WZHvUAN1MfBq4JuATeCVsiKvKr/LO4FPyoo8t3z9ZmAIXAe8BojVQG0ChazI3rNkklMS7HUHUSwBA+D7Ef6qfPfzKJ4E3ABcg+Jq4GaEF5XnPAK4HuHS8vU2myC8qvzsxcADgDHwncC1KF4I3A3hWHnMg4F3ARcj5Gf3gc8cg8HgEexQflZWVl5Xfv5+4PqVlZXXlq+fAfzgysrKwwaDgQJ+DV/GOsCNwFNWVlb+bTAYpMAv4ctsCrwN+F8rKyuj8jrPx49iCHCHRx3uLIK9dk+wlSf4990TbHXmCfVw9wRb7Z5gK0/wWbsn2Gr3BFudec43n3WuZfw8FG+Yt53k85/DZ2R8DfAg4OuYNcaF+KyNS4AfAH5DDdSyrMjvAG8ErpUVWSgLq8ZXhI+Xx/934CfVQD2mvNb3A09XA/VINVBPLe/1E7IinwR+GPhIea27srAGe90xvgFvvz+deVfYBN4JPPqUZyt2tAmKxzSOehzwVmAv8KvA+5k6XICnA29uk+jTYFv5GQwGy7s479H4RuI+5flPglIIg5eV738NcK/y2r8AMBgMvgV4HvDNwL2BR52pB7mTCPbaPcFWwb+fDsFWZ4dQD3dPsNXuCbYKPut0CLbaPcFWZ4fzxmedUxk/wH7gqKxIcZLPnwo8R1bkMIAaqAHw28DPl5/nwEvK899ZKolfBfz9Dte6CjgoK/KS8vXn1ED9LvBk4F2yIrepgfoR4PVAF3i8rMjGHX/EM0qw1x3jAHAUYSf7fRF4MHDrKc6/CjiIUNsERW2T8r2PILy9/H2E4vXAjwO/hcIAT8FnA7WRHHjJyspKAbxzMBicqvzMn7eIn3v80ZWVlU8ClMr4s4AHrqysHC/f+2XgTcAL8A7zdSsrK/9WfvZivP3aQrDX7gm2Cv79dAi2OjuEerh7gq12T7BV8FmnQ7DV7gm2OjucNz7rXBN+jgEH1EBFJym0F+PTpCpuLN+rz587bwgsnORelwMXq4FabbxngA82Xv85PoXtU3IHFsQ6iwR73TGOAgdQRDuIPxeVn5+Ky4GLUZzKJjfNnfN/gdeguAfeaawhfPT0v/pZx8K2NY5imMlMOlY6wYpTlZ+alZWV9w4Gg18HfgO4fDAY/Cle2e4APeCfBoNBdbjC2xR82f2nxqWaZfuuJthr9wRb7Y7g33dPsNXpE+rh7gm22j3BVrsj+KzdE2y1e4KtTp+vKJ91rgk/HwEmwOPx02PmuRVf0P5f+foyTp2R0UTmXt8E3CArcu9TnPNLwCeBe6iBeoqsyB+d5Fp3FcFed4zKfk/Az3P1KBaAb8WnPz4IXzkrLmz8fhNwA8KpbCJzr8Yo/hh4Gl4BfsOX//XPKl/AL3L9ycZ79wA+vcvztzi53VhZWXkV8KrBYHAIb/vnAyvACPjqlZWVW3a45heBuzVeX7bL73JnEOy1e4Ktdkfw77sn2Or0CfVw9wRb7Z5gq90RfNbuCbbaPcFWp89XlM86p4QfWZE1NVC/gJ9TWADvxitujwKuBv4IeJEaqH/EF5pfwC+4tBtuB65ovP4osKEG6meAVwEZcD+gKyvyj2qgvgl4Jr7jfwXwNjVQfysrckt5rUvVQCWyItkde+ovn2CvO4iwhmIAvBrFOvA3+DmWv4nP9nkj3m7PRfFSIAF+snGFjwIbKLbZBOEfT3HnPyx/DgEvPLMPdcZ4C/CiwWDwCXyj8EjgO/Dzh3fDvwBPGAwGr8Ur1z+ALwcMBoOr8OuL/TPeYY4Bt7Ky4gaDwe8CrxwMBs9eWVk5PBgMLgEesLKy8i68w3zdYDD4Q+DzeMd5rhDstXuCrXZB8O+7J9jqyyLUw90TbLV7gq12QfBZuyfYavcEW31ZfEX5rHNtcWdkRX4Vv4r1i4AjeEXx2cDbgZcCHwP+FfgE3pAv3eWlfw+4vxqoVTVQb5cVscBj8Ysq3YDv6L8W2KMGagnfMX+2rMgtsiIfLM9/nRooBbwXr5bepgbqS00HOqsEe91BhGvx4ssrgA38s/WARyFs4TNyPo6veO/GO4jq3JPa5Evc8+8AB/wzck6kHO/ES4APAx8CTgDXAk+t5pvuglfiG4Hb8fN739j4bAn43fK6N+JTU68rP/sZ4LPA3w8Gg3Xgr/FT4lhZWflL/BaV7y2Pee+X+Wxng2Cv3RNstUuCf989wVanTaiHuyfYavcEW+2S4LN2T7DV7gm2Om2+onyWEjmXsq0CgbsYxTPxTuAbEb5wFu/zXuBNCK89a/cIBAKBQCAQCAQCgcBXPEH4CQTmUTwdyBHefJaufxXwHuBuCG1d4T4QCAQCgUAgEAgEAi0gCD+BwJ2J38798cBPIPzBXfxtAoFAIBAIBAKBQCBwnhOEn0AgEAgEAoFAIBAIBAKB85RzbnHnQCAQCAQCgUAgEAgEAoHAmSEIP4FAIBAIBAKBQCAQCAQC5ynRnXkzpdRX7LwyEVGnc3yw1e4Jtjo9gr12T7DV7gm22j3BVqdHsNfuCbbaPcFWuyfY6vQI9to9wVa7J9hq9wRb7UzI+AkEAoFAIBAIBAKBQCAQOE8Jwk8gEAgEAoFAIBAIBAKBwHlKEH4CgUAgEAgEAoFAIBAIBM5TgvATCAQCgUAgEAgEAoFAIHCeEoSfQCAQCAQCgUAgEAgEAoHzlCD8BAKBQCAQCAQCgUAgEAicpwThJxAIBAKBQCAQCAQCgUDgPCUIP4FAIBAIBAKBQCAQCAQC5ylB+AkEAoFAIBAIBAKBQCAQOE8Jwk8gEAgEAoFAIBAIBAKBwHlKEH4CgUAgEAgEAoFAIBAIBM5TgvATCAQCgUAgEAgEAoFAIHCeEoSfQCAQCAQCgUAgEAgEAoHzlCD8BAKBQCAQCAQCgUAgEAicp0R39Rc4PSqdygGgGp9I9Ytqvmig5g88Naq+nzud084dTva8J7XD9FlnjmscuxsTnsz8bWLmGXZjB3WKz3a6+CkPaAFf8hk0KPcljtnlpVteoE759WfK1g4a/JwNp9dqHut29oNtZq4QqLmPt9VN2X7Ol7w2zNnczR/ZEuafofTjJzUamPJ/O9eent+Uz1rXqR2evapgdUXbnX1a7qK2M/9AJ6mPX/KZd+OYzjvndWpmfPhObeQ2/3Q+1c2Gb9rxb+3r29QEbpuvV+UbJwtrK74CitIp20k53fj/fKqHzfI187xzMZZyu3zWxnnKtb9ezv2tpyaabyPnzjmd5/6KqZBzMcKugoGG76+QL7/P9OXQIuFHMx/kVgGsALYqaIra+FppnANU9ddw2xpWVV5LqnPxjYsu7+fPdDhaVHYVbGtk5ysiGtV8btmhw6B0o1Hx9hZ26DDM2c01G+w2MBdUGAwW6xvPmYrsy0MMgCNXCqk8Z9mR0KVNLPPnMi2bUJc9aVsDUpctpo6q2biK9uVGQS3Q1sHatOHYKf5QzLpRadTpkwV85zLV8zSfZeY5muVL9PwZNOujr1vg0NMGukSX4o+Un1e0rWwptP/OjcLRLBMG/3wW5+2pKW03c5HyPF1eYlrepFn/lAan5wpUi+xV+2ldPphMX4Ovm423tQax/vO49M9CVHtqNffsTYGx+mzaVpzphznbaKZyl5u+pxTbhJ+GfwZTVli3Yxta1eWpV9OlaU7VuT3HadhASeNvzvQ9b0lNUb/bqGOnaBtmPq9sVLUVrqU2O5lfn6fhyxwaUc1Af85mtY3mbNW4VvtoxO9qGhcofAzl7eZ9mUbqomArMVsB4mbjA6jtomW2+LiqLt6Jnakzzm5EmvJ1FR/UdpsXr09aH5nze7SyHtZfX+EbO1c+bxUjQBmbzp/ofbs6yTNP28FGEHoqgeRcp45/VB2UVuWmqOpZFbs3xbMy7vcmKOMvpVDOH9SMb3csU9BSwazxty7r06wrrsqUAuyp24O6Pu4wCKXmfP1ZLlMtmurlGj+eGdvsMOrr674GEVAOI7AosCyaZYnZg6GHJmn8Mau/oasv1baCWjH93gp2qMTzog/MFodGp0hVHYXGtavrNCq4nv7aKqpGs/oR7GyFVYAxKD21j0KV5apxzMxFp++p+feB+bLcGmqRomTbc5/MpTRtN3+O/zmVr2tT27ojXyp4q0NZW/7MBhXbnr/ZsJboul47tGljTWwEpw2f4mY+dbMCzo54cWzaKM9RBTbKtdNh0YhBaxrt4/xoktKI9YJ1F9gLPPii+5AiKIRIm5nDp4Hb/HXO2Ne/86nKTGSmzyZ2LiidP6cSfeb8XcMOzZZzW/vX1gYRdm67ZMdfp/57Jh6Ytef0Or58zsQkO160pZwsaJ8xpNvhvZ2O24EdB/HagdJ6qn5VfZ9KeDbz9c/54dYdfP22eEo1hCBmf/+KYK5e1l57p5h07vgZqphhJ1/YAurHcju8KfMfTImAWCBFs4BmLxFLaGK8hjR3deo2tq2FrHS+KvJ5Hz5q2MGpbOvjTfuB2pT9nyYyl5zRLG9ttRUw66+n/bZZkV9O7pdL+9Uy27xPq687vdTZpkUZP8BcQ2BlGgD7AYFpGDbv45RAH7iIlEViDDBBWKVgvTwuk2lHQJQrRxvmLtQyTCWCwbQTqWgMgDbVxuqYuekDZQBrm8c0OwVlsKOmd2oNVRxC006AMQpbydcOKHwGkNYaHJU0tA3bfLHTIY3y2sztaBMKENFlGSrrjMM7fqPBTp3jtB6eRO1vOkHl6/TJAmfhJJ+do2wLwgSkzBdD5VO7AVUwEUljxA4wJsHaArTCOfF21Hg7uwKlNS73I6FFdR8FVmZKYivYKaPE1w9d1qu5joDdYapWFXyoGae0fZCgeU6bxj8odWh83FW3UXVn2pXlDBAwOsZZX/v6aPo4HtL9KoarGQvkRMowdMXsQO9MYOJ8XS9/byWqUW5sGbAbBw4iDNZJ1f2EcgTTDxpXOS1VmZrLipoeXjaRDo2eZsRW93Tt7CTUGsOcTmEpB8Tmg1eFV5+dTM9RvkgaAAOF9hfQ4jOyc+fKTr+p8j5oVTmbG9mts8Bktm2v2vu63ZcCqQYmt02zdzP9iLrdq8S4kw0GnOOIOG+YkiSFYlI+h/XCkEiBw/kMRaE0mqsDqzL/Z5ufqtuIuUzH8sN2cyqhb1tbydRAxtSdc50YnLWzYyvK/1TJMRSCEo3C1IMsbaHODif2cxmkoMpaUaqqYY5pBvBUuIjwok+3TAR48ML9mUSOD67+O6sux1CUMe9sJr/B10XvD1uGBikyPyhkVGmK8u/tmnHRtD4pcbWdnfMOSpWZxKYhJdjqvKrdm/dlrWJ7O+f9cemJpOwfGwFRqELqmTGuikEbOgUwraS1r5oO8tbiEJzVpJN2CT87OEDfHs4qjar2/I5FYhZQ9MWxSMQrHvtz9DYV2jlGkePYQs4L/uw6ciBn2mDPBL9tK60zUfwsdUCybTRgLu0YV06taDTA0viBbfaxtK0L5anSjauGUwHWTr2VwivcosBZR16eN51hodk2VW7GNnOBXdvK0zYa2SiqFHp0AlEMKi57pt6xiYrBpeUzD6FYRVwj+tiJUwU6JxtRPYepv24VPTTUiDqIrwSb5rFV5SuPMdogCqwBJAfEB9NlA1yXsvbEa7PsMEIpTSG62YGXufO2BRd2W0ddyU5Fx8393w6moqKbdjjrQYuqk6nBWpIyqE2xPHjpPnQmXUzU478u35v/78RnyJl2qJzaoW04H1DiC5MDE00FZm0irLMoZRFtvP8CnMtRxiF2rrjNiLVTW1mpxlLaKSbOsMPgROPt2ePmYyRtwBVobXDW1U2iMZrM+iuZCEyhEOe8TmR96VNKIa0TrOenae3wl1d10as/L/WvnanKZqP77TsbswJsq5pCVXqYShg0kGX+oyiJKXKHUoKJNFoJWSGoWCOFmymA24aPTmaANmdk7IZGHW28nC181pcwnSa4LKvHd+MYihxMZMjz8hgNriyQSqnW2k4JM8KhMO2/+NArAjTGOVIgRbGI5r77r2BRYjpjzeJIMYwNCULCtLxVAy47LuPQFua1de0HEL1T0qBSUD1QHUB5QcONwGVIIaXQ4UBNvLZTCbLiBz3c/H0acVkr2ZZB0vhfmMakDsCglUFEsMQgF5bK2FG0HmNd4RMKynpZ96XV7KXvDNol/MCMddRcQ1BlnCitveIrsEDOWx//ixw8qjGFo3tEERUQ2ZiRLjhkDXdDs4FlBEhlEimzFoR2ltyyoM6IPGUnSouvsDIzNaCRtK6KmWvUFyqnfxkAcT54VuX75RSMem5xS5yiMM3ekVLcqmZw+XnjpShkBW1MebSGSHkjOh/Gbesc1I5BlyPmelqmmHbcWmKmOdxUqC6TKySKoH8B0AEdgzM87vffzHEbY/KEbjHkQnWM1z3jamA0e7nTMUKrDNYYza2F1bJu1dpZQ/kHpB4u8NoZNieONK6wiFgfdBim1dX6jlRRXrY5stAqU1H2zStfVQnNdSVRzCyAB8wvtOhN4uuYhe0jLQ1M6QvbWAdrP9v06wKIRnTpX1xEBCgcXSyLCA9auBeLE8WqXiTLC/q548ruffjo6LNohKxOFfJMMwvaJYptQyiVHki0wRYWBURxTJb73/tph80CWDjog7WtI2VHoUDLDmv8SVT6+dKn6/oW5YGu8Xe5Mx7yDNEYNKqSgmuRoqE7mMbxlYBhBOwkq4UOhfbCNFC4CK0cSIHLqhuVGVOlHWX6dvtQpR9qxl1QdjSZjhTjM8lVWV9PJhDOJN1Vb1THSkvro9bTjLtylqXWmiLzIr1zPn+xErGlmA4wVeWtKUY2Z5rUrnCn8tPmTvp8R5Pp/9u6JY1jlYNYQybgJl5hUxZiBTbzl8itw8QaWzhfXzWIOGyVLdM2BKQc8Cn74T44LcQPlmG8qFHERFi+8YKv4pKJJh5lsJ7TjTQyzuioGCeO+6WX8vHJTWxgsY1sPsAP0tWDUu2xle/X6NJvl+k6dYVykHR56ps/wJF4H1GUkG2ssT+xvOUZT4FiDPkGZJulkp3VF51mH58kQwbaVwdnYiwfTfkBV2jMVfWPXPlyHWFFQ7TIw5/yh6jC8bd/9Fys+wJEG1g7bKQsRmWMOl0tr2ojzjbtE35K9RaoU60rY1WLUDrn0JEvjYtWc+AE3PNEF+cKlM4xxoDTLIqibywvf8wL+O53vbS8TiW/NUZy2lZg0VQLpcrMqHcVaNTLqFKnbNedKGoTOGGHc0tFvXqvXjCtIRi1jHrBSQ3VIpOR1qjC4RNffRpx7hQ6TnH5xEe7Rp08xWKukdj2mpMEKS0iMr7xi6OIjIhn/MYbOEKfhajLZtTj5vQAI9OBCRzUBeubUo4Is71OzY0MVH39+c/aabJS9Csbkm3iTCVe6ObxfhQlAdLClZ14TY6jyLwJk/LozEFiDJn10xGr67dR1Gh2PCtUmY9yqgCiuUpN3Xmg2Vctz5dqNnvLpy81qYKI6ncFSsUocfSBKw9dQXfTsuC62GiB/9wyWOC+ixeSuFXuv+de/PvaZwFFBhR1x9LbqP2LO1M7EOvKvFQdk1sNJkaSLpvaQNrjab99PeJy3vgjT4PhMVDjqVg7T7XC+E6L3EN7i5bM/DfNgJ6jWRSqGFnpBMEgcd+fqTLQCpuXU1y1A5djtfYdB5nsWOfbw2xHZ16r9pS9H1UFr9WS6nMi9tx1TmaO1prL+cFYVQsUBicK4mj6UDpCrPMqRVk25pLsSsrBttKfN715nVTbskHI02H+macVEC+A6JgMDUmVs6JxAhPr/KBlHIG1WJdBDJJP/HU1PiO7jTZToBDQuuz3aKALcbmuW9zlwqsewUIRcdkoI7nhiywMhYUixjpB2QJnEsbOYLVmURd0JorN8vJNHa66Xxvt5MtOuQmPKxdhECCJwXQ50jnAbf0LyDPoHdhPYTO+9Y1/TcdtcbfjX+BVP/AkkMxHo3baSiil2miOXTLfADYEvyoxihTrUogPgDvIhr0vyhU85ntfzrv+8PlQ/CeY4dSh1RV3fqpv+f9ZNGaLhB/dGA4vaifXbEBnOgZOiGJwVhgzARMRxRFYjS1yjIkRsexxCYuFBRTVv3WjrQAXMf2jtCeS8zMNDVQTk8SgEBzTdQvmO9czI5WcpNxp50cFaBxb/11onzNsNpiNIK4ofCpoF0OEUAC5OFxRTPM9rfi0oFp8LMUx19ixS/mfmSk91X2hXbZiNuCw1gcKWeZgaR+H9V5WF+/GuopwKgYVoSaQaCAfEVf57s1nLstddd2q+MwfNhPYnc0HPKN4715XifJZmzsgGBrZBJXwKr6zrVVCJMJBoEcVviWl8GqJsFg0x4ANqxAMuQiqtmRjkegWUK8DVfmi0nC6yuJRUWmjojSYr29Gpja2M9N+C1wVCCsHEqHKGdiOYrv/axOiG5kXfiFUoRLvdSnNa752+V4sr1u6hWGiU450D3Cb7qCU4mMbR7lizx4Wi5wr+1fw8a0b2CrLS4Gmmq1erfgws3Nmm+zVcFpKDBbjp6BGCxAvQLSHJ73+T1jVi9wUJyT5Ftf81lt40w89GYZHcWzuIDoWVCN29fuqMeVXYHZnufbUw7oubYsNpgc0ZkLXcZgVjZhFiHrQ2cPTf/t3eMOPfp+fV9Jb8hdUCmwBsYViHSaH/edFS4XY+YQdPVc1pMCPFtPoOeo6JtiWTdeoY3Zu8Lw5raBuT9qCMBVIq1hILJgYlAHTgWgfqBjsBGQE+eFadN22C1oj3ASY2Ul2W7rUecTcANm2eMj5uEI6eyHq+iwrXXXz5rt7BeRDsFugwbgca1tW/xoYA64QxBpQHTBdLnr4tzOO+zijGOWODbOA0hPWhkeJ05jR1pBemeHktGZNNJOFQ6zZCdYNiYGIqBwMcdPlHWpxsV0imf/q0/VrNQbtfHsouYK4Q2q6aAvdHuQZrNqELE1YKxbpx2u+zczXcVZI0pR8PClngYhf76jOaGFmVk67M4fn+7du5rXFIcQQXQr53fj6J7+YkVsgjuDY+O4s3fvxrH/m98CtNnx8AaLr/kC1Hu+dMZWwRcKPV3OlIUyc3DAxziVkNmILYWtk0UbjsglaxxjtxRyjfAQTF37J1SqILme9ljdtiD4tquDTglk2mFaYDap2qIRV1o/MiV31aIzxjbSUq0K4xjnQ3tGVZsRQihMJsIeUBy7fg+9/9BP5tbf8Khtoxq4gcg6HJQduIvUjCtV1nAXnyhT3aSeg6ooXM6JHu9JEYSrK1K8ddJIu40wo0j2coEtSBhrO+fnkNrNkwChZBKLZC1QCbqkJGXaI2drW0Www/dqNjs3cs0zXe6jmWBtEaazETETzw094FntzyMSinaOvIMoyOpKRUXCim3Dtn/8O61gmKMZIOxccBGZGP1xUZpu47bVkpkzoMpiJgCXfeZAcGCGMZjpTiB/rqhvXNlJPEfFG8I9R9RKNX29Ld7jfV1+F+tztxC5iolPWkj38x5qwke5HKcFGEf+59kUetLBERyz32X8Fnzj2GQqYbtWtGpmf7SxQUxQU1kKUQnKQH/6dN7IR9zhmFrm1fzdOuAjrhJ4xqN6FkOyHyRZih8xPK/S2LjMYZoR/NW0PG3+f1pruZOJPEwGDpgNsmX1818tfzRf7y9y+eCHf8rv/h4UkIc8UkTJ+zSQDmWTsLY7yhmd8G1g/OKVbuKjsNptUQbzzu+glaPyqIt6TWfECtwLWVAxRWZfrbA2FFxQd6AnicqZTu9z02J3ufa7THFDUEUR9LxKqLt/9i9eSRXuxJIjLWJIhb3nBs6AYIw72yAjEd1eryRY+CtO+E3syXy6tDh+mNAbIKrZnlvk3UmCc7Of7fu8NjJMOmdIop8ApjDFY57Da0SnGHLQb/PozngJk2MbmNm0zmNLlQKRSIAZUlyse/m0cNUusk4IoVBKRO4PKc0y8h5E9xjjpc0wnWKXJJGcS9/nk2ghBc6Db4+7L9+HYic9Mb1QPODErZraIatqaUqDEL10hoiDu8T9/+3XcaAUVQZGVrieGjQJEGUZx7FP9nV/jIZv4TLFq0E6ala38v30WKplXVCsUU5/sAJUiah/IQa6+5ufZtJfh5N4oScmdAIe4/5WP5+8/8x6QLYysosh9jN4oP1WPUVUDxGfx0Vok/JQjmo2UgEin2HIRRld7wRRYALUHimWGCONhRGYLpHBEkvmUNO1wGgqbYScZiwiLCEOqdWoaa3PsnGt6DtP43lUMapzfXUNXq+B1AAAgAElEQVQxs8lIXciqfoQBrEKh0WX4702rQXd91EYOkqO0RfKsvJ9q5W4TqsookEbFQ9ND89Dlr+KiNcODbkl4+0N+AWs0VizKCZPIsd4Vrvqb34Oeb1iwORRrYIcgXgCqsn+8oOHQUm3YHZd3q5ZWbQ/NjJVIaSTLYDECJ2jR5BMLWiGRYmytX0TQdhmiQae1uONHicHvQy7165lB1PJeto0B3PzI49yggZTptvVnOoZ4L5gFMD2e8cJfprjhFo5v5EzIEBG6WU4yyujbCUt2hNIFqVU8ons/ji9YPnzk38jrmttWIh+oEWEQLONpR7vZ8Snrra3fWwC5FKQLrPofyf3IigYQtM3RarouiSoDufaNRnkj2HLHEb8ep/aiRrRA72u/gWO5oZ8OoYj59DBmLeszVB0KFqDIGeoCHe3js5u3c9FSH4oRKTABlBJE5fit4KuMBVXqcu3KJPPZUWV7bhxECU/9w7/ic50LmUTgkpT1XHz+nNFMVMwttsu3vfaPeefTvwWKE1S7pc0MCJXlsNqoyDayaWcTuFtkK+Z8bB0oTN+aXzfLy60Rizge89Lf4rPpQcaqS+GWoLPEYRSqa9AC/TShsBPGYpGxBpdCvln6xJaVK2iIsHG5dsOERAl9FAtoljF0S9lHgLzMtFY4/tkchG63vJCe/i8aZAxuBPk62hSQj8vNdlpmnwaKqMwijCHaw3e//DWsp/uwqsthk1IogxWHzQsKbfmel76JC7OCPesZ9/jE3/P6v7iOdRybwBbCJn61QNuMcyvz1EJJSzPJdmCHUGJ2UANFB0UPeOgvXMcN3YsYmZRCRUSNLdqdEpJU05us0ckiiHuQrZ80XmkD042RFOgUoj4bukMeGWIFSIGzFqtitI6QiaXIFlk1mv+3bhirLuDIxopJdAGp2mJrtMmBpIugaE531sb4Xa1maFH5Et+UV6JhjMXGGuIuG8kCG2KZ5NbveFkIdBU5PqMKk3vfJBajhSpBbJppXa0P28h2bWmZgmZb53YUWZVECBeA3I+HPOXnWHcXYvU+xCZsTRxRrMmyDBsv8A3XXMeH3/RiUj5Bh9vZQsjqjMayCwlEMu0Zni1ztUj4YU6NjiicDznELoDulIUtBXo8/JofZpwvc7+NnPWbbqBwGcZajDaMjOZYohgnCm0Ut3VG/NCTf5qffvO106lQlSc5n9JGtcbaHt5G4pVKKQMPKdNrZQTEiI78bsla+dEZnYLu88zrrmV0/Hbe/EsvQkYnMEqXi5zZaSZzy6jiBo3BIL7hvOB+9I8X7HeGC7cUy5nxK+UpL3DYWDge5/zs/76eTxxaIo5T1HidZbfF7//YD4BkUIwgG6LLEU2vV1Zdfd34aVGjUVF6JK3xqfvFhEQs6WTEUqHRkwwVg4kiJqOMOE3R2o8UCNNJEP6/qapTZRRtc3hlVlDr2GEErTkqIpR1K+pBvMTjXvZq1uhSxD1uHmouuNcFbK2toicZkVEUWc54dZMjN32ef3r3++iTU0QRPQtZV5HOZCS0LUuRGQdilPIp1v29kOdTxbESH2xOHWioveAu4iFP+Fms7tPTW3zgj38HL/6MyhGqIZajKNmi2rhkNiOrTfWwrCmqCuIiMB0uuurhZMkSY5dQFJpVWeKLw4yj+hAbugfKoJNFnHPkuTCkQNiib4SlyKJIoBQZvQruynW5yo6Da5ONGoiiXMAClGYY9zhuetgowgGFFoxSOOfICiHu7+fYGL7nt6/nLd/3CCiKsmiWnkuot4SfEUekFPihzvVpYxXc9p1l+kFzs4gURZ+IJRwv+66f5A1qifVoD1ZHpKpPYQxW6en04BgyHZM5YclsAck0Y23bvKlznWbmnQbnMFFEXOQsoXnZ9/w0h9ZiFiZgyvjIKlXb70/+x7fwmYP7kMJirSU2MQaDcwU9JiwXq/zmD12Dy05M3WLbClODOitO97ns6sfypx/8GNI7yNdf/e2+To6HLEeG/ZMJ+4ZjDriE9f+4kU6eco9Vxcsf8mzWEmGt41hNCl7+jtewimNDYOKYbWtrgzXLVAt91w5B9bYOaPl7pA3aFSySMDQ9hvFeJibFEtUdPad8u5FoUIlllG3i/yZqdlvetm2uV6EMKM2l3/gIxnTojCE1mjhz5dxJSzp0qBPC4ROWIzhuMxcyMl74QQsYQ+YMUb6Xwoxx5VwQbQzWWdx0+7OySLW7XLk6SSBikqQ4bVDK740dRYrMglWCokCVw9bgiLTyux9DIyO2mobZfsG16hcqdq4Odbslmm/6nuewwcWM8v1E6V4QhzKazAmd3hLxeEJnM+YZ//1ZfPRvfpbnPfF5/OxbX8E6igK/lEiVYHJntILtEn7AB2+RBpuCWwLuzkO++xdxySWMigyUIbeK43kfS5fjHGF1ISc78Tn2xhHOwVENn7n4Qm5KwDnHaMHy1n99J+v0iKIhSDENcE+V4nyu48CvUaTQFDgWgLsDS/5zWeJrH/88ConpRsf4yP95BUt8hnWTQncRogUec92rGJoOkvYZ5QU3Rpb96QFgEeIJOtuYptpWnfMW2avKvPCuTNFF+LrFe3BoyxHbwktBOsflDm1inNUorVBKsWgVw+4l3L6wn6Io0N19HI7gG//gb8mLLS4zQ956zaNx9gRU82orT+IszV2+2oMuV7D3GXgT5+hECkxBRzsuzguuODFmeSvHFBlaCSY2FM6RW8u7XY4zgrM+C8oojUN8RxOmZaiNCuI8lYpVp4Y2slVqYSaGaJnHvubPON47yKfX1zBxhNIJ62nMZpFzNHH0ignKWt7zjvewhHD52hoPWIiJNzNGxQjdMVQiyExmZFto2kX5KTSF5BB3QPeh12s8j/M7TGTHveiIA7mYR1zzEo6PL0fkIGOb8V++60qSSPtlRbSjb27gQ298FioaYQo/gmPLTKB679c2UO0kVdksSkAvsXzlw1mLuzAWDtmUztBw23iJTaVwpo9WHVwBihQtDh3vYZJZiBw3j1a5qNdnxALCBqhqbTio92xtM1VajgDieNuv/zIP+8kBmdrPGI0thCRRTKxFmZgsF7bocFt3P5jUi/iloGMwODRFYxGWOotMle5dQKp8+m2jw+cuzUyl+luLrrNVZ6aXiJdtlrD84mOfwyVHHb0sQrmoXm1diV+7QKupO7SqChb8zmhTd9+2trBaW6wa6XbgcnrAHuCiUYeL1wzLI00kPsJwpVCrRDMyl3BrepAiKdBApGOvJWYT9qixn7ai+xCPkUmBVoJrq/Ba+XUdg46wcYwho7Cb/MNfvgXSLtiCS9e2eER/mXttbqGzEUsqoTfUXD4CVyh6iWZvrtkXwbXf8myu/7t38Q8bn+GEFAyrezV6TtWYUhv5kk24ahwkYAtH4lekATRWVWu9lYcLoJRfL8kojMT837e9zft3rbdfuz1ua4qzoKCjOuiJoT9SLFtNbwuSYUE3y1HOsKE63MYCm/TA9IiUojCutIPCKc1Ed9lyFuigmUynwpVJAeXynq0yk5994JfysOLq/QlQ1tfLQiEWClcgJgatyJ1FGXAKbvr0Z/zgd+7IrPgBNAfbpqPWv5e0yUgNpr6jIWrV6zpV/bcR6+u3Ey3fEx0lbAxzFvuxjwMyhzjD8thx1dFjPLKved7X/xjjo8e4EE2OYgtVZxR7kensi9XtEX4U1AXKVauBLPLIJz6HNX1f1iYXkasMpTWx0Uxyh0kSxpFwg0352KUHiHC4TDixdw8nHvzVHFnqYZ0jTzKueuQDed9PfJyiuBlcY6KEzP3fFhoNntDFsRe4iKuf9EJGto+yjlGxyLrcHdEphbuNb7r62dz4vgHf8yu/xo37DrHVWeJWlbLhUuLuIhlDhkz8wi3xMkyOl3Nq3TR62yHD4VynuaaTQXMgWsCc2KQTpYiz2MJRRCmbUYexM0SdHltbW6RpnzWzyChdIlMWEWFNBNOPKGRCunUz6AShmG6HW9lIu+loQYtsNe+IlIaJE8hy3jp4Mc9/1s/T/bt/5ZN/9m6+81GPRokjd2MwCm0iIjumiH20b52g5remPVm6catsNIdQp77OCj8lusva4qUcTg5iOvsxyhHFMbYwTLJN3vWet0Ox6RdB7cdsKEeniLkschwyghaDcxmuTBtt27j5LNPyoDW4KOZ7X/snHI+W/a4b1m9rv0dn/NH/fKqfDhFpzFqfux9xLAPrziJxj1zFKBIy0ZAacr0BdMnLXdKmtLRwVXVFxSw++OFkepF+0WWxEJYOD4ncAp8bRWTxItDFRB1QCluA1hGFdIh7B5kMBVtY7PqEnP0UZEy3LYWqg+u7FJW42DKaXzgykG+QZhuM4z0UJiGONcOJJUpi4tyysDVmv3MsjoFck+BTry0OhUFhyh48WCxOvKhvDH6zKgDjs0Da1InaKePS9w2qVWpolDsv6vQw7JnA4jrEXkn106eVQ5QqtW+NU15olZkb+BH6anemtlEOW/gaomy9Vp2iw3iUkLslxpKgJas7DILvhA9ZZk16qFgwscJmvvwY3UHbiL7tQtqHzRMAtehjVOQ7oW0TyhRlBqFi7CxaK3ATdJKi3AhVCEvDTW7/0N+zb2MdYcIJDCkx93jA16O0JkLx4Y+8jzEFaziW9/SIfW2crrXVxoL05dCspFqD1zzoYjDlEgO6Lo+zJ4hAnuc88YlP5I1v/X3IrbdfPVB15z3GHUZRx1cKQBS9w2MWRoYDrkN3c4u9VpEMC3oToTAa149RdJmYBbJq+3dR5ZoCBmcNQxezOnRcdvAe3Hzk35hoixPfW6iSZMokjRaZazY6NFE5dhYnMBYu3bR0iow1rXF6wiiOOZGmjAEnwqGRwFqGilKUmvh2T5WiYj0drmonXL2UCLTJRlNmux+lY5GpsOWz90f8y1++lgc+dhm6HZb6lzMaCw5hb+RYPHGY+w6P8MhUuO+J4+wfF4zGEa/59hfynL+4jhuZsI7fia4Qh2CQslU5W7RH+AHqhk7wKX10GE9i6KWIKLRTaAXKFcQamORkovlip897nnAlh1NIXQcbxRxPhQ0t6E6HQgowBddc/w7e9PT/hpYMZ207S2oDr8UUwBJXP+nVrOWXc9QuoKI+ToEzEUr1yLMMrfaQqksYfOuA9/fuwxeTHhPtUGlKbA1SWPrdRcgSNlTM1S/9Vd73gqdgR6vEzg9q2rY2uLWC6/cPmozHLKkErFfHY93nhEu4ZeEAJzqLjDKFXriY2GjWJGK4OSZOIkQcIoJzRZkVA347W2YFsYaTbCPS2F1DrEYnhriw/Jejh7n3B9/PA48I3//VX4O74WbiSFO4HNECkeJCCm4uV7jWkcEVFkO1+KX4aYNN8afdU4QbC79WG47PPZCyoC1FUeASQBniToeJU8QaOiaGfAzZaGoXC7mzSKIYk5OaBKM0aL9+hC5v0z5msyy1A+c6rMYXcmu0nyT1c+0twuF8wsOv/1twFlGaZ7/u/dzzyBa3d4/y76u3c0z12VIJaWeBTVGs5gsU/TH/wBhtQFzkEzGquti2Oqm0H3nTMRd93SNYi5Ywo4SL1zTLxyYsDiGLhb7SZCYlUnuxxKiOgiLCiYCJyfMRunOIYqLYEkV3IWayOcEbZAzalpGtQ8jqDQ3bRJWtAmUbleWoccbf/NZr+Nrnv5hCJWgHSilGWcb+zHL/E+vcd3WLyzZX+Ts3YQtYVSCJxuYKRQrS9cKO3kCbAlsUWAdRDIWFOm+7TQZTjalc1QyA8uU236v8TpcWjRVFN+n4tkEVKARNjlNCbiKKamCl9GHT7kcKkgJ5lfDeGqbN1LR3IwomEnOcRQ4vXcyG20uadr0oVGbqOeU75BPpsqhgI88ZFzlODGmcIFqRZYVfVSLPQQs60rjcglRT61s4laLha7WKysxehcsmpHEHcY407bLlcrYoMGgmFGwx4m3/9gEmFFgiBEUGFHHKVp7V+1vWtmiIF7VY2SY7NWhqMDslQqsqQ9q5Uv7ye35GzhE7h2hvM63E73BZ4+MRJdWaUhqDpqjN1DJ7qSoLR9NHuN8JQ7wqpG5MgkI7IcKgI8iUQYlCIVjJsNVyFvSgAGMijOnior2Miw36RHQoyAq2/QFUy1QygXLjD9822bKuRCNLSsZDj2Tcbo8wSXo4o7gxifnkpRdxsyi00hy4cZ0LBNZyxxjtpzvjxzhsc6xIl/W8fHln7FR1pqkHQarvXS/4Uwlc1TrAQ5BP8a/veCkP/M4BRBGROUQmir3Dozx0/T/55jTjomOfZ08xpIfCbEbc/xbH6x/103zvX/8KnydnU6pr2pn7nA3aJfw0O89uDExAtijyLRb7BxhNUqwrKPKCxYUe2TjHRYaNzhKfPbCHW/almDwi1j4ALLC42FDkCV2tSCYF6B5OJ1BMaJ3zm0GDFsQJ0GXLXcIoug8Kg3OQlSvgGyxpmqJVBJt7uOmGT7Nm+0y6eyGyaCnoW0OaKzqZQ0mMSiPsJAYxWKNx1vqArmqZWlS5a+o5qgqjI6/sK82ElJuTiHF3Hy/88Lt4wEOegJi95CNNbCIMe9lfgC4gU1AswNAWRFGELhviGeZt0zZbzWR1lWmxuSWRjHuPMr7q6CqXHc1YWpvQS1KU89MdHI6JyzhIwbrAxERMbFF2NDTiGiO+bRUQT4KvEmXlED0dLhJAfOZAEhlskRGlBkFhHRS5I7UWpPCdKAdVa63rndMKcitIJEgh7TVd3ZmpRrXxaxrFPSbJHsbxEi7yQa5o77/Gkd8Vuj/MuceJMQ84scHB0YSLkyWGCxEb1gIT1qIOt/RSPjU5QkxB7sqpJ1JFzS1E8LnXqoMeRuxRsJxHHDpmObhh6OVdjmeKtDD0kg45CSKmDPIdURRTZAVEHZzVJP2LyLYgSVLShU1GYwP2CMgY2prl08BXN+ezfcRxADiytcXe9TV6XYi3hAURFiZj7ra2Qefv/pmLV4dcPBzz6u/4cX7mz1/BpgiZ7SJ6P1IsAHv51qddw19e/wqsOw5mDHZMkTMdCm4xzWlfFTNlQKoEeEWiYsYjPx1OygC5ipNVo8eqyteVCDK9WUP0bSPGgfMbaBT0OM4SHz4+RmUx2J7PfoL6OZXABz7yCQ5884PpLSeMtBfRCiVoJ5gkxrjYZ3Joh5vk5RJVVZzSMuZiwyiKcHkBkUZFgrUFRWbZGg4xqcEOhUIssTFYWzBSBVZpCufHwiOdsFlkTCIoMDjMzJTBKvNH5jOKW8JOdQ/mMpoExE5fa62Jne84Kpz/EXwnvJIoq6mGCuI45k/e+FZ/oSiCzGfmTatgS2w3o4g5EqC7NuHAuIe1lm6akE8mKAUFGqsFEYUhRUedcl2fBEWCOIPRGiMGiQuKbIHCbaLoYJTFqqyOGappdO1axa2xSHElwscJ+8Yxr3zSc+i/92OoqM8Ig8Oi9y6x78orOb68iLiC/cMtUnJiHFlDVi0qUWxOpaxnObc0MK0HQapsxUYGU7W+D6oAjgPwr392Hfd/7E/R2X8lF6wK91n7IlfHG1x+9AscMjk97ZCxpZN06eQCqxN+/dtfwI/+xbV8gQnrWIQddrE9w7RL+CkNbgQcE6L4Nj78jlfxDU99GMfHjkK8WpskEVluESOMnDBKljh+21HSPRdROEuGb0zFCEWRkcYJpoC80NDt43eaKIh1RGGz5q3bhVS1O0ZUVIo+jjhNUEg548hR2BwXCVuR5nh3gXixT6QNToR+HnPh0HDBluLQ0GCUcHtasG57QAJRBykUhSsamTPtQkmZKSvOizXOEakYIeYIMR8/uMivv+PdfNZcirrg3mSyl6JIUEpz83uPk3c0Sgo20iH3+rbLmEQRCHQ6CyBJOQLl59Uyl9LeQnP5bINyNM2UOWV9YtSxLRbHCiSjuxSRjTKMMkSiwDmSTpdrv/N5POfPruVWW2CT2Jc9HFobpLmWyA4CYhttVY8KUJTPFJWBe1H+vgBFnyIb0t277LdbzaHfgy3RPiDTPosMpVHKj3hOtsZIbkm078wr5YiUFxtdPc+zTfWxmkOtQRfl7gY+snXO+3Ytfp3hUtNGKVjYGPK1m1vst5aOFi5wY/qjMdYeI0pS8mHBancPabTFsfwoKTmFBmcLlDKItCkdo6SZpeQSLhumpMeGLOeO3iimX8R0CsOYlH30KIqUDRzKRFSPa4scYgNFgYm65PkIkiW2rCNZvNyvo7chYI8CY1DFNHGlNWXK40c5q7RsC2JJDx/nsqUFPvTyl/JDP/q/WFrVXL6RsfjRf+DyjU32jB29zNJ3cLt0uJAuh1kks8sg9+Nh1zyXsV3kSD7kvz35ZXzgzb8M9vN0EkWejXynTKq9nFrE3Nc96TSGMgCOiUmJME7T6y7UH1ulEQyRTdBO11qFcb7flJeZQVAO4DW3RW6JyQQoqhCrnPKgjWFcRMB+blm+lE25J7nsx6+N52PXaidRlY5Y7sCGBYWQdFO0Vqgc1ET5de+kALGoyP/qaWkWi6PMVBSyyYgk7pJbRRFBYYA0htgwGQ+xkuNQFLaou9c+gy5GBDJnccaQLvSxowhX7oGjyxv5NbaYTVdrSbnakfmOs0zf8h15vzB9XmWeoRE0TmmEqJyQWOFwTsid8LgnPI4/fttrQXKK5lTOtglm1YCaUeS2wCkhE0sUJ2QTR0pMJIoMRWQjIKUgxbkOkJbNaQRisRJhC4dWXQq9wOe3HJt0QTZr0Uca08s8bbJXUzxWOJvTYcR9j+dcdGyLTTX2cScZW7ccYfyF42w6v7jz0z/wEo4zKvuPFmXLS1Vj3KK9eFiWH5kZ5LwrnvUOsmOa3VxbVe0AzgboT/Hvf/Fi7vf4F/D1t/f41n6Pu63eyoU6R00mOBGiNPbO3BjSwnDPIx1+/9Ev4vve/SsUDBkr52Ots2iv9gg/jfRWv16KYO0asEa2eSsmOkjcXaKwYK0lTQxFriiSPdwWpYzcBn0tTMwYpxXdpOsXrXKGrPBtzjjp87Tf+BOuf+bjQN2KsxtTxa/+Dm2hKpx+fxEnY8RtkCiHyS02X+ff/+mDfkRXCbiEB/3Xq/jooXvxgx9P+B+HV1laV3THjp7SRFlOT4StyHLbnojPH0q54Hm/xquu+xHQ6+CGjUrSJifoG0nrKDVuw2Z3DyPTY1Xt5YaNCW99/4fZ2n8hGfs53tvPZrYP6XSIYlD5mG4GsYtQ/Q5RuQSSNuBzQ8ueKn7B2mor86rqWfwiya1BQNkq1REKrcAZLBk38imIJnSiGD1WpCbxDaUWH+y6nM7mpQhXss4lfN3jf4zM7KOQDsZBlxMs6s/znje/DNSNYIaARkSjxGH88tjtslcTKadeikZLhGUPcAX3ffKPkyf7GOZCFz/vejTxZUisAhWj4h7YsiGNC+j6Eb6RdFlNl9nswnp0lA00BdK+wK0coQQQpyFZYGKW+P7X/wWfSlJUCoUDOynoxBG63NSrm8P+tRHaWQRLx0HHZj6lc7wBkcHkG+zPjvMP730dEev45VhiEOXD4VZmG2gSIpaIOXBrwcFhxJ5ck5ByQfcCNMLdxXAfHXO4v8hfnTjMbSmMTIojQgpLpGMKBVYKiAx68SKc2kM2OQJxSrTvUhI5yvDovyBq3a+n1NK61xykS53isuMZeuMwvUMd3vv8H+WVD/4uvnpNsWd9k64ClMY5h44Me4/FvOahr+AN3Qv4l8XLOJ5czom87zfBUY6MK3jY0y7nQ295JmP3ab+Ge6SRzO2kX5/jRCAx/u+cU/+99T6QS0D65Vs+FjuOZkzEP3av5HPW8Kj/WOAbPzZkeV24OE1JbB9shNN+N6s0TRDnkMJxdGnMPw0NawDlmiSt8+1VB0rrcm1IV857iDiaLLCp9jNRy16oFtBS5aTABbcd5qrPQmIgktTPmnD+UkZrhIy3r/vNOZRRiPODdYb/n7s3j7Yvuer7Pruqzjl3eNNv7tbcSEKIwViMYrCRLOwwmBhYMmCS4CRrJWuRmGCMw8oi8SKOwDFxcLBDFsEBYxRAIINAphEgNCABQmp1o2FJMgJJtNTjb3zv3neHM1TVzh9V5977fr/mD2h1d473Wr/fe+++++65p27Vrl3f/d3fvYFBBjO3egwmRAfRYimwtqBVRQJgbNrbSkflRkylI6gQ8FixeM1KYzaiBJxRCrfHyl/hVa/8YR7bexYnZkRlDdY/xrv+3WtAHweWGWAcliWw2iSgbHPyDMA+6POBPbRvw6UFaJoPx8AKx3/zgecwfu8JD7zlnamjlQYKY1EpecUrXsHvv/MddNUpX/R1L+ads4JTSpaYs4faAZkQUU3zy1AxjhV7ccRedYi1UHZZhsE4JhEuN8KFc8/m1+bHPK6WfACAwqUW5rYkWAfuMgu/ojxf0c4eIFWZQM92H84KTLbFQiMhAEV6wNBwLkTubnyK2UOzaYigi2tgk0bbK776Z/nEXQe852d/CJgDNglqxwiyBk5RlhjmqK4RQ9IBwu0AigOaYxuAz+aPOtezicvUuRRrO8BLgGINk5YXfsdXIddG3P+Od/HsdaS8PsdVJSEENMTUYI6SkRvhTpdg4Ye/8Xv4zl/9IW7oU9vKHYYE/ACcQaRBjAWjtOtHqc7dQ90ajJtSlYL3LfW6IbqCTiMX1jCeeWS/YKGRtmlALNY4nMud/qqCU38O7B5JQ4gz1xuabQOplsqe8sC73pTUA9UDC+hOocypEat84IF387lf/Fe59OCClzzecmlVMvJCkDbRbiWyLoWpD9xc3uLowhh8BWG30nVAixrYMA2ARIOseKxzzBawKByn4ymNK/HGQYBm3VAWlmAzvZFUMgeGg5XyuY8nIgfAAcpvNWz37Ux93KXwDnBabd+/AKrJuUdY0bCqGtqioG1BCAQTaZ0QJQk5nzDhG77q+3jW+Plcjc8hyLkE/ABBb6GtAldAbkA4zYHPMMcp2ROJlkZSQ/sSGGPYZ9wUHJiCYHIFj5BaZcYIanFS0mkDbYdTZWQm3JILMLuQXgcAACAASURBVBE+ulizWNdc5eN4elG4oa3D26jtaqHap7YV2rWMyySgKqWjaTxlmQK0MkaOFFxMgZ3ELjPSNPOMI7iILxY8yscItLhCCK1i+p7uMLwJJhHRiCMwUkPVlVyaXsE1Fc4XqPeUIhzFAHXNl56/wrtuXWOG4diUUDh8u4bCpOBv5FBrECmhOoeulRAKovVMLr+Q1bUPgTQDBBSTZVcFIiiBT558lBdf/nxsY7hSjbnY1ewt11ifMuXqQIxB2xaLcBRGfM7oLj4+g/nFEZ04isIQOyWaEU28DN3dYE7AHqN+jQwybtj6jvTWXeosFS/wpX/zv2O8fw+1KiGCCcJILOXa835fcK4o+PpHhMu3lCtLy3MrS+kLiI6Y/ZorhbR5Wh66VHCAY8YZBbQBDdlOp5dNh7dMRczUxOSTUt2fElF1qbMXcHdTcvRROFos2I+BUioMBkKgGx1TH5xyoJEGh1eD3NbvZUjWA1VohBYuLQJ+7fHW4Z0jVpYlQrVsKMTQaSrpssYSYouhRDS1vTcF6fAkllr3ce4y63iBWJ5j3qz5o/ffx/jCS1nfnJMYZcMDfs4GDTkOkAh2ny/56v+a6txLaUk1y7YrMCK0fs2eG2NPA+c+EfgCW/H1L/oaqk5xAtFrSqp8wvDXX/T13CxucmN+nbspaFBWMNjKZ+h9fLqBalIx9hXWRyQqISiFscQQcaqMI5zWaw6C56YKnTg2TWqMS+MdFNwI2MdQQyjBFmxosxs17OHYxqfnRJvRJO7scPiQKdWNT9nr2BG8x1YlXj1NUJbyXGbdJb7wW1+D0xlGCrx6xEacztgzV3nzz//vKEusEXzs6+qf2ft+UraRAQE24GjcnE0QgzcW3BRGF/jmn/pFrk7HfPBSwRd/1RfwwPIYworLdUtVd5gglNWYjsC8awmHIx4drflXv/q6HL+z1e56imxYwM8ZfRGSADMLPviWn+aLvukKos+jrqfUPjAaTUCg8Z7SKM95cEa3OKH5vHtozo8IIWKMSaXZHkZjqLuWG27E33ntL/C6b/uKBLAPMnhLtbp9WZEy5/3veQOYZ0M3Tgru3QJMwEpBRFDfgRGiNhyu4GitFF2Ls5aoHZVNQr6uiVyo4HnGcXzsoTUUFNmNxAFuHHHnO8OCik/6QxZmn85MCGIQaxO9oNdikY7VylNMK3wdQBwSI89ZGl75dnjeao1BmR2t+KlomO/WZJMFRjcsgyGV4wByVqjNOfDqqWNkhWNWdpxUQvQJEAqF4Rd//02ERG7n/vHnMXn5N9O6u+j8IVYMNnhicKidIO4KcATRJUZCDKR2FU89/fGpsD7D0tfOh/y5h819OPZ8weWbgeoIbu4rtU1AqrGSsqFesEGJklgeF2qDm5fcf3JEacasJGLKG5w2BtMTtgfqtxRSxtwEwOO6FYfGI+sVLQZvHaOqoG48e2PH5KTmaHbMKNRoaAkI1lqi9xgx4CMygX/9Wz/DkhpQfKeIeKJuz2pDGypREDqgxYrhQnWZYjlmVE3xPiLGUscW60DWC16swuHBZd48v8qsOiA4gWmBqwymiATjCWENgJER5eQKzeIqdSeM3ASYgrT0zMUhmmDQmLpwLVmwsHNcM2bkK177tp/jH33JN1F1HvEC3uaqzIjxjrJe8cLTq7ykm/B4fULYu4tu7ZPOW4Sm2+fl3/LPePe//QHo7k/Zz0GOU0RocvmIAZkAV/iyV/9DWv08ZuHZrDqPcSOMs5wGz3jPcnW9YmIs3/x45NICxmoxWkDsW+CmFtNE2yMARLPbbHpYB6jedsttrMnlWcGnR3KnAtXEKjaA7zt7SeToJPAZFl66mnBwuibGSFVWaIDTynD1fORuDDcwzPRs1dKwALJkasDFjn06XvLQmmlbElGWk5LVNLCeGg5roYqWaB1BIj5EKlOm1tMoIgpaYIJF3YRVMUFN4A/f93a6ADiHhBmjYo8143TRIeqLbD5cvwFFrUkkchndw6l/ESt1YGwSci4soepYR2V0OGF6Y8HhMjIJI0axQFDUR6ypiAK2texVhzyyeBSIWSUppvIwhsW8O6OHZAIhdtRlQ1u2lI1Q2opAoAkdilLaguAbrEQ+/8IVHjpt6awF7VJwa22i3SlIFIydYHwJ7EFYAw0pJvW31dsNwQyBAgArgejbHNNHDI6uVdRYQl1TGsEYgw8tnSg4oSgsPoyJ7kU0vqYTJRgFVYp4jVIKMBfReB1Ph9gMxjlNHQ+GFJfu4g0b8Nhs9X6IadKZMYwOYHSR/+hn7uXh6iKn3rDat9wXHPzNL+fm29/NV3/iKp9Re5yxrLo1TAtWB2P+eFLwA7/+k/wpVzkh8HSoCw8L+IEzkyZ1MPQQT6C7gXCRsamwboX6EyrjCCEgfs2FkwCTA2oqbnVgEQoLTRMoCsutazdx2lHFhsePH4ao+aA5wO4JOywWlQi6ZvXgfRTP/goY3U3wadJqUEJoMOWI1FHD8pE/fDflPc9l4g0SPC2BxjQYa4lRiRKxWlCsV5RXjzkkUO+KUQ1pYW8sgYAxJhbGjBFxfIlgAfVo9Am1DqkjR1svGY2OiCKY6DDWEsSw1yiftYS/dCNRsh+6WzkA5rtMtd4GOU7ZJO2NwbMRMnW2YBU6furf/TyfzyXOYRCEFZ5GStbqicawLEqKYkqtY0wxIfoGI4KxEGLJaTPmld/2Xbz9F95HjAlO1HzNjQ1o3PoOoTYHVOkQ1Jf3Je2fg2XHPR9fMjqccHxoaKcJ8f/UGEZW+NMVTNYdVj2uVbhV8/AnZ/jqLlpvMSOw9hRt7KaznpVdcGkYtu0K2I9Nxxv+359mYc8nFqa1vOI7/gtWTWTsHP60Y+JPef3/9SO84q7PpCkhRqVyqQK9TOqerHzLylmOvWeNprmbk3bDZBr0FokE9vYmlHXFSMb4pkNM0nJzrqDxLXuuINSnhKblr5y7zCP1TdYKdnRENIqPHUIO3lyFV/AIxfSIbjEDOyHpIOTSg4FquZm8JqIoK13z7x/7CC+9fB7nHWsij7PknnIKnSIxIFFooic4wZsVI/8wL770In6vW4AGxmNH23iiCs6OafUSX/nNf4/f++XvBO1FUocUNyTrD1EKqYzEHNKEIxbtPtXeZVQiXUzlql3w1EYpDy5w2tQUccY01Dix+c5TkwQRyY0mssnW/w1xjJKl951g+lQ6YYTU1i1YjDHgNYtbK5pBoOT/A4dYztfwrGO4vDREKVATUQ+rw5LYlOxhOEaJGgYrk7ExTQeOPSIXl4EL84ANnsUE6knkhmnQuGZujlhVJQBVjEx9g2hDa2EtBrUV1lTccAd87NaC2f3vQapRKocLa6y0tGGnzH7gA9efP0MATMXajwnVBaKZgiRR8KZrMVXqbrbwgm2XnLMjpDYUUiWWirXEtcdVib0uwbJXTREs9g507ImkpQdgqngCb33kd/jGC19H1Qi2NXgBEUch0IUUtI4xHHYR03VJ9N9KZvq0ud4SNEZsNaFtHHuHV1jMZllyIGxlQAY3t/rkY6TEMFXHPoJtA85VNN7jygqrAe9bIkprCk7tiLWHajRltegoi73UJEnAa0CMx4dHEpPCaBq/TYOqDPoMcErdaX03L8CNoTzg7/yrX+Cx0SWuVpdY2SnlGNZRuXFuj/stfPGXvYwP3nwndtVyMVg623E88vzLt7+W99LyMU5Y0NGivTrLU2rDAn60d4JJjSUm5AewOFMhrRBZEMODTEYNLkas9ZRuzsi9mLXfx7ct4gsWi1malUYpCkuljlHbcDEsePP3f29iYohjo1qlMKRZu+nvIyRkOq6YlB3LUBPjBIdDLHg8MXYYUxBjDcQEdGAQ51j6Bd1EqXWBLQxSCr9536/xwpd/FhcRjogcY2jyFbftqwdiOV0QN5RNg4ol+CSq6EYFQS2KgcIQo8eWlkBgvVIKSowKXqD2HeMKnLFAh5HUXeEsyJOBxGB2Hh7OvCJrFcR8W0YcQSNN6PBY1iNhFSOujQQEoaBTpbAVIXQYBI0RY6BtA2JS/VvhIGUjztHIAdgK6yy+0UzhjdwRm/z/3XbEJcPtyILEXHLZcfcy8vKPeO7pWrxRYhHxErj/Sw5Y7sPJYw3lbMZk4RFx3LIlNwKsosm11x5nBQi588vwQJ+zbM6kScB6Tbk+wZWCL1qoW37nJ/5X8CaV4saOj6/WfMXyUebFPeAMUT0udFTikFXNufGErnB8wq85ZQ/kZOeihq3ixvAsZWc9UVqcFUQ9ViJKhxFN5YGYxGiVkmg8F/0NKrmBP3cJLHRBMDiMMYTOE4KgRojGErxQ7V+kOz1hq1U2XNp2IG7OgV4cLkb2vUfqU45p+df3/Qr/4LO/hcuxwEiE6KhcyaNlzclozS/8wa/zIfsC7N/4AUzj6ZxiJYBp8GHNSMLZTLnAJkgc4pgpqbQhQGUqWnGYkEAxJyAoRlI3pXblkaIiSks0a4IKnfHgHAbBIliRnfR8JNEZ08kgsmW0DMmUHfnu/t58B3SoRkR98vNK6l4JoGmNaWywBqx6RBXrFB8CagzR2JR5R+n6xNrmQGB25tNwfFcStS4SDiMpBpgEoWwiGgMHUbk1OuAdszXz4gATLNO45rMPhLGsqY3lNFgen7esGLNuRpyUYG1B6DzlqMKL4n1DUUb6uTW4mBR29kKTSCj9HJBUmSCihNjQeSitAWMJ3lAUjk5jKoULHYUZ4YMSUEoNmNKS/sjhmzrp3hDosiz0cGbTn2Fi8GpYsmZRrThqJtAKhiqJymuD4DCupMAybloKC9Cl7mcmgF9CUWAne4jZI+iSQImUBzAr0KeFk/FUWcTSJGBfwKnhAso//Zrv5WBeor7DBsUitKHBFQaL48RNeHTv+dTFPvVqTVU4uhDookUtIBZjPJU7BeYJ/MmLToxBw1DHy2zOPGknN9uqlqKC0Xm+/adez0PlXZxOL1FrOiNGHNIp4iquFi0fvXDE3a/6Kzzwzvv4S9dPibHlR979Rt7DYzzEjDWR3NKEHRX/p8yGBfzkcol0FHRpMpkIcQ7tw1RiMQbue9O/JAlPQaLlzfjKv/3DqDlkPb/O2k3AeyprqKJiTtacM1PGq4YL8RRWp6m0B7Yb7banyUBMt4cpSWOk/iYhTDFuj1j7dJiugBjREBC1qDWEUcupa5EQiFPlDX94b37FSEuDxfDAB9/DCw5fSAUEWnpHeCZbOBTrx0kjaN/9JWmEFMbi6wYmAu2SqljhVUEbptUhzbpGo2JLx2Ss1AuPhg5xCSza9FLYBX/UDJxp0AfphqgxA7HCKcrcwCJ6CgxCgQEaGmzwm1gm5m5NZW5wJeoxBEL0uEKofQfR03UtxjhiHOqmwdnPXYBdIDDXiI+6wD1r4XOOFasRY4RohVlxzMm5Jc96eME4BPaWkbUE2olSAuuQ2uGinpApLJu5NMRJtZkgQNeB8Rw1AdPW1CNY2A46hVAkSpSFKiwI3YxfvO+NlEg6jKLssc+rX/4f88n5LU6mY1YAGLAlaJt/0p2LDssS6GNoCLz94Xdw6cI58IEqlIluTaTrOsZ2jzq0zHXJ2iwIZc3JzQ8zvfzFLNeAO0RFELGpjAIQo2jocM5hgIP9Mce3Yj54Dm0fPFsKkA7eCeiPBD5x60N83vgz8GXBtRaOJ8JeVaBdR4wNvnC87v33ckzNghqqGmcjBZ7oVxRFR2XX3P+2e4GIyIOkvshZ0JL+osPxYf2hAHL2G4NvczvxfrkYQUPa3WKXAPzC9SzjpDOmkvwY0aTYIgRMyaa+0uz4RdUcVA9onIA73Efsy9rEYzihsMfITv17xKJZ7+5i3XJ+BIVqYrdqQDVirMN7j9dI6GMIR5Ye6EvnGKCP3ya7Yp+XVCg7RXygiMoCw8wccq2cgndUYU1zeotCAw2KtyOWMiaWR3hjaHWNaTqKyYimXibW4igxf9iJSwc3XLe92YDBOeiiUFUVwVqMF0rn0OgpioK2idRdpCiEsizROg2ycem81IWOEhKzRcHZVJposdwJwQ5nHZ4tfbR0eJasecujb+HV+9+QujarpfEtsRLUeFbrBX5U4KcWXSkUYxhVVKMRIZRZCFrRGBFbYKfnWa2vAgWRbYn40MKHjfuGLA0ulFjK0Yiby5o4FUw0WAWHTQntpmY2OuCxao/OVUlr0RqMWApNL+YBCTVv/fkfA24lUF8EomwlkUQ2GkyDMN1quNnN+TbudDc1EAqiL2jGe6zNiKBCNXZgoLCGZeOxkwmPR+H9BzUf/Mh7+e4XPJ83v+11vIUHuUpH23e11KcPjhkO8CMm0e+EtGtEcLbEhzXwCO9+0w8C4/zkJcnpW9L0XvPaf/s/87f/s39MpZ9NV3dYO8Z5y9Eycrmx3N1Eph04PLSpzCDVpQ8xF5WF4PqMoyq4OfOHHqB8/nNpuxaxBo0xHbDEYXBYSa0Pf/mdr+N5fkVBhQI1LR0Rk6f9yFqW60UqKcCmYE2SUNjA/GCy3pMLW7TVlggBHx1Uk/QkOeW+3/iplAW1+3zhq74dbEAl1UYTA5UbI8bhxdGI48yICKlcAoi5ZnRAbnBjKlmeuG/ZCHip6LTg4XXgpaMSn0NWT0eBIdJhsKm7ixGIIQnx0kBcMioi0bYIBZPSp/lbWmI3xDrqbLsptN1uGRuAQwCLSoG1guJTG2SbBGhfdt1ysoy8b2ZoS4sYoSNixVEgWO1ANblFJ0mYT2Dr1iNDCuDOUGglsTkvdgXTFaynjgfLDl8mhhhRwQpt2xCInNJgMJQUKJZjOn703b9EgefaH3UcczV1WvLJSaUscNKM8EObV7mUt8tQ/A1O+IWbb+BvPecbOH/rIvvtCNHEcHEEqCLzYsHiaM6vPXwvcISNV9kb7dOEiMfS+VTOaixAxIhHwoLSrhCdAwuIzTN610/GLKmVdlCIuKw4Fjhlxnyv4/r1JS/gkB+7/1f4u1/6dYwmlnt//014hBkNXeovlDLwocMUSw7cknf/5uugakG61B0l3iCQtJLOtgQdjunt2gZGcYUQQ8QWgrgy6UghFIWkNuUYQk0qsAwVxjgcFhsK0HRY2jTCyQwoUZPLpNiAP4OyPr7aUJ1zAOSA9ibv+t3XE/1l0H02JW269c0//vn/Iy84VkzdEazgRBAB0bDhIhrMWfZ2z3zNJWPD2hNTibPkfSkKBDFYcSjJX9miQNc+HRKt0FJyXQ4p3ZgmeNSW+KBE6rSYC4upKjo8prRoFCQskG4BrBmksHO2vsulgVQuiYUoiFrolEKhHBmaLsWe48Kl+WCg8ZIkHNaCjylGLUqLdgHJ4GFhLERFsUTczjEnDitsgG179agYo9SxYcGKdrJi1RhK7/EWFtWa2rW4fcOxOebex99OvOtrKYoSr5GmbbG5sY/4iFhLVIt1U4IZkRa35QwzY0BrsA9JDanDoEe5huefv+11PHtuuEABeP6TL3s1Y5/OdHHsuFYGZlNoJFJNRzRrxaVKVgiJrTgdkxjVcgLabZObxiTXNzgHHzegT780NvqmAL4Ff0rz3j/k/Cufwzx4ytEYn8ms0QTs2BE6OBXH1aNDvvL7vpPXfN/f5ZSPcIuYBNp7eYbsq54Otv5wgJ/e+pSdQAgtBYaOGchsQ4WV2B9I08clRMYsOKoXPP9mzUG3h7Rw5ElCqY/c5Fm+xOmM0/Ime0TW7CLgA/OCvSlbhXpdgiwQfxMYoTpO5RJYDEI4XRG0ASmZ7Sk3Tlv2QsACTaYzp3x6wEsS/bJSYnGJvaLbSw7O+jdtSWNFhNAlgIKYaIvdGgqXDo/dKbiOB377Z2EJVSwYBUcVIvtf9t0EHwhaYNSx2U03xJ8dwGdwaaitJYpwb5n+aAtWEeZSUYglmoImBKRw+KzvcOJKChcpRw2FHBN1zYff847cYS61fjHlY8lzdrezC3Id05BskxWKbLoAbDLdHegCo8eItomaXY6wTuiicHkeGQfDEYbTWNJojaogahLxWyLGKrFbIzYLDvY2tLmlJoOiBvBIFEoc5uETLuh5VrMlesGxLiWxso2hWXouNw5r95lZIYSIyywz2eiHKCcjQ7tqUa+IsWhMzAIjbECfIQ0VsEk5BpJeTcTzKw//Gt985dXI0rHXlWDg2Mw5Kee8+fS3OF7c5IQZ0DD/1Hs5eM4Uo5HSnqdRh1hD9CucaxkVNdQ3mH3qfcA1YJ3ma7rs4GzXV22DOE+L4YHrH+aA5zOr9rjazHjte36TkgA5MFvLlLUadDzh2EzZcx0f+p1fgngMoyXWrChMQ4g1pbvJUup8haGmhM0WYDCpZaOIYJwQYqSNiisrxEPnA84Zuq6lNCWqgpdANGtau8rTtEStTWL1tsP5iATJp7Xdbin52wHOr027TgW6BqxHwgzUgq7Y+ubcFljhYhPYP/WYokIJdF2HNQaDEGMfJ2jy9T2lYWDssduth7NUhdAfBlUxxqCS4FiDQ4NCDGhRUNeRWhwYn16hIOuIpKRmCAnYAE2M0CKyvvEpUkevMMjptGsREFVaH8BWiAgOBeOIbUpeCIlFvtH4sxaJ4Ixg1BKy8LiY/AQDXiPGJVDW9X29+7k1tPhhx0L0BFEWuuTeq7/N11x+JUW3JpSW37j6Nlo6DIE1LTNWtI9/CHv3F+JGIzqvRGOwSJLAkJSkDNExGl1gyZS+mkQ2ZT/DW48J/EmFqjWO++af5C/vfw7XuxJXC//sD97CPisqkt7fDc7xKfNh5NWfhcQG6wog6eSmThNKDOt0zqRLHS0lh+v5PP5Ud6p6KqwHX3v3G2GzrVsCUzp+5Uf/KV9++dlcedmXc7M1aFVRldDWgomeSRs4oKUIM/63H/l+mP8xFZ42XWDnWsnszvWeKhsO8JPacexYxEKmBucDQ0zsAM0Z3YTbJmdWIdy9crz06gHzD625sjZM1jARRxVGFE1LPY48fCRcxHENS20tMYb+coMyweZNNWmJpOqlNc0jH2Dy3D1WawNxCjGme7S57sbDfSfX+KvnL1OdtrguYMUhxlAYi/rUUrMoRjzwjvdS4TbCcP0QDWpt687XXEgvKEhH4QzWQEebxN8iSPC5LWRNMLf4TL/HXR5+6Gu/i+ctxlw5TUNpC0uhiuDoa0T78q4NaizD1H/ou2CrgojdZLZNTEKnzfQi18s95jLi4dmak06ItkAomC0D4f7fpSney2Z3ICKlQvSodcT21qYcp0+kJhvcIjzbikXJGd8MLuoC+BS/8c5/zvd9xcsZV0eZmmAoXAXeM3YlFSWNpBr0kYBTx4gRNwlEE7GV4CQQ+pI462/nPw/CZAOOFhQ4Dim41BSc96nbxPMWnjq2TIox3reEoDhbEuTZXC/nqeNEhDKuuKAnaOMJ5SHzuE5wq/gsrpr2i551N7CjORuKYmZ7RY10xnMrnvCGq7/K11/5Wp5zchmxwrULN3njI/eyYE7Nmg4PLADD/JHf5eier2RRW4y9QAyRwgVKbmKax5g//N783JbEgN2ZTAOaVwr4TRII+vUXgFZq0CnlZMqnVi1TN+V8AbJeYulwdsqsuMRsdI6PnXbcKqasf+9XwZVAA6ZGWKP+mLFbMH/sAyCJ8WMlErWPUQZiPb0dk0pOQ0oOIY7gA+o8hS2IMTGACyMIkao/QFYOGUeacsXqUKBbImZEMCWtdowcFA2c684hYlODclekji9Ds13WjZLatqumhGMIlCidMaiazT6pahGxFCqM7IiyylGBuMQkzqeKauTygT6Vrj7hFBrQGtyawVJSSIW1DucNJnqsWqzNDRBMCabAWEMMATudELVBg2wCAjEVqh4phY3UJwYqh7epwFxoUJsHaWB7IXBGPFjRNEdCIGrq5mi0QLBYMRtOgkiSwDNECqNY01dHGHzwqDWIMXjvic7gY1JidBgk2gSgDW9DzFtTzACgATXURB7lmNde+1Usid3SZNZZisJihgXXjFzHsq6hPEIVPBFrLEhIROpo0Hie0bmXUJ/cSPpd9F2Th2VK6hDXh4s1LS1HvG9ZYDkiiDDRhs8c7TPVDo3CgjHrfcvIXKdUJcgBXktilmIorcPEnUT37f5KhjdOvcXd977D2AzAKosIvOuf/H3+059+A3r4Ak60QjsoouEwRO5q57z+h/4n9m89Bh+7D9yKpueT7OSG+m/vKE1/Cmw4wA9bgbPdPNpmYHZpr/mDirrN7tV4RsZz7uPXued0n4O2Zb8sCEEJ0lDbJadmRixOM1Vb06bjTO6CNTDLp2WJPhF/lNwo7jrN/E/Bj8Ac5sEMCTRDsdZy7A64MZoynddMbJ6EObOCgLOO1iRdke/+W9/Nf//G78WaLGA7sPpgSJ040nClevrC1aiu8D7SLQXKIpeXGNQ4NHSMrMFJwz/69v+c552Oee7JjPFySbAj6onBGEdT1ZvDJexgTGeo9AO0ndK41PuuF/aOrJjwwesrhD3WheW0uMDKVEg5JgTddEvApM44KQOqiJoEVHZrCtPQabcRKn46HOFTZnrb1/57ASRimVPqnNKlemgMKWNcFiAJ8BBSeVMMiikLrEQCp9iyAqkh1jSnf0LSMyON8cB8lhCxSApwc/ZSaXFFIK5OOAgTZGUpcMSTJYWpcLbi2CjvrWesqNB1ByiOwGftnaecBlam4qOzazurMLeV3mU2DNF6NDSmEWs1EKThph5z79Xf4Fvu/kZC6PjlR97IjAUtyxTMukRhV5ag1zj5xO9z8cVfx2zdpVKAeMLywXeDmwFXMTQghqhheOm6jRl62F0zkwdIc8AC0XO8uokt7uahrmFc7HNgA5XdY6WOD9XCaSfcsOdojaGwJ1haisrQNKdYXdPc+DgN10EWlJWlbeJOw4AhWcQ5h/eRGJJvRwKxuU5p9/LhXEBN6mDVB60GNDoeGc0oL834ud95LQUOS8WKgDLKoXLNGMfff9Xf49b0mJomBw4xnVqHNmQbsJq0j2WoBgxd0xK0TRUhCtgqBRs+4LvAaXXCfFwSJZJkO//sqAAAFkRJREFUBRJab4B5dcrKLWhzLFqUhq4d2uDcaQahoWZVrLCVoNYzDha8oNEidpqfKJstM3Q909CAibkhRD/xOqwRjHYYZ2hZY/3jRNYYfCqbGHKsBRtZJwCcx8aHqdx5iGMUR5R+rNJpx0dhdm7FJ3WF9Q5RhxYWH0OWy4gYOubFjJODWyxZ0NKgfXOIgbr5LYs+gT8BZSnrLXtpR7Gjjbt5jFuYeMxkfDerFjJVitA2WKuodhjj0SAoDjRinKSfBzpYoa8YzbINHsuikqQrZoW5Rtr2GoVfUzLBm4aTY8/8LT8DOuVLv+ZbaeOYqCNMUdG2LdYeA92Z62yW3oCZ1Xe+Z8kJkojHAytYX+dn/8tv4Tv+zVu43o2YjUtkseRSXPP6H/w+zq+vMfvY/VTMaaLfskP7pMEd13hqz9GDAn62ZjZjFmFbStFbvycohFx0fZ0Fr/m1f8xrv+onOaBgfu6Ux82KcVkxczO+543/gAU1M2paPJ2kGsXYDRPV7bUydt+3pSNwnTD/OG7/xUQVYldjxiVRCmhbolOumwkPPHqT5xxMaE5PEAzGGLyCc4Y2eHyptNYjE4MnptitjwQ3lORhWOyDAwXoUH8djQ3GTKDYT/qWNpEeaWuMV6oYONDIm3/x/2avgT3GWIQxE77lVd+GdRXXDm7SsN4MyZn60M0GNVBTyKdzRGPWzHDUWG6O76KLV+gE1JbEoIjXpCc1niLqkNgiBJTc5lYMikEwlK5KPSZkC/o4KfAaiMThTK1+HWy8etx+5vmxoOCxtI0CJYTUcSOlnSyxMHR4ulgn5kJoMS5SMMOyhPlDBKmBWUqle5A2gSgBHcxYKeAlpCxb8LREOgJvffRtvOLZX4y2LbYesS9TbAOFQNt5VlXJDfaYlRUak0j4yF3i95YdURukauhG52jrB+mTv2GnrnrjI4cyUNl6OnA0mYEXU3vW1nquhRv89GM/A0ROCQQCDocVTwiJ2J9eYQ1c48afvInD578EjDL71EdA5hBWCIvEx9vMYZcP5zvgyWCsP6HHnmS4NYnAAu8aZt2Y68UFolOiOP5o3nBjdI5lTFpcRREo3Bwjx5h2TX39IRpZA0uwHcSGNuOv2pd2DozVGXybsHkxBG2I+jj79kEeeM9v0nWA3fox0SzorIkR+z/cOmFEg6C0dFhKuuyHrCjWdDThFr/y1l/HUzPnBGLIGejh+Ks/y3SDJgoxkHQUTQlqUwCgNsVJheX/fNuPclfwxAxH+gz6FBga1lyf3KRmRaRLoM8OWXSInaoStyLdz288ci/7HPAVL/hKRuuK/XbKZF3ltdiXhkjqGBRarNsjhL5bms8Or8VYj1NPWXrq+lH0xofo9BawQuwmAzy8wWJbGrPBFqQD/xgffuDf0Pm9VBInJoERfQCb/+B7bs65hCXSZoGGImkoYYCaJY8DS9acsmbNOgvSb641sPE601pd2Uoq7N5PZMPYSO1IUiwZ5Sanj3yAyXPvgXYM0xJCnaj70mDNAsKSshDKEq7PIIZ0oSGWL6Wko2CiEDUmVpzOaJo/gegAT0fgGi0FFePRRcQKAUOlHyO4gve86TXI+CK6qsBOoBQInwKWmaE27I6pvSlnic7g89LI7KacwIU1LE6ofuutvOxLv473XbnIFV/z8z/4D+GPfodbzXVS5Nlt5+JmzibNwV1iy1N9zhkU8BNh221CTaIJZ62LzcH9dseVP7UFp+zphOPpdWK14nvf/P00pHbKDR2PcYOFW4OaVPo0WIrBbbYBNJKQopGGqMdYneF9apsd6zp1B7IWbWvaYsLNds7cNlRuhXOW4AIrCUQbsQKdbXn79d/n9a97Q0I9szMhDnDA+gVoBGJLvXwIGIM5xHKEtUfprCMtpVPGTnju0QX2Vi1hdczaKStrMWow0fF//O6/YN12PMAHEvCzw0Q7Mz8HOVQmi3wnymxfWklPtcVQuxGtTjOXVEA9iia5KZ1jVLCxQXoxYwxRHKKBUiIu3gJaNKZadQ1k0GeIZjZjA09UvxtZ03D1wk1KqShWgZFLouqT+gixCa5tRh21eOZxxXJkuMYfc7pcgJwCNcaFFIxo33hbh9WHMGPGQRNUb63SxRpB+b1HfpcJY0bs87JzL2N/v2Lerohjx2I0ZemXLFwSqiwsLLuAlAeoBChPiPMlPYuo32+32UEGuQ5jvxoiIJKEFqPiqcFCG9cY29O5TSKA9fQ5IbPtQmJ7IsweupEOFuLBJACjtw1DMcYzc3k4tj1MAjuMu/5hBZacrB9D3Yv400XNYzGC2edRc0hrBVt5TFwTupt0s08AJ2m8WCPaobtMsl1/D4ObX5q38QTot8CC337jT4CUedxaIORzpgAlqdQeHk2vwHYgcimTJR2mYpsAMm0ghp6AADE1GwpDO6PvJBlT15ptba+1gehXWHEEnydc0aXB7Vac7C2RpiGYpM0Sc6KjDIbGNdwcz5itlkm42GS8dUutHp6Z9PnW2uFR1nS86cE3ccghFsvfuPwqjmMkuBpoiDEDGqYktHWeSg00pxRjwVUNbXeT1bWHWbEGs0D0GoYalUx6zbHv8HzWFlDo8WMRiHFFd/xBaG0uNLr9CQn4eZwJVxGUVV6KvdCAAdY4VxPjAuti6u8i2wPuIIGM3p6QPbF9zm1Pzd+cArdweoOitPhYgGkxYY3TBYVdsnj8Y7RdA5yS9O5y7Du0seotiXImhqKGpJ8Vb5Gyrb2+mKE1gba7BvUtYAxLzZPFoccVk8svYd0pRg3OnmwS3ajJ4xv/jEEfiN22H23Cp81PABFCxOqCX/qJ1/CtUnLplV/Nz7zmu9B//y7EHqNhlZm03Bkf5GRBH9NtCAJP4VjJ00lVE5End7EzbAkS3Up2gtmNoy/yEzVNYgFsgesc55hQYmhJwZrDUtOywOdORKlVXdCeXpo3H31yWU7VP1+Ljyc9Vj2v0eSa11gk7pM0dHoEvITi4IuIeokQRjmblEQcFeF8N+Ovn4dzzXXU1ZyaJW997A+oabP6eCQQaTJwpv2pqt9kn8S7f7rHqqc8JnOIFoDNt1AAo/yslJcDxQLnGPHycy8jNh3ihGgi3nk+dOMjeFIb85oFbQ+MqUFyVk8ya+3JIrt/3rGCJzdegsldusAbv12Lsb+nZ1FM/hpdeDaYIkUTVkAbjDbY8irlSFNHMFGiVYIKiMHSYcOC+WMfBnMNKSLaJmRJCkF9+6Sd4dM7t/oSE0Wyykg/XCH/IAHGVOxxxAXO8+Pf9C/YX08R4LMe+gy6KvBP/vBHeOzc45zYW9x3436WdKwJBHyuyfc502ew1kJIvuvJ4tZP61j1PhxA2awR0cgoSVkCFRaLAxyGjkhDxZpDzP5LCBHGLqLBgh6hqgQzxy/+GOFTWNaZeWeyXyRnuOAOcODPaU+7f+/ZcJrBWCN0GraAFuTzt4AkFpWxaRvbADkb0Gun+6AB+r3vzwo+nuY1CJ+muaUgWWNL+89/c/+AHrC397los4/xE7TcY1WOiPYqdNdh9TBwClqTNI8CaMSRShQDJrUO09tW3pMEF5+pdSiRDPInnR9F0oTTvtsp+UBZss0hmtxPInc2iw5nHD42WAlEbXHO4EMS9E3lZNsqjMH5rP5rv9aiABVwRDG5gpUDLGOS6orSaQTfcTgq+PJixNgHoqT91PTilMCqbHnHtffSWU+Ii8xSTCfNT5dszTMzrxKniRgpURwRg1BQYiloOeSUy8j+XUh1SOgmEM8hOkH9knEV8OE6mOt084+RNMh6kDoiNECzieckZ6aerM7W0+6zYCch6TLA7xPIowWYKiNbgTMdQ7GpbH53ZvSijPQxWiSNWcDYiIbdKqjcgY+hnXfy62z8kD+7Fz4RCJ/x6cSemwLP4uC5L6MLY4oqMP/T90CxSkmQ0BeLd2CX27//NCSOnsmxSgptXRqHOyrfE3MxyahY0Kr/w4x0F+lf1MwCbUDbvC/25fS3ddUb0l64eRHYBO+hny8ZY5DtOjFaYKjwTPmvfujH+H/+l/8W2luIRpIHyi/Uk1c2e2hBKhD2ae31ZWDwlI3VsIGf3cdgZ1LlCUq3BYZ60ULthz+e8QUBkL4DFnFHh6XIh6ohHQx6gUbygkzAD0QKGjoq4G5G5/8ybXc3MR5gXUnwa5ypidowaU4YdR9lygmBhhVrZqwJJgW71ghht5PFZqI++ezKMwL8wOZeCnUoYVMq028mStwcGB0FZXRM2UMyAybQ4Wlo8Xg0BWubsTD57+LOd4n892SCkmcC+LEZtAo2a0BsNkADnGN//+X4eCG1idakWRl8g4QVWn+UFHTsrr6Yd50WXAd+DqZJj/fAa+9gB7VxbNdhTz3eEAl3lqcAXmCkU+7iEvtMscDP/bWfRAvDj/zBj/Pb899mxYyamgZPAKwYgsbbrtW3y33yCYNnAsw486Nu99veR7OhEOf1iAMmwEVSoNLlr/tMpheInFIvH0W4jqFJh3PpaQakWqknCfrAM3SIUijVZD/CRphTckmIBnJGT7BWiDFsSS677zbPQSOGqBEx/dcewzCbJ/VlZU/GnjHgB5AM9GkPWvf3JxF0CtyFK59DUZ6nDYbgBE7/CDgGboGst3tf/gxsbksejRDV33n9IR0M+iAXUpDb/yCpKLc/B8BOsiT76O2bVDRnja1UxBhw4okKzoH3Od6SBJgZSJ2H8l4wKDCj/3omUHfACGSaDulniPWGVNzbcYE2NajKj9vsvwORFR1zGtR0CTLKW58xBhO3meFBjZWQfG9Mnc1S8Ui6l5yeJDAm+fNp/reP27sHY/aIoUbCnK5+COQmSCrp6jUCt7sFaO5AKMagnwaG1DMG/OhWnwyXERqfYvpNmWWfWCQ9/wzGsfN4+rHX0YvYwhC61PilcgWdD/ngGlE6hnPe2d3OcpJIdpKSu2KRmzd42/fiQPfYzrsW5DrIEmJad6qpaG4DkoQneK2/gD1TwM82No3bubLr3ze+Pyb2sE/C4LrTxn4zvXaTSX3TGtgBgNgGDoOJ3yEBNfFMZ54E/GSfvqstTMwuqICwD5xg83kxRrN9mpj8InkC6Ras3I3t0u/+4u/8Pxjg5451eyaTtw1ERPuD+m4Qtp3E2xfgjt+LBQ2xxzrxQkbc/aAmbM8owfaMn+T8XF7kQSrQ84wufAGhO8BQUJiGxcn7gTkWT0WDzfCFx9OQOgulwxIYE7eVXUoOXJ5+FsunbazEpA1jAy7sAGiiYLYd3tKmW1Bt7hmSkHMCKDYH1c2dmOwo44YHEjEZ+PmL2zMRkGzGy+UsZJeUDXQDlO6zBV/74poeGW8yPnFbjrdHwXslzEITt30jYqLb5w9kHd52htrZGLfPcdoHvJC6WY1yn7zIIft4IksaWlqUFUrcjGS/MRtsmkWSXknyhjIs4GcLXLHLxtBcuiap9bpungub44JY0JKzA9x3yGlAuhz4xZ3r5Of2HQ//4m88vdWn2WflLttpKomg2Dxu27GTuAs3p7tUPDaDzup2fF3eQ9OfZuRI+iNpSdTeow34EAU5yNoelGTj5yOamRrT6bNQcawWN0kgdWL4CDVKewZISvPTZSHnuO1QHg2ozaM+oOz5mXtzeTntxFFqkDNC2bApNcFjdbs2Nz5ql5FwJmHXs4PNFmB6mhMhn755deZbkv/Z6XKzMQuiWI0UO/GpyX6pjyMCgSiJtWA1+/t8gYIEzA6O8ZNeJLOitp+3WFDd7uvJ31jSGBYkRlkWFCR1tEpxRJ8cut139an5ePZDeRrjBvg0HTqxOfHoExizmwmJLsOtgW13Y0BiXodbUG1rLj33jrFJ80/yXzzdDKlPV5y1WSe7B+hotsmw3Sf2scDGP5l0aI89Szt1s5QNNHLWl22Bt+GMFdwG1vQPKBvofosJpPuzbIHmJ0rO9Xb7mTz93qHbD4JBJdh2Y1LiHfeeLO+Rt4M2WpFUNnce7299d4/t98GYEgLAZi95KmPSQWn89GbygXljevvvU719vzFuB3Hnb25DwjcvlaPpzXRRnjTo88zYzuEpOysR3RGKa0BuUN/8ILAH2FSfyTUcp0AKedN24tJ4m/51kpp9L+GSJuo2ozAs2wF34GxgeuYzD9vf90GGRJpcFpGcXjwrBLZZ3GbzOajuzsInf4h6Jmzj4JUdQCY/Rgd6C5M3yx783wAgGxqj2wQZu1ne5BOF6LP3E02Hdr09gB6onfE78czDgYCXTCMWZc48z5ukX9MHL2bnf0jHeSEHz+jG5w3Pcgi3EcAWEk1fM/DADkC4E8FJRPp1uDnQ58P87ia7a5r+dpjjlIZoy/i6bXO645ATcRSZSAybxRt4Aj/X/347P28PBAfpt87Ml/Td1lfHDddCWbNcfjI/ng6YshmLsB2unUAubFjE9BIb6fU/LeHbM2DKFsy5Y4Hs7pdPFMzfNjf6g9ITvg53xl9/7jf7zNsGbs75iZQE6eh1kNKTdkHnBIvVO2xgyV/7OKLPJIveOXReI4PbDftNKfaCuNvx6GPu/kY1tjkxtkZyr8eeXJFaaAtxi/SkL5L/XM+O8yB9FbB7D7usKD17oNkM6xN5mv6xsyPxBONx5vW2jOH/IGwDJiYLu2EEu2OW/Vj0m9+lMleDpOAqL3CzXZv07KkB2w4AoXFnVP6/du5oOVUYigLoof//wXemM/U+KDZAiNHSRs6s9dRKTc2ZgMkmWoY3jacXn04tHrzNIG6P/zSgfgfXa8s2LNvr2BSfsQkWy0KuJ+nFhpRy9vVbdTvVjp97O1FMviI21dl5uNFQ/VBXG52GbedbDbZlvz7iujNj/k6kr4j4F1NxJ+o6Pm+fC35QlKNqNuz7kCJiuXWvPFbr/3LxXn9xxc/rjCT+vlYRB42tWr8andrcZbg8mJgdfQLOzY26u/Lg+P1vyic0xs6yvXIZcNykbdx5uO1Dcwn9zPp6isdj7wXjtmvP6jsrpuL4fPNjisoXL+5d8xa/l4+9btg1q9V+xHV3yn1Pd8R3sDH7Wj+h0kZUbiqd6S5n1F//vXPryGE5hqqXrK73ipPWqtl4LMfIw2tPfVd6a1H/E+NrtepvRLXPu33dPbDf7qvG7fgpT5X1mNkZS7XFeOzk+4uDHfPZTsPnWc11T+ljc76VTfzF6njoebgzx6z9ybP/dBFmR8SIucMx52Drda/OwcWguT23VsC9XjSu+c9K81GvMxv/JnseatXvHRdR78zY6qdW/dSqn2vWc4ytfmrVT636uWY9x9jqp1b91Kpfq1an2zEKAAAAQB/BDwAAAEBSgh8AAACApAQ/AAAAAEkJfgAAAACSEvwAAAAAJCX4AQAAAEhK8AMAAACQlOAHAAAAICnBDwAAAEBSgh8AAACApAQ/AAAAAEkJfgAAAACSEvwAAAAAJDVdLpfRrwEAAACAX2DHDwAAAEBSgh8AAACApAQ/AAAAAEkJfgAAAACSEvwAAAAAJCX4AQAAAEhK8AMAAACQlOAHAAAAICnBDwAAAEBSgh8AAACApAQ/AAAAAEkJfgAAAACSEvwAAAAAJCX4AQAAAEhK8AMAAACQlOAHAAAAICnBDwAAAEBSgh8AAACApAQ/AAAAAEkJfgAAAACSEvwAAAAAJCX4AQAAAEhK8AMAAACQ1H/jxjTsTLuMZgAAAABJRU5ErkJggg==\n",
164 | "text/plain": [
165 | ""
166 | ]
167 | },
168 | "metadata": {
169 | "needs_background": "light"
170 | },
171 | "output_type": "display_data"
172 | }
173 | ],
174 | "source": [
175 | "import random\n",
176 | "\n",
177 | "# Pick a scene to visualise\n",
178 | "scene_id = 0\n",
179 | "\n",
180 | "# Load data\n",
181 | "x, v = next(iter(loader))\n",
182 | "x_, v_ = x.squeeze(0), v.squeeze(0)\n",
183 | "\n",
184 | "# Sample a set of views\n",
185 | "n_context = 7 + 1\n",
186 | "indices = random.sample([i for i in range(v_.size(1))], n_context)\n",
187 | "\n",
188 | "# Seperate into context and query sets\n",
189 | "x_c, v_c, x_q, v_q = deterministic_partition(x, v, indices)\n",
190 | "\n",
191 | "# Visualise context and query images\n",
192 | "f, axarr = plt.subplots(1, 15, figsize=(20, 7))\n",
193 | "for i, ax in enumerate(axarr.flat):\n",
194 | " # Move channel dimension to end\n",
195 | " ax.imshow(x_[scene_id][i].permute(1, 2, 0))\n",
196 | " \n",
197 | " if i == indices[-1]:\n",
198 | " ax.set_title(\"Query\", color=\"magenta\")\n",
199 | " elif i in indices[:-1]:\n",
200 | " ax.set_title(\"Context\", color=\"green\")\n",
201 | " else:\n",
202 | " ax.set_title(\"Unused\", color=\"grey\")\n",
203 | " \n",
204 | " ax.axis(\"off\")"
205 | ]
206 | },
207 | {
208 | "cell_type": "markdown",
209 | "metadata": {},
210 | "source": [
211 | "## Reconstruction\n",
212 | "\n",
213 | "Now we feed the whole set into the network and the network will perform the segregration of sets. The query image is then reconstructed in accordance to a given viewpoint and a representation vector that has been generated only by the context set."
214 | ]
215 | },
216 | {
217 | "cell_type": "code",
218 | "execution_count": 187,
219 | "metadata": {},
220 | "outputs": [
221 | {
222 | "data": {
223 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAr8AAAD0CAYAAACSGU5oAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzt3Xm4ZFdZ7/HfW8OZe57T6SGzJhAiGkJAryBRFPXqRS5iEIWLovdxvKByRZRBBvWKoKIiCiIik8pFhCjDoxGQABIIhEi4JqQ7naQ7nZ5On7FODev+UXVqvbuofapWd5/upPf38zz9PKuq3j3U6b2qVu317ndbCEEAAABAEZTO9Q4AAAAAZwuDXwAAABQGg18AAAAUBoNfAAAAFAaDXwAAABQGg18AAAAUBoPfAjOzl5jZn5/r/QDw8GFmd5jZk871fgAYDn02HYPfVWZmzzWz281s3swOmdkfm9m6c71fkhRCeE0I4SfO9X4AZ5uZ7TOzBTOb7fTLt5nZ1Lner15m9nIze8cqrv9tZvYq/1wI4aoQws2rtU0gxSOlr56qzvu7ISGePnsGMPhdRWb2Ikm/LemXJa2T9HhJeyV9xMyqq7C9ypleJ3Ae+/4QwpSkayR9k6RfPcf7k8za+BzH+W7V+6qZlc/0OvHwxYfmKjGztZJeIennQgj/FEKohxD2SXqmpIsl3diJy/yKM7Mnmdl97vEFZvZ3ZvaQmd1jZj/vXnu5mf2tmb3DzE5K+t+dM8ybXMxjO8t+3WDbn1Uys71mFszseWZ2wMyOm9lPm9m1ZvYlMzthZm90y15iZv9sZkfN7IiZ/bWZre/Z7hfMbMbM/sbM3tPzPr/PzG7rrPdTZnb1af7JgVMSQjgk6cNqf7HKzEbN7HfN7F4ze9DM3mRm48vxZvYDnWP3pJndbWbf3Xn+AjP7gJkdM7O7zOwn3TIvN7P3mtnbO33iDjP7Fvf6i83s/s5rXzWzp3TW+xJJP9w56/XFTuzNZvZqM/s3SfOSLu49e9R7xtjMvrXTz050+vdzzewFkp4t6Vc66/+HTmx3XZ2/xRvM7IHOvzeY2WjntSeZ2X1m9iIzO2xmB83seWf6/wdYltJX3fH5ks531D4ze/byujrfvX9iZjeZ2ZykJw9Y32Yz+2CnDx0zs09Y54enDf6e7tv3zeyvJO2W9A+dPvgrnef/xtpnuafN7ONmdlXnefrsGcLgd/U8QdKYpPf5J0MIs5JukvRdg1bQ6Vj/IOmLknZKeoqkXzSzp7qwH5D0t5LWS3qdpJvVHmAve46kd4cQ6kPu93WSLpP0w5LeIOnXJN0g6SpJzzSzb1/ePUmvlXSBpG+UtEvSyzv7PSLp/0p6m6SNkt4l6b+59/VNkt4q6ackbZL0p5I+sNxBgbPJzC6U9D2S7uo89VuSLlf7C/ZStfveb3RiHyfp7WrP5qyX9F8k7ess925J96ndJ54h6TVm9h1uU/+1E7Ne0gckvbGzzisk/ayka0MIayQ9VdK+EMI/SXqNpPeEEKZCCI9x63qOpBdIWiNp/4D3t0fSP0r6Q0lbOu/rthDCmyX9taTf6az/+/ss/mtqz1hdI+kxkh4n6aXu9e1qz2rtlPR8SX9kZhtW2h/gVKX01Y7tkjZ3nv9xSW/u9LdlN0p6tdr96JMD1vcitfv3Fknb1P5hGob8nu7b90MIz5F0rzpntkMIv9OJ/0e1v4e3Svq82v1U9Nkzh8Hv6tks6UgIodHntYNqd6BBrpW0JYTwyhDCUgjha5L+TNKzXMwtIYT3hxBaIYQFSX8p6Uel7jTOj0j6q4T9/s0QwmII4SOS5iS9K4RwOIRwv6RPqD3lpBDCXSGEj4YQaiGEhyT9nqTlgfHjJVUk/UHnjPf7JH3WbeMFkv40hPCZEEIzhPCXkmqd5YCz5f1mNiPpgKTDkl5mZqb28fm/QgjHQggzag9Al/vc8yW9tXPst0II94cQ7jSzXZKeKOnFnf5zm6Q/l/RjbnufDCHcFEJoqt0nlwezTUmjkq40s2oIYV8I4e4B+/62EMIdIYTGED9sb5T0sRDCuzr98Whn/4bxbEmv7HwGPKT2bNZz3Ov1zuv1EMJNkmYlXdFnPcDpOJW+uuzXO99T/yrpQ8qeHPr7EMK/hRBaan8HrbS+uqQdkvZ0jvdPhBCChvuezuv7fYUQ3hpCmAkh1NQ+qfQYG/5aIfrsEMgRXT1HJG02s0qfAfCOzuuD7JF0gZmdcM+V1R6ELjvQs8zfS3qTmV2k9gE9HUL4rIb3oGsv9Hk8JUlmtk3S70v6NrV/NZckHe/EXSDp/s4HQ7/93CPpx83s59xzI53lgLPlB0MIH+vMZrxT7R+sI5ImJN3a/m6V1J7lWM4H3KX2zE2vCyQtf2Eu2y/pW9zjQ649L2ms8/lwl5n9otpfcleZ2YclvTCE8MAK+97b71eyS9KgwXSeC5Q9s7xf2X56tOfzbV6dzwjgDDqVvipJx0MIc+5x7/Hr+9GWAev7P2r30Y90Xn9zCOG3NNz3dF7f/7qTY52TVq+W9N87+9TqvLRZ0nRvfB/02SFw5nf13KL2L8mn+yetfZXq96idniC1z65OuJDtrn1A0j0hhPXu35oQwtNcjB9gKoSwKOm9ap/9fY7SzvqmeE1n248OIaztbG/5E+OgpJ3mPkHU/gJedkDSq3ve10QI4V2rtK9Ars4ZobdJ+l21f5QuSLrKHZvrOhfbSO1j95I+q3lA0kYzW+Oe2y3p/iH34Z0hhG9V+4s0qH2hrNTTv/0iPY8HfY702+eV1r/sgc4+LdvdeQ446xL7qiRtMLNJ97j3+PXH/4rr65yJfVEI4WK10xheaGZP0XDf0yu+rZ7HN6qdzniD2ukJezvPW058L/rsEBj8rpIQwrTa0w1/aGbfbWZVM9ur9sD0iDo5PJJuk/Q0M9toZtsl/aJbzWclzVj7YphxMyub2aPM7NoBm3+7pOeq3UFXa/C7Ru3pkmkz26l2DuSyW9Seyv1ZM6uY2Q+onXe07M8k/bSZXWdtk2b2vT0DB+BseoOk75T0aLWPz9eb2VZJMrOdLn/vLZKeZ+0L0kqd174hhHBA0qckvdbMxqx9AefzJQ0sU2ZmV5jZd3Ry3hfV/gJePtvzoKS9Nriiw22SntX5nPkWtXOOl/21pBvM7Jmd/rjJzK5x6794hfW+S9JLzWyLmW1WO/9x1UqvAUMYtq8ue4WZjZjZt0n6Pkl/02+lndSH3PVZ+yLtSzsndabV/o5r6dS/p5f19sE1ap84O6r2D9rXDIjvRZ8dAoPfVdRJXn+J2r9SZyTdo/bBfIObivkrtRPl90n6iKT3uOWbanfWazrLHlE7j3DF3J8Qwr+p3Sk/H0JY8WKY0/AKSY9V+0PgQ3IX9oUQltQ+4/18SSfUPiv8QbU7tEIIn5P0k2on/R9X++KF567SfgIDdXLj3q72F8WL1T4mP23tKiofUycnrpNC9DxJr1f72P9XxbMsP6L2WZoH1L7g82UhhI8NsflRtS+0OaL29OhWxVJOy1/UR83s8yus49fVPrt7XO2++U733u6V9DS1L9g5pvZAeTnn8C1q5xqfMLP391nvqyR9TtKXJN2u9sU3r+oTB5wVw/bVjkNq94kH1P4R+NMhhDtXWP1K67us83hW7RM8fxxC+JdT/Z52Xqv2YPWEmf1S573tV3vW6D8kfbonnj57Blg2LROrqVNS5JWSntj5QlrNbf2zpHeGEB4Wd3Azs89IelMI4S/O9b4AAM5v1r7j2TtCCBee633Bww8XvJ1FIYS/MLOG2mXQVm3w25lueazaeUPnROfChK+q/Sv42ZKulvRP52p/AAAAJAa/Z10IYbVycCVJZvaXkn5Q0i/0XHl+tl2hdn7zpKSvSXpGCOHgOdwfAAAA0h4AAABQHFzwBgAAgMJg8AsAAIDCOKs5v2ZGjgXghBBscNS5QX8Fsh7O/fW6H31dUn/d+K/p11yHWi0pvnnsxOAgp/Soy5LiJcnqzbQFGmnxjc1p5edn9o4nxUvSyGxrcJAzv6U8OMjZ+tGUG0K2Le3ZnBR/5JqJwUHOjnfckRQvSY0r9ybFf+yTL83tr5z5BQAAQGEw+AUAAEBhMPgFAABAYTD4BQAAQGEw+AUAAEBhMPgFAABAYTD4BQAAQGEw+AUAAEBhMPgFAABAYTD4BQAAQGEw+AUAAEBhVM71DgAAgNNjzdXfxv978eVJ8Zf/5h1pG7j3YFq8JJuaSooPayaS4huTacOkjZ84kBQvSc23p8VP/tB8UvxXfjPt/02SvuGldybFt775qqT4gz+aFi9J6+6pJy+ThzO/AAAAKAwGvwAAACgMBr8AAAAoDAa/AAAAKAwGvwAAACgMBr8AAAAoDAa/AAAAKAwGvwAAACgMBr8AAAAoDAa/AAAAKAwGvwAAACgMBr8AAAAojMq53gEAAHB61n/5eFJ86/iJ5G1c+quHk+KbjUZS/KFfeEJSvCTt/NDBtAXufzApfPa6zUnxx67ckxQvSetfV0+KH5v/UlL8ps+nn+dsLSwmxe95+teS4mu/vCUpXpL02dvTl8nBmV8AAAAUBoNfAAAAFAaDXwAAABQGg18AAAAUBoNfAAAAFAaDXwAAABQGg18AAAAUBoNfAAAAFAaDXwAAABQGg18AAAAUBoNfAAAAFEblXO8AAAA4PYs7ppLiRyt7krdx97PXJ8Xv/JdGUvz2P7glKV6StHlzUnjt2suS4je9+wtJ8TY1mRQvSeHCbWnbWL8uKX7DnfNJ8ZIUarWk+PrPb0iKL8/PJcVLUjN5iXyc+QUAAEBhMPgFAABAYTD4BQAAQGEw+AUAAEBhMPgFAABAYTD4BQAAQGEw+AUAAEBhMPgFAABAYXCTi7PAXDsME5QnZ+G8RUNeUO96htjBobZxOlZ6/2dsIwAAoOg48wsAAIDCYPALAACAwiDtIVXO9LytMDVfVrnbbrq7Uwe/rqFyI+JvFR9ezcS0uq26xaiw0g5mtt3/91DJrdfL3Gt7qPeQE79i2kP/9x1y9gkAimb0yEJS/ANP3pC8jb0fmE+KH7nrYNoG9uxKi5d08rE7kuIn3v+5pPjGE69Oiq8emU2Kl6TS9FxSfPPYiaR4e/BwUrwkldasSYo/ecW6pPip9346KV6S7vvVJyQvk4czvwAAACgMBr8AAAAoDNIeEvnsAZdVMKBYgUt1yKwsbyOuXYopE9ZyL7T6T/mbXzi4rQ37M+dMpS6EgU/nr+frAklvAAAAZwZnfgEAAFAYDH4BAABQGKQ9DCGTheBfyJnDX2mSvlyOa2v6HAq/Lr+CRv/qEKVSqW98c5idGuaGGj2ag0NO72YUQxaj8H9//5a4DwYAABgGZ34BAABQGAx+AQAAUBikPSTy1RSCm2xfaQreT9s3mzllEHLiS2V/o4r4fKvpbmaRs6/D30TD/QYKOYkFw1SmyGw8Z/3DVm4gjwEAAKwCzvwCAACgMBj8AgAAoDAY/AIAAKAwyPkdgk8/zSsllkmV7QkJOWm+pczzObnELke4VI53e1PmrnFu45VMYnDffc3urOR/AyXfjS1vAYvrDJnt+fxin/+bnwucVwWOtGAAaFvaNJ4Uv+W2xeRtVGaXkuJPfNvepPi1X5lOipek45eXBwc5azauT4p/4Lq0v6u10uIlaesX0v4vyvvvS4q3b74qKV6SdMfdSeEPPGWogqhdV358W1K8JG35Yt4VTuk48wsAAIDCYPALAACAwiDtIVHI+72QqebVM4XvUgMq7s5s1ohxJRdUdivzEwn1VowpVUfj5uo19V2g7FMgVkoSGLL8WD/D5B4MlUuxwjJ+cXIdAADAaeDMLwAAAAqDwS8AAAAKg7SHYeRVN8hMzQ9xNzRJDZfqMOqeH1e8YrXicgMaLqbuqiO0Gu6V/kUgpLy7yZV60hxC36ayv41cu5VXHcL/Dfq3LSdtIazwNxvuLnLA6vKHYdVcf3XtlsvLqYfYGVt5VWI4iAHgrOPMLwAAAAqDwS8AAAAKg7SHVMPc+aG3JIHLABhxT69ziQ9Xb7io2/4f3/WMbvv33vO6bnvG/VZZbMW0h4qrLtFyeQ++HPRJd6OJaatm96+aUyQ8c3cJl0/hthcyN6rIlLzoux4f4aeRG8PO/oacbQCrYMylNGytjHXb10xu6bav3R4LyB+bm+22bzm2v9u+b+lkt73kKr7MNRe67Vor9tjgPkOaYaXi8aF/2/JuJgMA4MwvAAAACoPBLwAAAAqDtIchWGbavv90ft7kvySZe2bCta/fcEW3vWM6Tq8+5v6YHPH+x/9Gt90su5tfuKlQczewqFXinpwcj8+/4KN/0G1/wSazOzjh6k74sgtNlzjRcPdcb867+P7pEHkVIXyChbm/Wqkn7SFTtEI+TcP/dX1iB1O7ODMmS7E/XFie6ra/qbq1237i6KXd9nVrL++2pzav77Z/4uJ13XZtbCK2p7/SbU9b7Ev3j8ZjeN+muA9/8qUvZ/ZvZiGmSjTdR3gYWdNt22xMs2hO3xNjlo7KPXBrpf880s3uHBkc5Kzdv5i8jdLxmaT4hU3rBgc5jcduSIqXpD3vvi8p/sSTLx0c5IzMpFVk2f7B/YODepXSzkPWr390UvwDT5gYHNTjgurlg4Ocb3zpvqT4xkXbk+IlaWS6PjhoSJz5BQAAQGEw+AUAAEBhkPaQKHOviEw7TuiXe0pC+AmH67d9Y7c9eSxWbNjUistvn4tb2bDkEgWW/NXc7r/OpT00q7F9rBqnCF77/S/rtm/+zmsy+3f71rXddrUap1ttMU6dbmjNddtv/Znnx4X91GkjTsdqKU7nlpr9pyoyxSR6pl2zj3JutpFXXQJIUOo5B7C2FNNs9pZjitBOG++217i0nrUuNWKiEtMebHRzt92YiDGjuzd220vl2Dd2TMUesXNDXP++H3p6Zv/+oxE/H466dIqlibh/1X21brt294kY85W7u+36Xbd12zN3/3ncQCYdAgDOP5z5BQAAQGEw+AUAAEBhkPYwhGwZeVdxwT3fcgkR4z1pD49bE29gsXUuTs9XmzHtoezSJkIpToW26q4iQjlOx7aarppCKW7bLLbXNGN7tBH/q+fHd2b278GpTd12oxH3qTQep2cPuyPliW/7eLddb8R0iN3lmOrwtzd+l9vX425r8f00farC15fIcIu4v3SmYD+pDjh91vN4Yyke7Ntce9wfe/WYVmCuj/rSMFbyKUuxXT8Rt9ioxOdd11Pd3VyjumNHZv8m3OdAbSreeGNpND4/tdl9PjwqLjtyQ7whR2vft3fb//5LH4rPL9zrtpZ2pTsAPBJw5hcAAACFweAXAAAAhUHaQ6Jm5lH/3w7lnuc3V+KV3uXjs932WCVWVghuar/ZiNOoDRczW4lTnIuuOkTFXfE9NxfTEEZH45XqR0NsT5djMXxJWhiN1R6WLO5HCHHKc9q1y5PxsGmEOP07OueKjZdiwfWgOJ+b+fv5P1Pv3HOmrIa/eYYP6n/DESBN9uBZ41IdRtyB2HRH72KIqUlLLn2ptOQrJcS+0SjHSgyLJ+LNBWru2D42Hrd1aDamMNxzr6uiIukhV9FlYbNLhVoT99sW47qqLZf+NBH75fq9sTJFZWOsQrN0/wG3NToWgPMPZ34BAABQGAx+AQAAUBikPaSyvKn2+DuitwZBbTFOc641d/91lwNQdv8V1VJMUTjeivH3T8Wi+cfHYurCwlKc1ixNXRDXU477dM/amD4xHbL/7fOzcf+qI/G14K5u9ykQrVac5rWQ8/vJ3PTvSukN3Q2s9JiqDlg9K93kYtTd9CWEmLpwohpjbluK6Q0uA0mtSlzvoqvCUlp3Rbc9X40fAidHYr86Ph77T202fh5IUnNLTHlqrXXPb4rrmm64zxnX6eaqsT0bXOrUtid120sP3BwXDfGzAQ9vm/79SFL84SduHhzUu43ahqT4E1elfXZf8t5TuMHKYm1wjFN/7rGk+DVvXD84yGltWDs4qEdpenZwkNMcLQ8OcrZ/emFwUI/S7XcPDnL2vfAxSfF733c0KV6SdDjt/24lnPkFAABAYTD4BQAAQGGQ9nA6MikQ+XP7ZXf1eCu4XAeLy9QUp1fvc6kHi+5GEy/51Ie77Uc9/ulx0+U4LVNfiOusluN69p1w+6PsNM4mV1y/5Noum0KNWLBC8+7q9kolbqMkPxWTmKpwKheVcyE6zgDr6a/mbiJRt9g+2XKpTe4GMvON2HfHajE1wix2mqV6TFMqt2JMrRQP4iWXqTA/F/vYyBGfwiCNuHQFX+Gh6dKcGu49lUrx+dFRVwWiGfuoNf3fIG1KFQAeaTjzCwAAgMJg8AsAAIDCIO0hkbmpdjebqKarjFDqnTZsxdcqbho1KLYfcu0vbolTpG/84Ee67bvKF8b92HZZt70UYhpDw13lbS6tou6uDn3wn7NXTNbHYpyFON06MzrfbV/6tN3dds2lOvjUg7ExlxsR3FStz4Awf8j5tJFsmkReUQiPrAecCaHnYDN3M5mlUizfsNCK6Q0txQoM+0LsryPNdd12ZSn2y1CKz4/X4zpbro823QXZ9cWYHjV1KHuOYmE+Ph5xKVINt3zNVZ1w2RBa654fW3A3rin7z434WRHoZADOQ5z5BQAAQGEw+AUAAEBhkPZwGlw2Q2aavrfOQdMVyp+vx+nFpRBTHRYnY1WHV930oW774PjWbnt6Ik6jHqzGqdaaq97QqMR5zXLZXRXudnbCsr95GrOxsPioq0xRKcV9HXNvqhZ3W24Tas24lQaf+uG2l5ljdukWPX+10gqPuttzyzA7i1PVW+2hUY3VGGZDTIGom2/HtIeDin2u2nLtZmyXmnGdG0P8PCi7KjHWivvhq8KsP+oqxEhSLfatJZeyVJuNvaC2xaVauc6xNr4FVWfieqsl34M4JwLg/ManHAAAAAqDwS8AAAAKg7SHRCHn90I5MwWfrfaw4K8eH4tToScspivcczLen3xmalNcdtTfJzyud7QaUxLqSzEPoVqJMRWXntB0+72wtJjddzfj2WjE99GsuqL5dbcudyMMfzV4Se6FvHIN5laUWbYnLPNomN9oiTfVADpGy1OZx/sXd3Tbh2xLt11v+gomMe1o4WCsnlItxf46MbKh214zHtMeJtyBX3HlYyYsHvUT7pN5352uRIOkZiv2s7W3x5SlNetidZb918T31FqM27DR2J5a41Ij9n81biDEzyI8ctR2rB0c5Gz91NHkbdji0uAg5/IX3pkUX5qaHBzUozkzMzjIOXnrxUnx5fVpSXXjn7w/KV6S7nzFVUnxl7/ktqR423VBUrwktRqNwUHOnr8/NjjImd+ddrxK0uTs/OCgIXHmFwAAAIXB4BcAAACFweAXAAAAhUHO71BKOW3P5/yOZl45WI9/5unZ+PxsNT4/Mx5znWqVmFvYcKXH5Coe1RZiXt5INeb5Nl26sU/ZcVXLvo5Z//Jja+djrtOjDsWIkHPUrHW5jB/2aYO5+b+x2epJq/J/5bxsXsqb4UxY6rm7YKMcc/SDK0e45A58n9fvsyCb7qD0pctKjfhC3eflu7KDI6X4/Ji7feRkI9uByq7jbHM9Zb3r/OGQu+Oky/mdKLuSh5X4AWG1I3EDoae0GgCcZzjzCwAAgMJg8AsAAIDCIO1hKIPLaLXc74jZnrSH/Y118bVSLJFUL8USRk03/Wn+tmlNXxosTneOuKnTpisfNj8fpzKrk3E//N3oGo2eaU2Lh4G5wAvn4j49+V9i+O75hW675JIPptfHMiRvacVlT+alPYS+TUlS0y9jOX9/P11NDgSSxAOs2TPNXy/F1xoudWEpk78T+0zDlfhrhVhGsKzYLyuuPFnLde/gtuVvfujbkz2fP75U2g7X3tCMcVMH47bLLu1hzO9Hfa7bbtYOuC2Q9gDg/MaZXwAAABQGg18AAAAUBmkPydxV1O6K7FbL/47IllaYVrx6vDUe7xjlKzMoxOnI0PJlGtz8p5vWdLOxWlqM05djY+tdTAyq1+M6S63sf3up7FMo4vuYqsXp0m+Im9DVR9wdo9x6DuyIz/t7t5zMSxvJS4dYKY70BpwRLt2g5xxAy1zHdP0h87xiFYigxb7tVss934ppCKHkK8P49Iu49mYzph6MV7IdZVMlLr/FVW9Y69IVdrgbIZUXYozVYsrS/MIJt3+uTScDcJ7jzC8AAAAKg8EvAAAACoO0h2H0vweEWiGvCkT2N0Vw06VNf+cJd5V5ZSxOozaDK1bv11X1aRZxPeURt3439bngblIxOhFTMZpL2WnNkru03NfTX2zEqdpxV8CiUvLTvzGmZHHb5lMdhkpbWOF3WNNVwshd1eCKHEAUj5dqZTLzylIzHuwli681y+7j0uLRV67HtKaqTXXboy7taKwU++sh9/y6Sjy2x117Mn4c6MFm9mO6VnP9zN1hY3057vfESHxh1OK2JzfFz4GqS8Fa3P+Q2wJ96ZGoXEur0nHPMzYnb2PXR+cGBznVZto+hfnFwUE9Snt3JcVf9NtfSopvLaTt08lnXJsUL0mXvugzSfF3/nHaNrZ/PP08Z7hua1J8eWlwjLfmP2fSFpA0e/WO5GXycOYXAAAAhcHgFwAAAIVB2kMqy2lnbriQnTYMmTg3Wd+K7apLJWgs1mLMhC/rEKecRqvxcu6GX2eIy06Oxptr+HtlKGSncYLbj/JIPCQmxuPzi7OuGoVbmVX6p2jkXjE+bOWGENdVzgnxf2WuT0caX+0he/T4G080QzzWW6H/FG5wR2IIsWqCNWM6hMsO0mg99r9qiGkIcyH2vVmXvlTrSVMK7kY04yPxtSmXNlGqxRgXIl84IizEPm25vQwAzj+c+QUAAEBhMPgFAABAYZD2kMrPteemQLiKDr3KcZrT3NRmw994YnSi/wYtXh352X98i1unuzS8vKbb/Oan3NhtNy1ut1yOhe4lKZgvuu/LWcT9G62Mx90oxX1tWGzXzB9OQ9zBwoe08n+HtdT/70mqA86E3nSGUHJpR63YV4JlDtjYdFVOmjrSbdczIXGdrfqe+EIjVmgYKcV+bNV4zC+1/OeBtOhTF1wnKrmqDhWXClVxMRWXTtRwV2dP2oZueyYcdVujlwE4/3DmFwAAAIXB4BfCnQdNAAAK/klEQVQAAACFQdpDqrxZQH+xdKu3SLx77Col+KvKMzHuBhaquxSFavzvMndld6i7YtGVuP5bP/oOt98xbUHz2bSH0Vacbh1zBfVHm3Gf1lz/C/EtNNw0b4jLloI/nHJ+V+UWgchPFcksMmy1CGBF7vi0bIqOlXwaUKNvnJm/WU1MacgUc3GrbfnqDY173fpjvzzhU5OCv2HM+sz+LbjUqZpi//M15kcqroKLu8lOyX9uuOyOTeULu+0HW3e7/aOTATj/cOYXAAAAhcHgFwAAAIVB2sMw8mb+/POZTIfsbwrzgRbTEqpuCrLsFqn7CUx3E4nsBeZx2tXfIKPVjAX0m6Vj3fbYfNzA7kb26vHtbgb31d/zczFuNk7JbnOZFWV31JSrcdtVN+dr/tDyb9+1Vyqrn7n+PlNVw/9t/Y1FVlgZ8HXiAVOyqcwr9Yo7dl3uQitTxcXdKManKbl0hdDyR3HMMViajdUUKoo3wmjapNts3Ienjl6Z2b9dpVjRZcNSXCa4iiyj62O74j5nfLesbojbLrmbc9CZHpkWto4ODnJ2v+ozydsojVQHBzlh3dqk+H0/dVlSvCTtef0Xk+IfetbVSfHlpcEx3oY7Z9MWkBRCWp+77O21wUFO5WsHk+IlyWyIik1O2LR+cJDT/MpdSfGSNDZ6VfIyeTjzCwAAgMJg8AsAAIDCIO0hkS/QkJ2pcFdR90wbVitxijSE+W670YjT9vU5t2I/tdTyl4+7bbgbTQRXQWLM5U9ULE6NrG/E9f/6jT+W2b/dM3GKdNeJ6W57fG6u226W4xTp4kTcRsntR200vs+8G1N4K030hLwbiABnRDyoytXsdHHJfyq6gzT4tCNXQSGYmxf1MZmbZ8QYc7k/JXegW+YzJLZnmg9m9m+6Ffv1SZeKMeZi5l1WhrX8VLW7yYVb9oKR3d32HY0vuf3I3gAEAM4HnPkFAABAYTD4BQAAQGGQ9pDIZyHk33Ch7h8oNB6KbTdlWSq5qgvVeAV3019dWvZTsi6VYCnOa5YaceOj7grztW6e9or1G7vtj7znTZn9m3IXjk65ovtl9wbHFff1mU95VoypxP07vDZexV6Tu5GGTxVx282t6NAr83fuvYEIcCrikbi09FDmlUr9mHsU+0Nwx56Zq5Qw4Y7qpksJcje7MVeFpVwd6/u8Wi4lqhnXebAR048kqRbiZ0WjtLXbnm1s67YPL8W0jKlSTHuYLMf2rNvekVbsu9zYAsD5jjO/AAAAKAwGvwAAACgM0h5S5U3P+zIQrWxV7MW5A+5RnEZVaV23WVYsEF0ux3amTr67qnykEqcmxytx27vWb+q2p+ZjfKV+vNtu9kxrLrh1zZfjdGkp+CnceKi8/hO/H5ddiiketyoWG8+kPeTNouamjfQIOW3glMUDqVk/mXmlPnt/fGAxrSdb7SGmD1THptzz/qYYcRutRuwnNuKKwYfY35rNuGzN3TjjUCOb6nMyxBSkGcV0pkOlnd32fOtwtz3iOpq5N3EkxMouX2v+Z9wlkVoE4PzGmV8AAAAUBoNfAAAAFAZpD4nMF73PTNu7/ATLVnuwcMI9momLuKnJ5rwvRO/L1fuNxG3UXOWHmpvCvd1dGL7BreeazVfGF3qK+rdqbkrWpVC0SnH6s1GJ2/vykf+Iz7v11FRzbXcVe16FDHfTDuuZavW/yrLF/93ibhmyIZAmHjEhZG/IsnDyq922v5mFlUa67ZKrwlI74DqdxWO1XIoxZRdfXoz9su4+Nhohrr/sjvlq2JzZv+lWrEZxRPEGGOPhvm77WCumbjRcv1wMMR1prhXTHuZdCgQemSbvmx8c5Bz6meuStzEyk/ZJO3407SYpe9/74OCgHs35tPc9d2HaXZN2v/KWpPj9L7s+KV6SLpq7PG2Bh04OjnGOPvWStPVL2vjeLyTFLz5mV1J8ads1SfGS9ODjRgcHDbv9M7YmAAAA4GGOwS8AAAAKg8EvAAAACoOc39Ph05/8z4ieHEL/Rw4uF9aXHMumxfb/b8mUICr1L0dkirnD862Y33frkc+5/an2LBN33ufRNt2d6nze4JLL9G34klGZvN2cckmh/++tcs/jUs6j/CJMlGfCqco/dvxd3UIzHvehtdg3xie1B1easFmPecFmI32ipZq7iMD3ybrN9uxUpv5ht1VuxvUuKl5n0AhuP1yfbrlrCChvBqBIOPMLAACAwmDwCwAAgMIg7SFZzu8FP51v2bSHui8IlqkUU+rbzoT42mo5qQ5+xrLppkQX/NSp4tRn2aUwrLAqtTKFzJo5UTmGqSbj3lpvQRz/Nyhn9sP/zZiqxWrrf3vBbKpDzpK+LGLmBX88D779YStk+2vIlPjLrSPoWr53URQQADjzCwAAgMJg8AsAAIDCIO1hKP3TE3KtNLOYuSvcMNvOuUNO/9nYbIjFqc+6S4dorHR1u3/glrdh9jUv1cHd9So7S+umb3vWT1UHnL+GOYZjh2iskKaUtwwAIB9nfgEAAFAYDH4BAABQGKQ9DMVfXZ0j76LrFRcaYvrTLztUeMs/GBwz5LaHmlDN+xvkXRm/wkqHedtM8qIYONIx2NKG0aT4nR84kLyNxo4NaQt89o6kcNu6OW39kip7diXFb/tcfXCQU77s4qT4scNJ4W0HH0oKX7rmoqT46lx6uqCNpR1PJy4ZGRzkbP2TW5LiJWn0sscnL5OHM78AAAAoDAa/AAAAKAzSHpIlpiqc0/Wew8oIZ3CmlklfAABwpnDmFwAAAIXB4BcAAACFweAXAAAAhcHgFwAAAIXB4BcAAACFweAXAAAAhcHgFwAAAIXB4BcAAACFwU0uAAB4hBu/44Gk+DA5nryNyqETaQvs3JEU3ti5MW39kspfPZAUP3pTWnzj+quT4hc3J4VLkprHj6dtY9PlSfHrPncwKV6SmguLSfHbPjOdFH/k+Y9PipekykLyIrk48wsAAIDCYPALAACAwmDwCwAAgMJg8AsAAIDCYPALAACAwmDwCwAAgMJg8AsAAIDCYPALAACAwmDwCwAAgMJg8AsAAIDCYPALAACAwqic6x0AAABnV/M/v5a8TPmSvUnxrQ1rkuIr+w8nxUtSCK2k+PKmjWkb+PI9SeE7Ry9NW7+kh/7n9Unx228+khTfWjuRFC9Jpem0ZZq33pEUv3Xh8qR4STrwvZuTl8nDmV8AAAAUBoNfAAAAFAaDXwAAABQGg18AAAAUBoNfAAAAFAaDXwAAABQGg18AAAAUBoNfAAAAFAaDXwAAABQGg18AAAAUBoNfAAAAFAaDXwAAABRG5VzvAAAAOD37n7M3KX73+8aTt3HTzX+XFP+93/qDSfFHbrgoKV6S5rdZUvy2WxeT4ktLraT4I48aS4qXpO1vvjUp/it/9Oik+CtffjApXpLmH3dJUvz4PceTt5GqdQZHrJz5BQAAQGEw+AUAAEBhMPgFAABAYTD4BQAAQGEw+AUAAEBhMPgFAABAYTD4BQAAQGEw+AUAAEBhMPgFAABAYTD4BQAAQGEw+AUAAEBhWAjhXO8DAAAAcFZw5hcAAACFweAXAAAAhcHgFwAAAIXB4BcAAACFweAXAAAAhcHgFwAAAIXB4BcAAACFweAXAAAAhcHgFwAAAIXB4BcAAACFweAXAAAAhcHgFwAAAIXB4BcAAACFweAXAAAAhcHgFwAAAIXB4BcAAACFweAXAAAAhcHgFwAAAIXB4BcAAACFweAXAAAAhcHgFwAAAIXB4BcAAACFweAXAAAAhfH/AfKvvE0J5qnIAAAAAElFTkSuQmCC\n",
224 | "text/plain": [
225 | ""
226 | ]
227 | },
228 | "metadata": {
229 | "needs_background": "light"
230 | },
231 | "output_type": "display_data"
232 | }
233 | ],
234 | "source": [
235 | "f, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(12, 7))\n",
236 | "\n",
237 | "x_mu, r, kl = model(x_c[scene_id].unsqueeze(0), \n",
238 | " v_c[scene_id].unsqueeze(0), \n",
239 | " x_q[scene_id].unsqueeze(0),\n",
240 | " v_q[scene_id].unsqueeze(0))\n",
241 | "\n",
242 | "x_mu = x_mu.squeeze(0)\n",
243 | "r = r.squeeze(0)\n",
244 | "\n",
245 | "ax1.imshow(x_q[scene_id].data.permute(1, 2, 0))\n",
246 | "ax1.set_title(\"Query image\")\n",
247 | "ax1.axis(\"off\")\n",
248 | "\n",
249 | "ax2.imshow(x_mu.data.permute(1, 2, 0))\n",
250 | "ax2.set_title(\"Reconstruction\")\n",
251 | "ax2.axis(\"off\")\n",
252 | "\n",
253 | "ax3.imshow(r.data.view(16, 16))\n",
254 | "ax3.set_title(\"Representation\")\n",
255 | "ax3.axis(\"off\")\n",
256 | "\n",
257 | "plt.show()"
258 | ]
259 | },
260 | {
261 | "cell_type": "markdown",
262 | "metadata": {},
263 | "source": [
264 | "## Visualising representation\n",
265 | "\n",
266 | "We might be interested in visualising the representation as more context points are introduced. The representation network $\\phi(x_i, v_i)$ generates a single representation for a context point $(x_i, v_i)$ which is then aggregated (summed) for each context point to generate the final representation.\n",
267 | "\n",
268 | "Below, we see how adding more context points creates a less sparse representation."
269 | ]
270 | },
271 | {
272 | "cell_type": "code",
273 | "execution_count": 188,
274 | "metadata": {},
275 | "outputs": [
276 | {
277 | "data": {
278 | "image/png": "iVBORw0KGgoAAAANSUhEUgAABIAAAAC3CAYAAABqmCVcAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzt3XmcXFWZ//Hvqarel3QnnV7T3dl3CBDWAG4jgyIyjtsPB3VEnGFcUWTG3UHEUUZFRweccRwFRUUUZVdUFMfIFgIBCdmTTtLpJJ2l972r7u+PLmcCL3ieFprq5ubzfr36Bclz8r23qp57zq2T6k6IokgAAAAAAACIr8RknwAAAAAAAABeWGwAAQAAAAAAxBwbQAAAAAAAADHHBhAAAAAAAEDMsQEEAAAAAAAQc2wAAQAAAAAAxBwbQDESQlgfQnjZZJ8HINGPmDroRUwV9CKmEvoRUwW9iKniaOjFF80GUAjhoRDCwhDC3BDCI89Q/5sQwsMhhN4Qwt4Qws9DCGdMwHGvCyFc+XxzslnvCCGsnoisZxJF0bIoiu4d57m0hBBeORHHDSG8L/vcD4UQrpuIzKmOfvRNRj+GEApCCP8dQtgZQugJIawLIbz6+eZOZfSibxLnxhuyz3l3CGFzCOFdE5E7VdGLvsnqxSMyF4QQBkMIN0xk7lREP/omcW68N9uHvdmvTRORO1XRi77JnBtDCOeHEDaEEPpCCNtCCGdOVPZUQy/6JnFe7H3aVzqE8PWJyH66F8UGUAghT1KzpC2SVkp65Gn1SyV9VdK/SKqR1CTpWkl/ldszPWq1SbpS0rcn+0RygX6c0lKSdkt6qaRpkj4p6aYQwuxJPKcXDL045X1e0uwoisolnSfpyhDCykk+pxcEvfiicY2kNZN9Ei80+vFF4X1RFJVmvxZN9sm8UOjFqS2EcJakqyRdKKlM0kskbZ/Uk3qB0ItT2xHzYamkWkkDkn78Qh1syn9JOl7Sb7P/f5Wk9xxRmyapV9KbjD9foLGGbst+fVVSQbb2Mkmtkj4sqV3SXkkXZmt/L2lE0nD2GLdnf79e0s2SDkjaIekDRxzrLklfPuLXN2psY2SJpEFJ6WxW57Oc670ae9PwkKRuSbdKmn5E/TxJ6yV1ZscuOaLWIumV2f+/XNJNkr4rqSf7Z07M1r4nKaOxxuqV9E+SCiXdIOlQNnuNpJo/83W6UtJ1k90v9CP9+LTH8LikN0x239CLR3cvSlqUfQ7fPNl9Qy8enb0o6fzs8S6XdMNk9wz9ePT2Y/Y83jXZfUIv0ouS7pN00WT3Cb1ILz7t/P9WYxuR4QXphcluRufBX5h98vqzL3anpNHsC9ApaY6kV2V/L2XkXCHpAUnVkmZmL/bPHtGwo9kxeZLOyR6vMlu/TtKVR2QlJK2V9GlJ+ZLmZl+gs7P12mzjv0LSBdlaWbb2Dkmrncd8r6Q9kpZLKsleGDdkawsl9Uk6K3uu/yRpq6T8Z2nYwezjSWYvggeeqbmzv75Y0u2SirPjV0oqz9Y+KumOcbxesd4Aoh9fXP2YHVuTPe7iye4fevHo7EWN/e1Zv6RIY3/bVjrZ/UMvHn29KKlc0mZJsxTjDSD68UXTj/dq7E3fQUl/kPSyye4devHo68Xs2OHsmK0a28D4d0lFk90/9OLR1YvPcP6/kXT5C9YTk92U43wSfi/pOI19FG2djtgNyzbFPufPb5N0zhG/PltSyxENO3Bkw2cb7tRnadhTJO16Wv7HJH3niF+/QWPfhnJQ0hlH/P54G/YLR/x6qcYmp6SkT0m66WkXzx5lF85naNhfPy1nwGjYd2rsQj72ebxOsd4Aoh9fdP2YJ+nXkv5zsnuGXjzqezEp6QyNfUti3mT3Db149PWipH+T9JEjjhvLDSD68UXTj6do7NttCjT2N909kuZNdt/Qi0dXL2rsEyiRpIcl1Umq0tiG5Ocmu2/oxaOrF5927s0a+4TTnBeqF6bszwAKIUwPIXSGELokrdLYC7lJYx+j7wghfDA79JCkqhBCyoirl7TziF/vzP7enxyKomj0iF/3Syp9lqxmSfXZc+sMIXRK+rjGPmnwJ7drrME2RVH0XH5I1e6nnWuexialpzyOKIoy2bENz5Kz74j/75dUaDxP35N0t6QbQwhtIYR/zX6vKEQ/Pu1cp3w/hhAS2YxhSe8b7597MaAXn3KuU74Xs+eTzj7eWZLe/ef82amMXnzKuU7ZXgwhHCfplZK+4o19MaMfn3KuU7Yfs+fxYBRFPVEUDUVRdL3G3nSfM54/+2JALz7lXKdyLw5k//v1KIr2RlF0UNLVohefDb2Ym/fTb9PYBteOP/PPjduU3QCKouhwFEUVGvso1bey//8LSa+NoqgiiqKvZofeL2lI0uuMuDaNNdqfNGV/b1yn8rRf75a0I3sOf/oqi6LoyMnic5I2SKoLIbzFyHo2jU871xGN7X4+5XGEEEJ27J5x5h7pKecSRdFIFEWfiaJoqcYmiHMlvf055MYS/fiUc53S/Zg9j//W2CLyhiiKRp7D+UxZ9OJTznVK9+IzSEma9xz/7JRDLz7lXKdyL75M0mxJu0II+yRdJukN4Rn+BZgXM/rxKec6lfvx2bLDc/yzUw69+JRznbK9GEVRh8a+7evIvPE+zhcFevEp5zple/Fp3i7p+udwLuM2ZTeAjnDkTyk/XmPfL/i/oijq0tj3D14TQnhdCKE4hJAXQnh1COFfs8N+KOmTIYSZIYSq7Pjx/hOo+zX2fYl/8pCknhDCR0IIRSGEZAhheQjhJEkKIbxEY99r+XaNfaz16yGEhiOyZoUQ8p1jvjWEsDSEUKyx76X8SRRFaY39EKrXhBD+Irub+GGNXaz3jfOxPOvjCiG8PIRwTAghqbEfljWisR9s5QohpEIIhRrbpU2GEKyd0Rc7+nGK96Okb2jsh8S9NoqiAW/wixi9OIV7MYRQHcb+adnS7HNxtqS3SLrnOZzTVEcvTuFelPRNjW08Hpf9+g9Jd2rs4/txRD9O4X4MIVSEEM7+071iCOECjf3LS794Duc01dGLU7gXs74j6f3ZNbtS0ock3fEczmmqoxenfi8qhLBKY59EemH+9a8/iabA9yRaXxr7IUgnSZohaZsx7gKNfQ9nn8Y+qnWnpFXZWqGkr2nsJ5Lvzf5/YfR/37PY+rSsFv3f9/4t0Nj3SXZKuiX7e/Uauwj2SerQ2A/EeqXGfshii6Tzj8i6StIvNfY3G/nZ8zos6eCzPI579dSfWn67pKoj6n8t6UlJXZJ+J2nZs5z35Trie/w19rd/kbLfm6mxf9JvV/ZxXaaxNyabss/f/uxz9KexH5f0c+O5vzybfeTX5ZPdO/Tj0dePGtvRjzT2A9t6j/i6YLJ7h1486npxZvY8OrPn+0dJfzfZfUMvHn29+Azn/5Tjxu2Lfpza/aixuXGN/u8H0D4g6azJ7ht68ejrxWw9T2P/WENn9jn53+c3Tl/04tTvxeyY/5T0vRe6H0L2YJgiQgj3aqzRvjXZ5wLQj5gq6EVMFfQiphL6EVMFvYipgl60vRi+BQwAAAAAAADPAxtAAAAAAAAAMce3gAEAAAAAAMQcnwACAAAAAACIOTaAAAAAAAAAYi6Vy4O9et5l7vebRXn2KaW3bPcPNAHf1pZcMPd5n0dy/hyz3rd4ppvRV5t0x8xc02nWw552NyMzp96spwv880g++KRZj0aG3YxfZX4c3EETYNEVX3GbZO71e8x6dKjDPU66u9usJyumuRmjy+w+Cn9Y52akmhvN+pMfq3MzSrf500XpnoxZn/4H+zmVpPZXzHLHeKpuetysh9ISN+MXe6/JSS9K0mn/70tuP1b8vsWsj+fbedP77bkguWi+mxEV5Zv1xMEuN0PBfmrbzmtyIwoP270mSaNF9nFm3rnNzeg7ebZ9jEK/TcrvesIesKDZzbj7kc/kpB8XfnYcc+O/b7EHJPxTdXtx4Tw3Y6ixwqwXPunPN56t77HnX0mqetzvxb46ew1tuKPNzehcWWPWhyr8v9Or/rG9To8s9x/vPf/ziZz04vHvvtrtxdo7dpr1aGjIPU6mq8esJ+bY66ckZcoK7YzuATdDnfZ57H3TAjeiYvuIO6ZjQZ5Zb7i91c3oX2z3Yk+jf7/g9WJmjn8v8Mu1l+dsnT7+H8bRjz/fbdajYf8+OHPosFlPzPHXR+Xbr3Ho7nMj0rWVZr19ZambUbo37Y7prbfnxtpf7XMzhmfZ53rgOPv6lKSG69ab9cy8cfTjmtz04ylv/bLbi9N/t8usj2duTB+2318mlvtzUhhxemDU75HRqjKz3jO7yM3I7/XX6f6Zdi9W/8q+viVpuLnKrB88rtjNqLvB7sXRpbPdjF+v/qTZi3wCCAAAAAAAIObYAAIAAAAAAIg5NoAAAAAAAABijg0gAAAAAACAmGMDCAAAAAAAIObYAAIAAAAAAIg5NoAAAAAAAABiLpXLg43UVviDzH+1Xgqbo+d9HonCQndMZtces56sqXYz0lVlZr34t+vdjF1XL3XHVG6yH8+hVQvdjJnfuN+sd7zrNDejZtt0s953fKObkSsjCwbcMaMzy8165xn1bkbF9+znVSn/Ekw89KRZz5y2ws3orrV7ZOlndroZd679hTvmVX/1NrO+7+xZbkb1D58w65v+xb8mQuZYs941343Iqd6GpDumorjIrO9+vd+P9V9qN+tR6143IxodtetNDW7G4Bx7rqi/1e/H+ps73TF7LrDn6Y0fn+tmLP6Uff1tv2yZmzFYafdjyp+OcmakPOOOCaXFZv3Jj9S4GQv/wenFvXZdkvJ27LYzFsx2MzqPtXtx/n/4vXjDAz9xx7z1zPPN+paL/etm/pc3m/Wtl/lr/fBFdr8mB92InBktcm4IJSnYYzZ8YY4bsfBdD9sDDvtzjbZ32fXZ/v1P90vs+aj+9l1uRuWPet0xRX+db9Y3XzrPzVjwpa1m/cBxC9yMzrOX2APG8fLnUnj+bz+04Ypmd8ySj9trrDqcXpMUiuz7hUxlqZsxONO+b6y7w+/H5p8dcse0nGO/V9r4qXGs0/9sz42ZE51ek7T3AntuLD7gr425EtLPP2PzR/z1YuFnnfepu/x7xlBq91pUZt9PSNJoif1eafrv7XsBSUp/1x2ikjf0m/UNn/Wfs8Wf3GjWMyv9e8a9b7XHTNsx4mZ4+AQQAAAAAABAzLEBBAAAAAAAEHNsAAEAAAAAAMQcG0AAAAAAAAAxxwYQAAAAAABAzLEBBAAAAAAAEHNsAAEAAAAAAMRcKqcHO9znjsm07Dbr0XgOFIJdXzzXjUi07jfr6f3tbkbrO+eb9ZLFx7oZSz+7yx0z2rrHrM9c7TwfkkJevlmf8a373YxMSYlZL7hrjZuRK1U/L3DHJJ7YZNYr1gz4B3J68cB5C92ImQ8eNuvRg0+4Gb3vPsWst35ulptxykff7Y6pWGP3SfeHjnMzqr+fMesLv9vvZgxWF5r1yuvH0Yuf8IdMlOq1fi+ld7eZ9Yav73UzvPlz1yUr3IzmWw+Z9XCo083orasx64cXNfsZVza4Y4p2P2bWy7fWuRmZoSGzXn3KPv887ii1Bzz0RzdD1/tDJsKse+zrT5LSbfZjXvxBe/2UJO8oWz+13M2Y98Nusx722b0qSSFdada3Xez34jkfudQdM23vo2a9bLk9Z0lSpqfXrP/DuXe7Gbd84pVmvejWh9wMff1D/pgJULPGn+vTBw6a9UXvPuBmePPizr9b5GY03+z0/AF7HZek/J4ZZr31DU1uRtfVaXdM6WG7F+XfMirqt1+bi992p5tx+9+9zD6N++z5W5L0A3/IRJnxmH39SVKms8usL3qvv16kR0fNevt7V7kZ9XfY76W0w37fIEnDS5eZ9X1/P45+vMq/tyztWGvWi9uSbkY0YN9DrXqz0/OStl9qX+eJ1evcDN3oD5kIFU90uGMyHfa92PyP+e9jvV7cd4nfiw13Oveme/z7hd5Tqsz64aX+Ol3x5RF3TGH/42Z9xiP+52YyA4Nmvfn1292MoX+caQ8Yzz2jg08AAQAAAAAAxBwbQAAAAAAAADHHBhAAAAAAAEDMsQEEAAAAAAAQc2wAAQAAAAAAxBwbQAAAAAAAADHHBhAAAAAAAEDMsQEEAAAAAAAQc6lcHiz09rtj9l+00qwXdmbcjOm/bzXrmY3b3QwVFZnlRFmZG9H4xYeed8ZoR4c7JjW7yawPzpvpZ9yz1qwnjlvqZiS67dc3s73PzciVspZBd8yhN60w6wdP9ntx/g32cWZ8/xE3I1TNMOuJpQvcjNrvrDPrdTcWuhnRgP+cRScdYx/npnw3I9Nn90liJO1m5HWNuGOmlHFsxQ+//FizvuN1fsi8m0bNeuO/2nOWJKm0xCwPL5/jRkz/gT3fJKumuxlReak7JtTXmvUZTw75xxmyxxReMc3NSPbYPe13dO6EdOSOSZ9srwe732/3mSTVfNdeY+d+1O/FZI29tvWvaHQzym6z58aK1ZVuRrrenqMlKen04rSvl7sZXi/+8h2r3IziyO5F/9XPndGipDsmf/l8s77p4mI3o/lndn3WVQ+6GaGuxqz3nWafpyQV3bverDesKXAzRhfb94OSf9003T3sZnjr9F1vOc3NSKXte4qpNC9K0lCVf59UsMxe/7ZcYM97ktR4t30VVl97v5uhmmqzPLLSv2+cdtvjZr3iLv8tZDSnwR2TqLWvnZo1/jqdGbR7aefFy9yMvCH7PcxU6sfBOv/+pyDVbNa3XVDhZjT81l7La782jl6sqjLLQyf5vTjjxkfNenDuSyUpmmX3mSSFCvt+rnKjv4/hrdMjH/DvKZL9L/w9I58AAgAAAAAAiDk2gAAAAAAAAGKODSAAAAAAAICYYwMIAAAAAAAg5tgAAgAAAAAAiDk2gAAAAAAAAGKODSAAAAAAAICYS+XyYKN72twxpXsbzXrZvZvdjHRvn1kP+XluRmZuvVmP1q53M1K1NWZ9tKnazQjRLHdMZv02+zxadrkZibIy+zx6B9yM0e0tZv2Cja1uRq50zy1yx/Q1BLO+5It73YzMtBKzHsrL3YxdfzPbrNd/8T43Y+QvTzTrmZT9WCVppMTfLy6//TGzXrRm0M3wenHfqgo3o/pa+zk5+4luNyOn0pE7ZM+Z9ry16Ns9bkbycK89oGqGm9F1+myzXnLzg27G6MtPMOtR34iboYTfs2HtRrOe2rHTzUjOmG7WB0r9ZTT8YYtZ3/zf9vWZS8PlSXfMrlfbc8H8r2bcjNSBg2Y9c/xiN6P1JdPMeu1X/Llx8JyTzHpet9+LUWocf5f22Cb7OOPpxcpKs77/BHvulKSqb95v1rf8+yluRs6M4xpvOc/ugQXX97sZeW0dZj1zzEI3o/0Ee12a/h37eZekwVfZvVhwyF8/kwN+v6b37TfrqdY9bkaixL636Vrir9NlP3rArO/69Co3I5fyO4bdMW0vKTXr839ovz+RpLw9h816tGCum9G9vMqsF9/ysJsx8tIVZj2vw+/HMDSOfnTWgnH1o3PfeHi5f69d8T37Gm39+NTpx4KD/nuytpfb68Xs2/y5MX+r8z6n2X7PLkndJ9SZ9fH04ujpx5r1vIPOva2kRJd/7aUPd5r1sL/dP47Ti92L7DVLkkpvsufG1o89/17kE0AAAAAAAAAxxwYQAAAAAABAzLEBBAAAAAAAEHNsAAEAAAAAAMQcG0AAAAAAAAAxxwYQAAAAAABAzLEBBAAAAAAAEHNsAAEAAAAAAMRcKpcHS5aXu2OKb3nIrIeaajcj6uiw6yPDbsbWt5aZ9YXrC92M7lWzzXrJjl43IzE86o5J9/eb9VBQ4GZEAwNmvWtljZtRtq3FrN9w0bluxjt+7w6ZEBWb+9wxRYfs521god+L6Xx7j7W0237tJGnweHtMqtZ/bbadbV/qZdv9veCigxl3TGZw0KwnCv3rJuTnmfW+M/3XLnF9iVn/2adOcTMuu9kdMmHyDvhzwdyfDJn1dEm+m9F1aq1Zr/zlFjej7WV2fclDs9yMXS+1+yDV5/dJ9SP28yFJKWeuTxy72M2Itu4y6y1/5V87i++z15Pmm4OboQv9IRNh2vpOd0zITHvex2k9z+7F+t90uRl9DfaclJrT7GZsPStpZ/T6t0nVj/hzY3LUXsvD8cvcDO3aa5bL39Tmn8ePK816492Rfx7v8YdMhMSw/7w2/speHxPDaTdjz2sbzHr9z/e5GQPV9jU8nnW65XSv10rdjPrVI+6Y/HV2L45nXtSOPWZ5/7n+/Fxxr30P1fhrf63X5f6QiRKl/Lm+crP93Cb7/dfn8Ol2P5Zv9+8bOxba81pZpT+H7z7dXocTo/46PXPdOPpx41aznly2yM2IWlrNevvL/fOo+rW9JtU87L93zJXhGUXumJnr7PvxVK//eDrPnG3Wyzf467Tbi9Mr3Iy2U+zHGzL+81H9qP18SFJyp91HYeU41un128xy21/4a9LS/7HXi5mP+f3s4RNAAAAAAAAAMccGEAAAAAAAQMyxAQQAAAAAABBzbAABAAAAAADEHBtAAAAAAAAAMccGEAAAAAAAQMyxAQQAAAAAABBzqVweLDM05I5JFBeb9dH97X7GiiVmfaSyyM1YfHWrWd/2sRPcjLKWyKyXbtjmZqiwwB2Seenxdj3p7/NFqWDWy368xj+PM44z6wdX+M97roRHN7lj8k5eatefaHEztl262KyPvrLOzVh0+QGzvuNd89yM/MN2vXZ1h5sR+v3rd/c/rjLrST9CM9bbg+a+7TE3Y+As+5o4vCTpn0gOHTh9pjum6iH7NUpt2+tmDKycb9Z737nIzVj8b/Zx9ryuyc0o2m/PjXV37HYzouFhd0zn+aea9b46f26saCo360s+7c/j6WVzzPpo8dT5u5iuZRXumPzutFlPHex1M3qb7PVg80Wlbsbir9lz455zG9yMsh12ve43zuQpKUR2P0tS+0WnmfXeZjdCdX+wn7Oi87e7GekFs8x6NHVaUSOl/i1qJs++dylft8/NSBeWmfVdb6h1M5pvajPrB141180osSNUe49//xtG7WtTknpfe7JZP7DCf96bfmGPWfTBnW5GZq59fUZ5U6gZpXH9lXliyJ4LEt39bkZfrT0HD5eWuBnN399l1g+9aqGbkedM47Nu3eNmKNjXpyQNvsJ+P7V7lf8+qOnneWZ9yT85E72k4WX2vUuU8B9LrvQ25LtjyncOmvVER4+bMTBjmlkfPaHSzWi+0X4/3fly+75UkvJ77Ouq9g5/vlHCv4BHTjvGrLetsvcoJKk+z762lnyyxc0YnWOvOfldI26GZ4rNrgAAAAAAAJhobAABAAAAAADEHBtAAAAAAAAAMccGEAAAAAAAQMyxAQQAAAAAABBzbAABAAAAAADEHBtAAAAAAAAAMccGEAAAAAAAQMylcnmwsGCOOyZdVmDWkz1DbsbOcyvN+pzrd7oZo617zHpJW6ObUbF90KyHoiI3Y/Ckee6Y5EDarB9eZj+nklR97X1mff/7V7kZDXfYz1n16l1uhr72IX/MBOh80/HumIEqe3+0Kn+um1G58oBZL/3XcjdDIZjlv3nzb9yI6371MvsQ/f51NTB3ujtm+sZRs753VdLNqL9ui1nf/cGT3YwZ60fM+qzP3+9m6Mrc9KIkVWwecMe0n27PazMe96/z7pX269xwm78khAE7Y/6bN7sZrf8536xHpf7cGCVL3TFlLf1mfaSoxM0ouX+rWd/6j4vcjLk/6raP8ZMH3Yxcye+21xNJ2nea3ScNQxVuRvWCg2Y986OZbkaUn2fW3/OeW9yMa775OnfMRKh6rMceEMrcjKKHtpn1bZctdjNm39prH+O2NW5GrhR0DLtj2lcWm/WifX4v9i2379Wav+//XWmUtMcs+4cn3Iwnr1lu1jPl/ryY6PPX8sh5OJWb/Dkgsdm+n9v2T8vcjLk3dpj1/N3tbkYupbr85/bgMvs1yu/2+7FnkX3/suB6/7rwlFzY5o5J/Fe9WU9X+Gtwos++tiRpuNxeT2rW2M+HJIUNO8z61k8d62bM+2GnWc/f2uVm5MqMNfb6KUntp1fZGUP2PaUkdS7LmPV5N42jFwft62bkHYfdiLJ/t6+bTKX/XirRZa99kpQusN+j1D7g36sn/miv0y2XrnAzZv/0kD2g3X/OPHwCCAAAAAAAIObYAAIAAAAAAIg5NoAAAAAAAABijg0gAAAAAACAmGMDCAAAAAAAIObYAAIAAAAAAIg5NoAAAAAAAABiLpXLgx04rdIdU/WdNfaApfPdjKarHjLrUcU0N8NT/UCnOyZzdY9ZT5/V7WYkRjL+mNXrzHr1ajfCVbu6yx80OGSWQzL5/E9kgvTX+Hufs67baNajxlo3I3XuDrOeOGahm5HevM2s33TdK9yM5nNa7QGHe92Mmuv8nu84o8Osz9uxyM1QIpjlGU+OuBHpIuf1DVNr73ugtsAdU3vrdrMezahwMxZcuNmsp5pmuRmje9rM+tpNJ7oZxU3281/50z1uxsZ/W+aOWfzBJ8169R5/TcoM2/0292b/2umbU2rWS7eWuRm5Mlzuz9Nzb2i3ByT96yv1GnteS832r/PRHTvN+ucfeLWbUVxo10PrXjfjmN/66+Pjpxeb9ZnDTW6G0mmz3PTLQTfi8DK7F6vW2+eZSyNlee6Yut8cNuthaNjNWPC39jqdqql2M0b37Tfr9z5+kpsxI9+uhyftNUCSNnxtqTtm0XsfsweM4z47Graf1+Y7+92MgUZ73iva2uJm5NJAQ4k7pu53h8x66BtwMxZ9wO6lRJl9DUtSust+/7HnvpVuRmG1fS9WcbdzXylpw+f9e77FH/6jPWBBs5vhzY1zbulzIwbr7Oe1uMd/7XJlqK7cHVN9n9OLg/7cuPBS+31QotS/JtI9di92r53rZiQrIrNetHoc94yf8e8ZF37cfj8dGuvdjMzoqFlvvtVesySpv8l+fUt6/fnVM7XeBQEAAAAAAGDCsQEEAAAAAAAQc2wAAQAAAAAAxBwbQAAAAAAAADHHBhAAAAAAAEDMsQEEAAAAAAAQc2wAAQAAAAAAxBwbQAAAAAAAADGXyuXBqlcfdMf0nnuCWS9sH3LHShq3AAARwklEQVQzQjpt1tMHD7kZqVkNZj1q8x+L/uKAnXHaCjci+dtH3DEHLz7NrM/87zVuRuQ9ZyV5bkbo7bOPMTrqZuRKGMepdNxQadbzry11M0r3zzTro49tcDMyZx5v1mddv9HNSF992Kz3/PUp/nm87FF3zEWbtpv1L195qpsRjqsw64eXBTdj/g32491zif94cynVl3HHbL94nllvurvXP05DvT1g1J4HJCm5aL5ZX/yhTW5GNDBg1ntfu9LNWHjxw+6YLTccY9Yr7ilyM5RoNMvROP4apea37Wa985xlfkiODMzwH9C+T04z63Ou96/RwsEm50QG3YzkskVmfcml9nwkSZmeHrPe+cYT3Yx1K/01duVa+/r86W3T3YzkoD/GM+se+/Hu+oB/X5IrQxVJd0zLX5Wb9YXfsecaaTzzon/D4M+LT7oZGafnu958kpux8O/9Xhz8hT2n9X/ffk4laeR0+15d/pKmmevse8bO1x/nh+RQ8JdHbXi/PTfOu7HEzShI209e1N/vZiQWzDbrc774hJuR6bXnrMN/499HLXzPg+6Y1p8uMeslN/v9qOV2r0QJf02q2GL3Y9fxNf555EhyyG/GHW+sMuuNv7IfryTlOe8No35/nU7MtuebOVc97mZ4c2P3G/25cf6H/V7ceK2dU/s//v1RdEq1WU8OuxEq22Kv073H1vkhDj4BBAAAAAAAEHNsAAEAAAAAAMQcG0AAAAAAAAAxxwYQAAAAAABAzLEBBAAAAAAAEHNsAAEAAAAAAMQcG0AAAAAAAAAxxwYQAAAAAABAzKVyerSRUXdI8R2PmPVo1M8Ieflm/cCFK92M2rt22cdIJd2M9vesMut1P9roZqRDcMdUPdpr1hPzZrsZ0c5Ws57a0e5mjPb02BmzGtyMXCnfnXbHFL+mxawnp3f6B0rZl1jvL+a6EdM+3G/WQ3mZm9F68WKz3vyzA25GemTYHfPtC84z69Py7MciSakndpj16Y/UuhnpJzeb9YZooZuhL/tDJkom37/Om66436wniovdjMgZs+O9C9yMud/aada7/3Kpm9HTaM+ftffZc4kkKeNfw3OvseupzsP+cfYftOszKt2I9OZtZr0iL7dLsSW/N3LHLPjbR836eHpRlRVmecNV/nqx5CN7zHr3y/3rvGu23Ys1awbcjPH04pr3n2DW5x52+kxS6LPPJVPprwWZdU+a9eYefw7Q5/whE2G00J8XF777IbOeKCx0M6Iy+3nb/NF5/nlcucmsH3jLsf55OLeV1Q92uRmZcfRi6vPTzfrMljY3Q4NDZjkq9eeA9FZnrd/b5J9HDg2X+/f9C9/9oFkP+fb7E8lfpzde4c9riz+xwawffONyNyNk7HrlBvu9hyQp8teTui/Zz0nezt3+YUZG7HrtDDcj87j9nqzkJP85y5WB6gJ3TNOVdi8m8vPcjGhauVlvudhfL5q/8phZP3C+PzcmnbcflRv9XozG0YsLvmvPa6nte92M4Lxvj2bY9z6SlN6w1awXFixzMzx8AggAAAAAACDm2AACAAAAAACIOTaAAAAAAAAAYo4NIAAAAAAAgJhjAwgAAAAAACDm2AACAAAAAACIOTaAAAAAAAAAYi6Vy4NlKkvdMfvPPtms19+x280Y3dVq1qu//7if0ddn1tsuW+Vm1H/pPrPed679WCWpaP+AO0aPbDDLmeMWuxGJ0hKznq6udDNC+0F7QH6em5ErQ2X+3mfrN04w6xWP+4+n/rZdZn3aWzrcjHRnp1nf/eNlbkbjG+1e3Pkxv59r68rdMQXr7euz/a/n+cfZkDTrncdOdzMq9tr9uv+MGW5GLiVGI3dM22WnmfW8Hj9jxhP2fDLn+/vcjNHWPWZ93yVNbsa8jzxoZ3zgFDejNnGsOyZvr33t7Durzs2o/kGbWR+Y68+NBdOOMestZ5W5GbmS35Nxx+y7xO7FgWq/F6set8cs/sIhN2PUWXPaXl/vZsx/2zqzvutT9mOVpFmJ490xeXu7zXrLm2rcjOavPmbWu09pcDNKC+3rZsM7Ct2MXClvGXLHHLrIfn3664KbUbHF7vlFX7fnAEkaddbpw8f619WCSx4y69uvONXNmJNa7o4paLGvrT3n+n1Ud90fzfrQMj8jNdOe97a8ttjNyKXSFvt9geTPjakBf24s2Z8260uuHsc63dNj1g8f65/H/EvtdXr7F/x+nD+81B0TDvaa9YOv8O8ppv/Enhv7T57tZuRNt+fx9uOnztxY0trvjtn3Xvs+Kn8c94xFh+xenH3Tfjcj3W+fa98sf45uuuJ+s77zn/11ek7fQneMDtjr9KGz/fcw02961KwPrmh0MxI1x5n1/ScXuBnuMZ53AgAAAAAAAKY0NoAAAAAAAABijg0gAAAAAACAmGMDCAAAAAAAIObYAAIAAAAAAIg5NoAAAAAAAABijg0gAAAAAACAmGMDCAAAAAAAIOZSuTxYYssud0zdFrueGRzyDxRFz68uKVFcbNbrv3Sfm3HootPMes2d292MTE+vOybMm23WR/OTboa6euzzWDjLP4+RYbM+OHuGfx45MuOnT7hjpj/eZNYPnljuZqT37jPrySb/efVevaa3bHYz9n1glVmv/32/m5H3xA53TDSrzqx3L/Cvvep++1z6av1967KODrM+523ORJNjeV0j7pimmw+Y9fFcX4n7/mjWQ4P9+klSsso+Tu0DGTdj+C9PMOuFh8YxR6/3+3HoxAVmPZ0f3Axl7Mdz4Pg8N6Lxi4/Z53HeSv88cqR4jz8XlK23x/Qsr3IzSm5/1KyHmpluRnJes1lv/IF/izNw3klmPa/PjVDqka3umNFj5pr1yG8jJSqmmfVDy8YxN/5so13/6Dz/RHJkpMx//apX2/PicL2/Tid/Z1+f0fQKP8O5D2v8lT+nRatWmPWCTn++Cpt2+sdp9Od59ziFhWb9wAkFbkb9l9bZxzjn5D/rnF5oo2X57piGO+17vqHGSjcjda/9vGgcc2Oqod6sz73Ffy+VWLHErJdvcyOkzS3ukPRye86JxvFRhVBg91t38zjmkmvXmvXRM07xTyRHhiv966vhtt1mfbTO70U9tN4sh2p/rU81N5r1mof9+9/kAnv9LGx3I6S99lohScPHzTHreX3+/W0otF+bznn+PFL9jfvNesGCU90MD58AAgAAAAAAiDk2gAAAAAAAAGKODSAAAAAAAICYYwMIAAAAAAAg5tgAAgAAAAAAiDk2gAAAAAAAAGKODSAAAAAAAICYS+XyYJm+AXfM4F+usAdE/nGK2vrMeuj1zyNq3esfyFF8MG3WM909bkamv98dc+iMmWa9+tbN/nGcerjvMTcjWVNt1lOb97kZuZIoKXbHdM8pNeulraP+cRbONeuDdWVuRv6+drMejQy7GZWbR8x625n+8zFrdZc7Zvf7lpn1hf+5383IpO3rpuF7G92MoVesNOsd/+xGSL8ex5gJkt962B0zWlth1vN6/D4ISxeY9ZFphW5G8lF7Pim9da2bEZ241KzveYm/NFV8z58/O+cVmPWGn7a4Gelh+9ppuqvTzWi/0O7HeT845Gbo4/6QiZBq96/z0eppZr241V+3EnObzPpQfbmbkfegPRcUbNvpZoQVi8367nP9uTHT4/fi/pNLzPqcmw66Gel2e0zjb2rcjNZLTzTrtV8ddDN0nj9kIpQ8sMMdk2m2H3N+u30/KEmRNy9W+PNi6mG7Fwu373Izwkp7Xuydba+N0vh6sXe5vU433LHHzUh3dJj12gf9++xDF51s1uv+4N9j5VLhRv99QabKnhsLdvlrvZy5caTGPoYkpf643awn/qfNzUivst+P9dcGN2M872G6Fthz48x7x9GPznFqHvSvi67zTzLrSb+lc6Zovf/6RSVFZj21z793UUOdWR5tmO5GJDftNusFd9l1SRo97VizPljlRrhzliQNzlho1qc97M8B6QF7Da150L/HOnjRqWY9NQG9yCeAAAAAAAAAYo4NIAAAAAAAgJhjAwgAAAAAACDm2AACAAAAAACIOTaAAAAAAAAAYo4NIAAAAAAAgJhjAwgAAAAAACDm2AACAAAAAACIudRkn8DTFd79qFkPRUVuRjQ4ZNYzI8N/1jk9k9ScZndM0a0PmfWBc05yM+791n+5Y15zxmyznp5T72YkugfsjE1b3QxVVZrlAydO9zNyJCorcccU3/KwWU+/ZIWbkSnKM+upe9a6GYnGWXZ95gw3I3nfJrM+M7nIzbh252p3zHvfeIxZz5QVuhlh2QKznn5sg5uRGLGvz53vybgZOTU0jjnpwT+a5bBiiRsR5SXNet6ug35GiX3tJGb413lm3Waz3jBtuZux44f+9Tf/0/vt86gsdzOSefYyObruSTejpn+eWd/6zmo3I1cy5cX+oDVP2BlnHOcfp7bMrBdsbffPw5n7EsMjfkZ7h1mefbP/fGy55hR3zMLvdJv1KOH/fVxyVp2d8Tv7/kmSZvUuM+ubLylwM3Jm+jR3SPSIvR5Ex/prW6bQvsbz9nW5GaHCPteQ9tecsNvu+Xk3+fdy+9+/yh1Tf489z2dK/Ptsb54fTy/O7LTXrM3v8F//nHLWAknKPL7RrCcXz3czoqSzTu884Gfk2/eeyYoKN0Mbd5nlRjW5EW2X+f3YeJuzTpf6c3Ci3F7L02vs+ydJmhbZ9x2Hlttr1lST3rLdrCfnzXYzMpX2Y07t9NfpKLLnvuQ47hn1xA6z3FDgX1cH3n2aO6b2XmduHMf9UaLLHpNeu97NqB5YaNZ3v6bKzfDwCSAAAAAAAICYYwMIAAAAAAAg5tgAAgAAAAAAiDk2gAAAAAAAAGKODSAAAAAAAICYYwMIAAAAAAAg5tgAAgAAAAAAiLlULg+255IT3TGNt+w1673X+Mcpe+eQWe85aZab0dVsPzUNv2h3M1Jzms16f6G//3Z2/XHumG1fqjXr827qczNC34BdP36Zm6GWNrNcef0mP+M7/pCJsPWzpe6Yxv+yn/szrn7AzbjvfSeb9dZPr3Izpq/aZ9aLrqpwMwpa7F7bd3Kem/G+pWe7Y6LbOsx65oqZbkZ/TYFZTy8/1c0o2zlo1pu+mXQz9P/8IRNlyyVz3DFzfzzDrP/89u+7Ga9+1flmvevkBjejfaXdS3X3pd2M4hb7+mtfme9mzH374+6YLdcvNesLrux3M/oXVZv1vPpKN0Nddj8WHAp+Ro5s/FCJO2b+t+258Vc/8ifys1//drN+8OWNbkb7maNmvflnboSKWnvMetuZ/m3Soo8+4Y7p+0mVWS/9kD8H731VvVkvb7F7VZKSQxmzHhJ2PZe2XuivF/N+YL8+P7/rB27GOWfZk/3B0+17LEnqmW1fww2/s+cASUqM2M/9vlOL3IxZ1z7mjtn4jUVmffFnO92MjlfMNetlO+vcDPWPmOUoP/IzcmjbO/31cc5NxWb9rl/e6Gac8xdvMut7Xm+/t5CkwSr7uWv8pX3PL0lK2j3dtsrvx6avPOKO2fztxWZ90Sfs+0pJ6j7D7sfS7fb8K0lhwO7HhL3c5NTOt812xzT91H597rr3ZjfjNWe8zqwffKV/79pfY/dRzdpxzI3D9tx4cHmhm1H7zbXumA3XHGPWl15u71FIUv/J88x60Q6/nz2ZCdi94RNAAAAAAAAAMccGEAAAAAAAQMyxAQQAAAAAABBzbAABAAAAAADEHBtAAAAAAAAAMccGEAAAAAAAQMyxAQQAAAAAABBzbAABAAAAAADEXIiiaLLPAQAAAAAAAC8gPgEEAAAAAAAQc2wAAQAAAAAAxBwbQAAAAAAAADHHBhAAAAAAAEDMsQEEAAAAAAAQc2wAAQAAAAAAxBwbQAAAAAAAADHHBhAAAAAAAEDMsQEEAAAAAAAQc2wAAQAAAAAAxBwbQAAAAAAAADHHBhAAAAAAAEDMsQEEAAAAAAAQc2wAAQAAAAAAxBwbQAAAAAAAADHHBhAAAAAAAEDMsQEEAAAAAAAQc2wAAQAAAAAAxBwbQAAAAAAAADHHBhAAAAAAAEDMsQEEAAAAAAAQc2wAAQAAAAAAxBwbQAAAAAAAADH3/wHgVjBgdAqwTQAAAABJRU5ErkJggg==\n",
279 | "text/plain": [
280 | ""
281 | ]
282 | },
283 | "metadata": {
284 | "needs_background": "light"
285 | },
286 | "output_type": "display_data"
287 | }
288 | ],
289 | "source": [
290 | "f, axarr = plt.subplots(1, 7, figsize=(20, 7))\n",
291 | "\n",
292 | "r = torch.zeros(128, 256, 1, 1)\n",
293 | "\n",
294 | "for i, ax in enumerate(axarr.flat):\n",
295 | " phi = model.representation(x_c[:, i], v_c[:, i])\n",
296 | " r += phi\n",
297 | " ax.imshow(r[scene_id].data.view(16, 16))\n",
298 | " ax.axis(\"off\")\n",
299 | " ax.set_title(\"#Context points: {}\".format(i+1))"
300 | ]
301 | },
302 | {
303 | "cell_type": "markdown",
304 | "metadata": {},
305 | "source": [
306 | "## Sample from the prior.\n",
307 | "\n",
308 | "Because we use a conditional prior density $\\pi(z|y)$ that is parametrised by a neural network, we should be able to continuously refine it during training such that if $y = (v, r)$ we can generate a sample from the data distrbution by sampling $z \\sim \\pi(z|v,r)$ and sending it through the generative model $g_{\\theta}(x|z, y)$.\n",
309 | "\n",
310 | "This means that we can give a number of context points along with a query viewpoint and generate a new image."
311 | ]
312 | },
313 | {
314 | "cell_type": "code",
315 | "execution_count": 189,
316 | "metadata": {},
317 | "outputs": [
318 | {
319 | "data": {
320 | "image/png": "iVBORw0KGgoAAAANSUhEUgAABH4AAACmCAYAAACsl0hIAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzt3XmwpFl6HvTnfFtm3rVuLV29TvfM9HRrpmf1aJCskTSDPIqRBcgiBEYegbBBhiBCEAF2WNjYZjBjbCtAGAth5ECyzCgCS2Bsh2wLCGGGsCRLsyhGQrN0T6/VS1V1rXfL5dsOf7zP+92lu7qrq2oq8373+UV0ZN+beb/Me/Otc06e8573hBgjRERERERERESkf5J5vwAREREREREREfnm0MSPiIiIiIiIiEhPaeJHRERERERERKSnNPEjIiIiIiIiItJTmvgREREREREREekpTfyIiIiIiIiIiPSUJn4WUAjhKyGEj8/7dcjRo9iRW6G4kVul2JFbobiRW6XYkVuhuJFb1afYWbiJnxDCp0IIXwwh7IQQzocQfjWE8J134Lq/EEL4zB16jX88hPDrd+JaryfG+ESM8XM3+VqeDyF84k48bwjhZAjh74cQdkMIL4QQPnUnrnu3KHbmGjs/zr/9LITwC3fimneL4mY+cRNCGIQQfo5tzXYI4cshhD98u9e9mxQ7c21zfpF/860QwlMhhB+7E9e9GxQ384ubfdd8VwhhGkL4xTt53W82xc5c25zPMWZ2+N+Td+K6d4PiZr5tTgjhh0MIX+Pnq2dCCN91p679zabYmWubs3PovyaE8NO3c82FmvgJIfwnAP46gP8KwFkAbwPwPwD4I/N8XcfIzwAoYX/7HwHwN0MIT8z3Jd0cxc7cvQLgMwB+ft4v5K1Q3MxVBuBFAB8DsA7gzwP45RDCI3N8TTdNsTN3fwXAIzHGNQA/AOAzIYQPz/k1vSnFzcL4GQBfmPeLeCsUOwvhx2OMK/zv8Xm/mJuhuJmvEML3AvhrAP4EgFUA3w3g2bm+qJuk2JmvfW3NCoB7AUwA/K+3e9GF+A828N8B8K+/wWMGsAB8hf/9dQAD3vdxAC8B+FMAXgVwHsCf4H3/HoAKNqmxA+BX+P37Afw9AJcAPAfgP9r3XP8EwH+z7+u/C/tQ+24AUwANr3X9Bq/1c7CB6ecBbAH4hwBO7rv/BwB8BcB1Pvbd++57HsAn+P+fBvDLAP5nANv8mW/lfZ8F0MICYQfAnwEwBPCLAK7w2l8AcPYm/v7L/Ps8tu97nwXwV+cdG4qdxY6dQ6/9MwB+Yd4xobg5WnGz73X8HoAfmndsKHaOVuwAeJx/wz8679hQ3Cx+3AD4YT7fpwH84rzjQrFzNGKHr+PH5h0LipsjFze/CeDfnXcsKHaOXuwcev3/NmzCMNzW+zrvwNr3C30fgBpA9gaP+UsAfgvAPQDO8B/Tf7kvwGo+Jgfw/QDGADZ4/y8A+My+ayUAvgTgLwIoALyDf9BP8v57GajfA8t+eRbAKu/74wB+/U1+n88BeBnAe2GTKn8PHGAAeAzALoDv5Wv9MwCeBlDcIMCm/H1SBu1vvV4w8ut/H8CvAFji4z8MYI33/acA/tENXu+HAIwPfe9Pg/8YF/k/xc58Y+fQaz9KEz+KmwWJGz72LJ/3W+YdG4qdoxE7sJXHMYAI4HcArMw7NhQ3ix03ANYAPAXgQRytiR/Fzvxj53OwD6SXAfwGgI/POy4UN4sdN3xsycc8DZsI+e8BjOYdG4qdxY6d13n9/xTAp2/7fZ13YO37hX4EwIU3ecwzAL5/39efBPD8vgCb7A9QBsi33yDAvg3AuUPX/7MA/va+r38IthXhMoDv3Pf9mw2wv7rv6/fA/vGnAP4CgF8+FOwvg53I6wTYrx26zuQNAuzfgf3De/9b/Pt/1+G/P4A/CeBz844Nxc5ix86h136UJn4UN4sTNzmAXwPws/OOC8XOkYudFMB3wrYK5vOODcXNYscNgP8OwE/se96jMvGj2Jl/7HwbbKvOALb6vg3gnfOODcXN4sYNLIMlAvgigPsAnIZNGv7leceGYmexY+fQa38YltH09tt9Xxepxs8VAKdDCNkbPOZ+AC/s+/oFfq+7Royx3vf1GMDKDa71MID7QwjX/T8Afw626ux+BRYQT8YYb6Vo1IuHXmsO+0d/4PeIMbZ87AM3uM6Fff8/BjB8g7/TZwH8nwD+bgjhlRDCT4YQ8pt4rTuwlbD91mAd26JT7Mw3do4qxc0CxE0IIeE1SgA/frM/N2eKnQWIHb6ehr/vgwD+g7fys3OguJlj3IQQPgjgEwD+2zd77AJS7My5zYkx/naMcTvGOIsx/h3YB/jvv5mfnSPFzXzjZsLbn44xno8xXgbwU1j8uAEUO/OOnf3+LdjE1nNv8edeY5Emfv45gBmAH3yDx7wCCwz3Nn7vZsRDX78I4LkY44l9/63GGPf/Y/zLAL4G4L4Qwh97g2vdyEOHXmsFm6U88HuEEAIf+/JNXne/A68lxljFGP+LGON7AHwHgH8ZwI/exHWeApCFEN6173sfgO1dXHSKnfnGzlGluJlz3PB1/BysY/+hGGN1C69nHhQ7i9fmZADeeYs/e7cobuYbNx8H8AiAcyGEC7Dt7D8UQvidW3hNd5tiZ/HanAgg3OLP3i2KmznGTYzxGmx71/7r3ezvOW+KncVpc34UwN+5hdfyGgsz8RNj3ITt6/uZEMIPhhCWQgh5COEPhxB+kg/7XwD8+RDCmRDCaT7+Zo/ivAjbL+g+D2A7hPATIYRRCCENIbw3hPARAAghfDesAvuPwlI6fzqE8MC+az0YQije5Dn/zRDCe0IIS7A9jv9bjLGBFYX6l0IIf4izfn8K9o/rN2/yd7nh7xVC+BdDCO8LIaSw4lUVrNDUG4ox7gL43wH8pRDCcgjho7Cq7Z+9hdd0Vyl25hs7/NkshDCEzcSnIYQ3mv1eCIqb+ccNgL8JK8z3r8QYJ2/24EWh2Jlv7IQQ7gl2PO4K/xafBPDHAPzft/Ca7hrFzdzbnL8Fmxz8IP/7HwH8Y9j2hIWm2Jl7m3MihPBJH9uEEH4EdjrT/3ELr+muUdzMvc0BgL8N4D9kv7UB4D8G8I9u4TXdVYqdhYgdhBC+A5Z5dHunebl4m3vF7vR/sD2FX4QVWboA65S/g/cNAfwNWGXw8/z/YdzbS/jSoWs9j709ee8C8GVYRe1/wO/dDwvaCwCuwQpUfQK2xel5AD+871p/DcD/BZvdL/i6rgK4fIPf43M4WD38VwCc3nf/vwrgqwA2Afy/AJ64wev+NPbtQYetVkVwzyRscuYcf68/DRv8Psm/30X+jfyxfw7Ar77B3/4kgH/Anz0H4FPzjgfFzpGJnU/z2vv/+/S8Y0Jxs7hxA1tdibAieTv7/vuReceEYmfhY+cMX8d1vt7/D8CfnHc8KG4WO25e5/UfeN6j8J9iZ65tzhdg5Q+u82/xvfOOB8XNYscN789hBxFc59+k+/sehf8UO/PtrwD8LIDP3qn3M/CicoeFED4HC4z/ad6vRY4WxY7cCsWN3CrFjtwKxY3cKsWO3ArFjdwqxY5ZmK1eIiIiIiIiIiJyZ2niR0RERERERESkp7TVS0RERERERESkp5TxIyIiIiIiIiLSU5r4ERERERERERHpqexuPlkIQfvKeirGGL5Z11bc9Nc3M24AxU6fqc2RW6E2R26V2hy5FWpz5FapzZFb8UZxo4wfEREREREREZGe0sSPiIiIiIiIiEhPaeJHRERERERERKSnNPEjIiIiIiIiItJTmvgREREREREREekpTfyIiIiIiIiIiPSUJn5ERERERERERHpKEz8iIiIiIiIiIj2liR8RERERERERkZ7SxI+IiIiIiIiISE9p4kdEREREREREpKc08SMiIiIiIiIi0lOa+BERERERERER6SlN/IiIiIiIiIiI9JQmfkREREREREREekoTPyIiIiIiIiIiPaWJHxERERERERGRntLEj4iIiIiIiIhIT2niR0RERERERESkpzTxIyIiIiIiIiLSU5r4ERERERERERHpKU38iIiIiIiIiIj0lCZ+RERERERERER6ShM/IiIiIiIiIiI9pYkfEREREREREZGe0sSPiIiIiIiIiEhPaeJHRERERERERKSnNPEjIiIiIiIiItJTmvgREREREREREekpTfyIiIiIiIiIiPSUJn5ERERERERERHpKEz8iIiIiIiIiIj2liR8RERERERERkZ7SxI+IiIiIiIiISE9p4kdEREREREREpKc08SMiIiIiIiIi0lOa+BERERERERER6SlN/IiIiIiIiIiI9JQmfkREREREREREekoTPyIiIiIiIiIiPZXN+wWIiAiQIPD/AiIiAHS3IjeSMm6i4kbeIrU58lZ4vCyFAQDgRLqKIuQAgK12BgAYxykAYNaWAIAWDYDDcaUYO248dkaMlzRkXRRMYwUAaGILAGjR8h7FyXHnPVTO6YoQEsRocVEfalvUd90cZfyIiIiIiIiIiPSUMn5ui89FapbxuAuMhSykAIBBVqBsbBWjamsAe7PRoZtvfb1Z6nDg5jWhFXhHbCFHWxYsDgaMmTPZEgBgKVvD5WoLAHCtHgMAmmgrG4E/061wxL0A6f6vi52DwRMSe57YNod/Qo4Qj5flxLrv+xk3y9lJnC+vAwAu1tsAgJpx4zHRxreyMsbHMOb24klxc1RlONjm3JMOAQDr2T24XFubc6mx2zpav+V9TmSfsxc74c3jqIsdreAfZcuJZWm8PT8BAPj4+nsAAN/32A8izy3759lXzwMAfufqkwCAJ0vru16avQQAuFJdBABUcYZJtc0rez92KD7YV0F91ZHlw5C1tAAAPFqsAwC+e+MRAMC33Pft2J7sAAB+/VXGzPgVAMBlZovtsE0qG8sma9Eiep/2ps+smDnKhsHGNz4u/vDoAQDAh9Y/jGulxc1vbz8NAHixugwAmMD6rN3G2p4qWhxFRLRvGjfHhzJ+RERERERERER6KsR492ZFQwhHYArWZosDV7lCFrpV9RDDwYcmNm/W1lwZu4t/y0UT4+E/zp2ziHGTcM604MrUqWwFAPAdpx4DAJxdT9E09rKv1na7zdj62uXnAAA7XNWoU66ojnJMatsf3xZ8ontsRTZ5u62WtF/bBAA0F23Gu92xlRDUNY7iCsc3M26AxYydQbA393RqKxnvy+8BAHz3+jsAAB84dQp5anE1ZlbHVm7x9tULvw0AuBxs9eLqkl1r6+QqfuvVawCAmSWaIS6dBgCEsxaTyWVbca0vvmD379jXsdxG5AoJcHQyyY5bm7OSjgAAj2S26v7t+X0AgD+4+nYAwPvufRtyxtZuY/FzNbVf48vnfhUA8Hy09uJcbt+/tFTg6zsWN3XLdqiw62PNVtiS7QsAgPbaq3b/zFZhYzsDuKJ2lBzHNmfIuDiTWj/13szanI8uWZvzkRPvQMGV+TFrcGwW1uZcPP95uw0TAMBLQ/vzXVwb4TfOWzZH6UOgxPopDBg7sH6q2XrR7mfWR2x2AXjsLNyf64aOXZuT2PjjoXQDAPBE9ggA4P2jxwEAP3Df92FpZO1FHFhszdYtjoa7ltWzmVoMvHSS8fP2FD/15D8DAFye7AIAqqH9TNw4CQAIX30GAFC/8BQAoN1+2e4vtxHbCV/dwv25bug4tTme/b7O8c0jqcXH+/OzAIAPLT8CAPjkox/DYLQGAKgH9tjdZY53XvxNAMDFxsa7T+fWbz2znuOXvvTPAQDTGbOAWs+St8yz4JmJE8sCiY3Fn/VVR2d8445dm8NxzsNscz6cvw0A8JHRuwAAn3jwoxgMra1pM2ufJkvWVzWXfhcAcDVeBQA8M7D3/utrLX7m8/8PAKAsrf3wzHf/2N7liVW7/j/8ztGLGeCN4+bYbvXyiR1PY+4menIbMOer1ogkawmSzL6XpPbnyjhAml63hqe6ZoHSTJhW1rb7Ulff8ivDUerQjh+LkwE/kN/DNMTHl2wg/W1nHwYAfOv7H0daWKO0y39mm629r69sXQIAXElskufKijVA19cSXPigxdr1ey3Gmvs5EFqxzrN8yT6E7fBD/u5XLL169hvnsPtrX7aX2HqDJYvEJwvXE2tbHuUH+Cdye48fTFcBAI8/9ATyJev86qHdTgYWF//CH/wW+9pCC9c27EPa+ZUCa++y2Hs22vV3V+26WLLB1dJF6/B2r9okz+z8FQBA+ZXn8epnfwIAEJlaLYsjZdyc5oDo/bkNiN7L2/uCtUEP3vMOZLn9f53YY+8rrL16/2M26N5mm3Nh3T6pP7sS8Esfvh8A8GJm8TfZsMfGFbt+/nX70DU7z37uBYub6itP49o/+yl7kVFtziLyNueUTzJnNhn8wcze40cSayMeO/Me5MNlAEDD28mI25bf8QQAYDq08c2Vk9aPnTuVIj9j13thag3SztDatHbJBubFRYuZ2cvW9lTnrO+rnv0Grj35nwMAYvQP8rIoUnA7KScBzwaLiRPRxiU5/7nnDZDVFmNhYPcFWP8zYt8UC/vZe+63H4pvC/ieH/wxAMBXuefgChcwSl5j5VWLtdkrFj/1CzbpPPvyUzj/y3/WrtMtVsgi8f7qBCeb35bY+38W1kYsc5J4KR2gyKyfajkBlDEO7vno9wAAHgjWXz28Yj/02HrAq5/6NwAA35hyrJxY21ZxXDV8wSaLqhdt4rE9Z/1X+ezvYfvZn7MnV3+1cLzN8fHxQ4mNR85Ge39HbGdGcYQirvCHbKEhy62tWXni4wCAM7n1KWdXrR1520aNb/yRfw0A8OSUC/LcSla2bL++YAvy9cu2ONFe5OTz5SdRXv8iX+XRnAQ6TFu9RERERERERER66vhm/HCbVlLYnyDl6layYjOHw4dtlnr0nhMoTtisdMrVjwFXNLaet4yf3WdtFWv8tKUWtpMK9cRmqveKH/otZxe96OG+41TtJt0rhBi9KLAKIy4Kf7c2MhasG9qs9EOFxchqYo9YCevIMouhjIURPakyvf8MAOBEZrPRG8uW8fPqoER8wlY+0nWLj9mazWw3mcXcmUcfAgBM32kXqz5k15h84iK++iXbwlNfucRXqXhZRCe5ovEg0+jXor3XaWXvZVJHJFzdyJi941t4kmjtVMY6dUVpsVXMcpy4zzJ+1vnYdGTxV6f2mDNMyT/xNouL9H32+PIDj+HqP/xZAEB19ff4KvuxstEHfgzu2cTe1wd5u9rae5RVtrqVTmskjQUGk1OReT8HZmDwjhVuQ92IAfe+07YCjpkttL1sq2hNbvG5wdXY+H675qC0563OfSt++/M/b4+depsji8S3XdzLNufhYP3UOv95Z3XJWyDl9sCEbU7LOEvYf6VsdDhkwjAJ2HiPbRW7VnJvcm7XrzhWWrvXMori4/Y68vGjdu3n3o8v/eTfAgA0k2f4atVfLZo1vo8nYLcZ90U0DbeptzM0PMQi1BYftW9tbyzIJhwT7bBP26oCZuvWpgQGU8FMj8js+jVmKqZn7VpLT9i4p/7Ao7j4T/6GvYbNZ/kqFTeLxMfIJ5gVv8FMjoKHnIBtTluWaJk6Fituz+JDZjv2MyULh9cDtkl1grXH32nXBzPMhnZfyYL164/atRJmdgx2ecjK09+JL/1nf9+uM7t4R35XuXN8nOOZYie9zeGWrJbj42ZSo239MzLLrXCMO2vsGiXbj6q22GiSiJPfZVvGTrM/S5bsvik/i48etu2r2OVBKtzJU339JXzj5z9lT1dv3qHfdr6U8SMiIiIiIiIi0lPHMOOHtXxYUDdb5er4Guv3nLGvR4/ZCun6+x7EcM1WsTKugA1ZeTfhZtV0xWYOvc5lfXmC5jxXQNuDK+eB+wrzgnsUec0YOQuZrCKw6GFdWh2XprYCVZ75E31aXKvyc3OCGTjrnGnOuepUzizTa3K5QsqaCLvB3qdtFuy9ypns7cxicHPZ5l93lzJcuW7v7RUePVhyxR5Du36RWNZGSO37S6zfsvrACp7h6mvzmxY3sdE+5kXSHW/Kf/MF591rroSNeWTpdGfXF8VQlxYzU76V05dt3/pOYvFwZcWudWFthHOPWebHJcbblG0ayzKg4POCK7BDxmM+GCI7Y4Xzqmtfscfcco0yueMYOBtcqWJTgIYdzqyxNqfa3UWT2PtWZ4wBrnhNWJh5mzUTLq3aRS9tDPDKOVvFusrV1+lJxo0lAGG5ZcYHV8Yy1sFbOr2KbN0KTDfTy3yxWn1fRL6K6mcGlIydMeukTMfXkZXW5zCZA7PWxijjLWtzxsz4uXLN4uCV0wVefIe1OZcnzO4oLDYadltpwWzXmuMuDjmHp5aQr1hR8maizI3FY+/FmtdNYdvj9UJ9ZDFNKgQWjAf7r5Ltxe7U4mXCgwgu7VqMXN4NeO6iPfbSsj3PLFpcNAO7/vUxD89g4V6vVTVYHiHdsOyfZvO5A69VFssqs8UK1k9t+T7V/Nwya0vEkgWaWah5OrA4uH7OPvNMc7Y5zIC/MCnw/Hl77GV+hput2fO0rIM4Ys2WjG3QYJlZ+A+dQHrCspzbi6/yVSp2Foe3Of6Zyt63mp+FpqzLNG2maBk3MbDNYY2frcvWH00zfo66bld+ZTfFN562sc9FeyimJxk3y4wbZuAnHGANT9n9q48nSJfssIJ6y2tgHu24UcaPiIiIiIiIiEhPHbuMHz/MK8mYYWOHUiC9nxk/77BVrvAO7k0/mwAnLcsiy6w2SxrttJON08y6eLfNMg7fYUebjr92EbNf+pz9PGelEx47l7POxsbpj9jzrNiKaRie4QtbAU+iQ8m6CbPtr9vtzpMAgOn49+3at/QXkNvhNRO8yEo5sJnlZmDvxlZhs9JfaC8D4V4AwDar029Hq7kyblgHgaujFXx1fobrlyw+xin3Qa9yv7L9CF7KTwEAIpczCmZtjJZajP7oHwIATH7X4iVuXb8Tv7LcIRn3up9km3CCmRMFm+GS2WNPNS2QWqxsB2trrs3s6+k66/KMWAOKp3uNRw2uje0x5ardF5csJpM1i8nLXNGIzPjJmTU0XBkgnH63Xegb/9huderFwsi5PjPi+9Um1uZM4JmEdv+LaQnwRKbt3HI7rvKI2+0z9v76aXA7SzxJcFhhe2I1fVq2R8nA3vtsjdkcDX+Ined1r2O2MkK2/kEAwOziV/lqPRtVFkHG/mrE24J1MDLm/lSMj+eqCcLQ4mA6svu2GEM7Z60G1JTZGbtrjLulCrPa+rbA7ML0lN3yIB/sVlxe5Sp8zRFnU2fITnzMvrj8G3YbdUrTovCTmZZgA4+VYLGxzFPgIk+g/No0xYgn4LbM7ppyiNSctLHKeM3amu0NaxuuZyXGrOXTeF/FmGL5TGwxM94zfWYJa/+s50iW3s5X+eu8VXbqIvFxzgazxVZ4omACaxQ2U/v+U7s10tze5ymzkbda+3p3zbLXxyPGzqrFztawws6Y42YbKqNZ5bHczGK92rK/ip7ZbF8uP1IgrLzPvrj4Jb7a5nZ/XblDcv6bX408/S2x3Qw5bAw8CfaGf32aIlmyx1Sp3W5zx0xdWB2f3QHjZmRxs5mUqC9aWxbW+Jl8nfWl+Flu815r0xJmGU7ZNw4eGAHhLF/l1+7QbztfyvgREREREREREempY5jxw/2fyzabV2zYbXbSZqPzFZtVzFObZczadyKvbH/fAJadM2LGT13wNJ7aZhXbNVuNz05dxvbaOfuen8IzstSi5ZO2WvHwYx8HACQnLCsk5lx1bQeYvGB7EVtuti93/wAAYPfS0wCAF5/+i/YzWiG76xLGT8LZ6Zozzde5zf38psVCNhqgZZbGOOFKKmwGu2VstVwNDTNWpi9q5Ju28pEXXDlfYdZGypOYUpu1jl6Jnq9j0DbIwdXXjOlB8Ar0yg1bBIEZEw3fs7E3v1ywrCrWRJgOEGGrZOPaYuZ6YpmI7abFTsOVsjjkSvooIueKRrbNE1G4up9WXifK0x3tdsAaU/msRdhlYQ+tBSwczzJseCLXLk9LSb2QChct22oJkatk262ttl/jiv1WbfFT7jJexlzVGrXIr/AkQS7VB55YmDM+M2YV+kmYy7k9brkKCF7DzlNp1dQsFG9zImPGTzC5xvetYX2xMmRIMeT/Wz+yE+12c2yxU/MElYbtRpm0SKasi8ATwTJmjbXVwXjwEy0L1nBJJxGh9axCr34mi8Pjxt7PGeNmi7XfStaZbEODJZ70lfBEnVnJNmbC+nQTZu0wRiZ1iuGWjX28JpSnZfBQQgRLNmTuCFAwSzbMGsSp19mQRRS6bRX2Hpes9dN41h8zKr7e5shK+/xVzXiiJMc9E37thwXW/Kgzm7QYXLc+bcDsoJQnwjW8rvdT3m8uMelwULUAa8OozVlcLfuqMducJnodMNb6STOkzBBruBVih6dVVuWQj7VrlRl/Nm+AmV03+Pj4OsdPHMKk/nmeceTjnGIXew1TFzdHe6CjUb6IiIiIiIiISE8dv4wfzganrK/hp2ulYG2fHZ62dYWb1EePAlPL+Am5ZeckjT2m4WlMnniT7z5oX0+3ceLMBQBAyYX0NLWMn5WBXWvjtO2bbwrLBmmCzXA30wzpuv1Q4otmK1b/ZyWxfYbnn7espLLissgRn308ioa5xUCW2vs3rlhTY8qaGteX0GS2Ylqm9n7V3Cc/HLBOj58I5rU18oicB1UUm8zw4Vub7dqMc9rYSlvgCQZrPAUhLWss13b9lM/b4MId+m3lzuDpFtyXPOEqxYzHbpXRYueF2RIiV9vLhjWfgsXbqLIaC+CqSMJaT7GIGL1gd5UFV76mzPjhXvjipAUTF+7BhTKE7RY5X4OfOqgWZXFEP92CJwnuMm5Kni7ZBIun59s1xNoywsbR2phtHs1Vztb4WGbvMMswTiLy51gvzONmbDFQ8PSmsM4VMnZIJ0asnbC7ty8/cA1JcbNYuveDWVyz4G0NMywYD88mBdLEYqVlTbppYMwwUzXyZxJmEMZpxGDH/n8YfLWUq7RM8fHadL5OusxaeOm1BmnS8L5w8LXK3Pl70XKMMmX2hmftVPx3fyGLGLFd8NoubcM2Ycw6Ulwsr/xUp7rB6EVm/zBZe3+vAAAgAElEQVQDMWGGWMn4yGof/7AOHQdCyWaNEFVHbJHtxY71V1P2Tw37q5KZhS/FJSSNfc7y7PhpY21QPmWGs/dTjI923GLpJftexdOY6pptGU+hZNJrl9WwxnFOttMiZTwr42fxeNw07KvGrEO3y35nxjHv84MBwpAdy5K96bPcvk5ndtswW6f1pOi2RV7yZGQ2H+kV7rTYtpQffpRCzhMoeVgckqsRaWZBVfckbpTxIyIiIiIiIiLSU8cs4ycg4QkoKWcPc66sJ5xhDpt2m7T2/TS7D8nmPfa9zFZT09ZmGcM9PJWn5Mr6xGYOs/IE6o1vBQBMdu2ZE66ajXiNgjOI05rT1JXNjidlhiEzQPhSkfF0jeWGGSK5ZQCVlWd0aK3sm4+r4VwhHRW2oh54ysWMaRQ7jWXdXJ2uoOHJFzVXULulCGZ3Be59DjVX3DNg5SJXtpjMxcMvkHFWOoMFVMoYWR0xVsYRw027Xhq9xk8/9qMedd1JcJxnr7myvu0rYeCqKuuxXGqWgYp1NXgSRs1jck5VfkLGwfo9SRmx/qotrWaswRFYcyG7Yu//yphxwJsR9z+31xoUvj9emRsLo4sb1kwoC3vvr/PUktBYn1EyreJCXEJkNuqMJwiWvA38fvC6PXyf0xixdIEnE6YeS3Y7uMbMnnt5yhdX31kWD8VWiyL42lE/VsL6Yq/NYbZYzkzUaO9/01r7UTKT4/k0RcL+CMz+a/10lQFXU31c4vVW2ogTFfsrLq2WrJdQ8n+yUxZbCfu4JQ+XV8uuL1NrszgOtzkN42aXfVTL+ClZY+NKvld/x08fTFh7ZcDMn8g+qp3a+9xsNlg+x1pBrLMx3WGGT+YnTVpfltT2OK8jFC9OkbD2pYY3i+VwmzPjScbXW4udiu3LkKclXQgFksbiKDJjvm3tvnX2bQmzPbxGGOq9cU7CFI2a8VUxdooHLGZSZm6scgydXK2R+YDa+y3FztwdHh9XBU94a7zGD/sW1ji8MAwIQ2YVMgZantK9us7Mdc+E9y4ta7EamGHK095afsaqt+z7awyGYmrxs8agay/VKAr7DDfrcmWO9mlwx2ziBwhMdc5ZbDnZ8lRTGxjH3LZT1Zvc3vVyjrjKD2grdjvNLZqKZ1mYjEUx202OeqYBS0sfsOsxfb5ixzXJbSA0vsQiVBU7Ug6gmqbC+pATAt7ZtRZkzdQG4AkH83sJWzrO8m5ZzmzfzPbUPoRF7qOZ1RYLVxub3Lk4OYeEW3pSbicshvzAFryAuF0z5duXtBFbLzGm+J6Onrf3PF+ygt/lR33SiB/yV+z+E0WJwVe5RbA62o1S3/jYYonbAq+1NpE85RGRvsULnDS8cukSEsZVPrSJxQFTWuvE01L5QYp95jBEXD5n10mn9v6fgcXDPZnFzuUPse2bWBu0HCx2VpMZ1q69AgC46kU7b/N3ltvncTPgBPKLU+uzLjFuai5ApNzedf3lywjc5pkOuO2TbY5P2mTs8YfcnlE0EVvPcTKxsvd+4ymLm43C9jAnj/Dggx2Ll1G027VkhuKKPVbbdRZL5DuxlFkcvBKtPbmWWNsz6/Zgsc25sIkwsKK5xZq1F6PTdo3t3G65CwfLfrBAGnH5KX4wKy121mornjqc2bUufZjPs82+KbXHreYVmku/y1frRZ5l3jxuhmxzzje2wHU12GJj4wulrcVNeX4TeW5jnsHA7huMrB9a4rb0jAWil7ktcJQBF3fY5+X23t+7ZnGzsmSTgS9/xK4Vx9zizm2Ba3mD5OoVvlj1UotkL3YsHl6orTRGFiyGZvy4GbmoXl54CYmX3Bj65zK7lo9/Bmx7lnNuKW0iXvoGj+UuLSZOZxZn66m1Wy9/C7esjlnAnmPl0bDG4Jo9dufgGpjMkb8Hy7mNY15t7BCl6z4+5kQhmDyx9co5JCx1ka0wftbtZ3czjokYLwUXJIq6xcWn7XN1xgN4zk6tT7qvsRmgi49aXOVbHGNzcudUUWM42QYA7Bx6zUeVtnqJiIiIiIiIiPTUscv48eO4Mxanw8xmASPTUlufC2MxuXZlCHDGMTDdNXCbWOmFLTmrmHMeMEsStI2tYCTcQpH4saY8Fq5lUTtUnLlk6nWGgMaPX249jZoFfGcFfwcvUCZ3Wx19rvfgEZVlY7PENbMsWgzQRj9n2e7z47oTxljBY5JHTD8dpBE7Ex61zfTpFS/izJRYsLCdr+CvLNn9S23A9ElbCavH23yNR31eul8mrbUJni7qoTRjRl8bLXaqZNRldEUWuWxnXLViPHgKdMGth4OQIJtxaw4LIW4wNfYeplovWVIPlqb2/Ce4XWwYEzChbC+lWhbG1I/c5raclu9byQDyI9VnSezami6LkFtulgo/mp23vtKaRoT24FaNVfZvJ5kdi0v2PCO2TSfYh67EAJTcrqPV94U0Y+zUXlCeBTMnjKHItPcZgMD3sG3Y5kyszclHLPLtq6wsqlokEQW3BHlx53uYgr+S2vOk24xRnsA9YluXl2M05av2zagM1UXjx7XX6cGxb9341hsW1AXQekfGWPLaywOOjzP2URnHO4MkxSozBAtuHTvLa6xO7Xl2n+YhFjsWGwNedFhNUZeX+CrVWS2icWvjmJKHEVQcf+yNe7iFB3u7Gjh8Rl1xHM2M5gFjJveMnzRBwQTBIX/mHsbdafZj7UW7I+GWnSUOakZJDcy8PIbanEUz8b6KaV+RW46ntccNd88EdOONhuOdhuPjbMAUeB7NjqGXTQkoWPB5mffdx7bnYc4BnGAftcLj3k+xjVpBxJAx3RfK+BERERERERER6aljlfETELripYEzy4HFxFBydbP1rB7epklX6C7zo+D5dc1jbT2LKOdfMzZAxQwNz/TJODvt2UGBhcfSyu/3LJ/QTcclLM6acAWl5bHxTatj3O82jxufYYYXyeTKV+3H2PpKalIjtpZG0XK2uGVRQtbKxICJWyOGXhGBglleXoNunZk/65x9HpzjYxkby16rbrfG7MJFew11X3ai9kvFVcvKY4Qx1RWM81iKJUL3j92yhFBbQ5GyFnzwAqv80RCAnKtny1z02GDMnORK2L0XeD+LbK55xkjdYJVHXQbFzMKpuLpVMROn5oppxdvAeKritOskuoxTsO7TGvsu1pzz2wwRiR+ZzKLga5ln9nBVnrXrPG5O8PVkdY22ug4AiKoKtWC8tiCL6HI8UzOzeBq9iLtnbpSIDducmul/M+uvMitRh5S3OUsMpu3esdtMPMVJtj0rbE8Glzh4uW7xmPG0i8nWRTTVNb4Gxc7i4NjWM37YBnhCX42471FAjLNuPBq8r2qsr4pDP1KZhaL5Qy2AZa8X5VkbHAevcmG9foV3+FHLrCFV7+wicFwli+Zg7FTJwWLPezkT1li0KIHIzzLMho5euNsLihWMNz9aO0QMatZ7ChYb9/D2NHdTZJfsGsWM/ZZnFNa7iLVl/KjNWTwVawdWPGSCbzNKhlH0+MIEiNzVUFufFUvLaG2X7H2NhRd3ZhZrbLvPVMssAn6GfddZNm4PXLa4Wd21768zAympxhg19pnKx8dHfZSsjB8RERERERERkZ46Vhk/CKHLzvFsmgw8nYlHKYfGZg4THrWcjGsknPkLnDn2vcpTr+nD2eicM5SxsVo9ADDw1Q5OEfpM27Bb5O+mM+05ADAZqHtzePgOGtZraBpldNxtoXvnfI+7V5r38wJ9dYN1n2INq5yAboUqae2NLJj+NUi9HgdX4WPsTi9Y4uU3eKrBmmdxbNptwYWRgsedzrZqzHZs73vk6oksiuTAbQwHj8Ztu3/pTP1CDbDej6+EBZ6QknC/esIVK1/Mim3EgKscq7zcOh/LhXrcx4XSJZ5COPSFsFmLJbaHqvGzSA7GTcsjlIPXo/NlUNbisQxDroA1nhXKkwR5GpzHj9cFSmKLnJ3RCp9unbdrjI9TvF1mJzbiCZRtWXfxqb5o0RyMnYb1Vpouw8czfnjSTpwhMlsschUVlb23frLOkP1VxnjIqtidLniCTdcGn3WFqc5neCoTdpgFcN3GLq9eu4AYlbmxeHw86se6MzvDM3+6XB+vEVUCHN/ELmuDA1ZmYoRDWUOILZb4vQ3GyUk2H54p5nXEEmYZBobk5vUKqdarF9TBDJ82OVjLsO3Skz3juUKI7D+ij5U5zmFb47c+LknatssuPOVtDB9zsrafPTVjtiEzfvKaNYdmO0g8O60nmRv9wPGN1wjj52v/2uPGs1OBvczm6LtfmoOnRiYeajVrYjYNshHrpTKL7CQ/O51gPc17PEOMt4PKrtnMtrHMbKS+ZMSrBRURERERERER6aljlfETY4O64p7zytbBR8mQ99nG9bq17wdmAhXVNobZOgBgpbHvnWBtnxO5fe0nqAy4EppnEU+xxk/Kmi2Rs4uBs9JXued+NmH9Bu6nj02LJZ6MkfgpG5XNak5x1a6p/al3XQt73waJZYbVkafBsYZGzVX3mpljKSaIPDkg437UIli8bI+5ysEF+zWulq4PgYr1NQY8DWWNGT5nONF8wldfGU+r/Nl0rUCYPcPXpJXUxcKV8sTe/zHbhJwZGzW/v5fxE5BwdSNFxcdazOxy/3zKVbMTjKH1PGKXKyPl1OJuxucJXHndZmsfmJo4GLHmz1qO/MJ1Pnd9e7+q3EH2PqU8WWfqWV/MEm190zpXrEI9Q2CWYQprOIrcYmpWMuvQTwNkgbHRMGLCtgzbnj5mN14/LHpdj8yef4mpYqMkRXvO40Z90mLh6VmpjWumrBHmK6FtZnHhmRxJDAi8M09tLDIsbNyx4/W/2DetMstnbTmiusoV1Ss+vuFJKDNrbJaYubiS2/NvPGKxnDzyEP7rF3iMSk9WUfuBfVVm4xg/OTDhKnzjdcUS1pyLq0jSNfseT3HKRtaebI0sBpZ5kuAqs5mX8xZjnipY8+S4wabddz/H2Cljbplr0ysbds3s9Ah/4ZxqXC6mg7EzY7ZF4Gcs7688mSxpUgTPkPexcm59zBV2RTNmIhfs89aGARnrscZd9o98zEmeApXzGgNmfywt8dTKYgXVM9YvRsXOAmFfxc/T48YzBVnrh1tquk0VsdjLcubYB+xfdmY8MZm17HKe6rW8EnCNGfbTXe6c4YGka5Vda7Wx2Fgrmu5nACDPljE+b+OctifjHGX8iIiIiIiIiIj01LHK+AH2avykXa0DuydyNTXyRIsImw4sZyMkzNjYjczm8FO2ZswK8muyVkuS14hTrrCxJHnup3tx5roe834mfwwaP6ElAGN7gobZSeXMXsustFnHsrnG30ez1ndbE33PsRdpYr0LP7mLj6vDFC1sRbONV3ifzT5nuzazHHg8ymbJk3dqwEsipD6RzQr0y6wLlG5yBYQ1OgoGVmwbzPgatJqxmLqyCV29BHuTvdaFv2sNKrSRpyVxBTRUbB+m9wEAUtZb2a6sCc8GEWM/nanyVVruVc75xNy77PXHCq7Epk1E3lUC0lrA4vA4IdaLaxk3TVcfwffAVwittS1tzVVWroC16Vl7LI/K2G2szSnaiBn7M88iLPKD2YQNV1b9oJURs82KNu9ON5RF47HivCYLVzu7/spruJRAywyc0jKLscu2ZcsyLBKegrJd2/cHZcT4IjN7+EzDwm7XGKvBT2Vim5fzdTVlA7U1i6sbQ3RtTs1br8XCLEEERK6UB7Y5gTXk8twem3PsUrKtKNEgsv8qGFNrXleMmUX1zNqcIePT4wdti7TLjJVFdKPYabwgodcXiw1ab3MaHnXLz0vZ1Gq4ZOynxo3F27htMGNCe+TJzCOOc5aZkdiWzCDhy8j5OpIGSIKnsXbpI7fzq8odcbCviqzdFJkt2nbFwXw8VAP8DBxLr3PIn9mxuPHsw1ll90+qFrV/dhvzMxUzi1a9pi7jyfuojKfshioiY3Z+6F7D0Y4b9bwiIiIiIiIiIj11rJbrAgISrzzP6vHRa/B4xk/j9VEsy6auMkxbr9fDn2VWEJipkfuJGZxFLooSTWOzzm0VuucGsHckBldek8pWScCTWhD3ZsjLqT3P9u5LAIBp9XX70ahTve42P9XLV9u7VXafjfZT2YLXSImI0Wafm9ZmpwOzusbTl+1apWVZJKzDUJcBdWPfy7ky0Qy8kj0zfqYWiwW/9syfsmyQsL7Q3ukKshgOrhKEbrFpL1b2Pw6o0bJGS8N96xXbKZSWudFWfK9Z/6WsGowZRwXbqQljtvSTMVo/6oAZil7wo4lYTx8CACReeEoWAFfC2Mb4Slhg3MRujczf1wptZA0Df68bL5Zwwr5fWYyEmcVPLIEKqwCAEfuvxk9jYduSst0qEj+pknUZmhajhJlE7Vf5WvqxB/7oO5hV2B3WFD3LkKcG+up70iBy9b2ueXoc66xMNu20yGbM7MPc2pxmGNFctfHLCrsplkhEYJ2gnE+TJ6y5wJXYZlKgCOz3ok6hXBweN/x3nDB+/PQ+H+90JzM1aKLFh5fbSHiKUmRfldT2nm8xO3VQ1RgWPE2XbU6eekYYs1LZR3mmzyDl6XRVi/XkfgDAdnORr1nj4MXg/RXbGNaBQrzByY9JgwjLbG7YXyWsRVZOLUs+8PPR5oz1e2Y1WmZBTznOiUPfLcHPVH76smdusD9rG2A5sXMHr7av3NZvKnfSwbhB4vVuvZaXZ6v6h6y220WRMGunLS3Gmt1XAQAla7GOJxY3W0WDJrP+pmFWmZ8OmLaskejbf/h5PnhtoSbidHKP3dc8ebu/7EJQxo+IiIiIiIiISE8dr4yfEJAknkFhq6bBJxG50pBEzlJzL3NZX0Ld8HvdqoetnlYzZvgkPHWF1yqKEj7H3bS+N5DPyxXYurRskMgMj8hVtjYC08YyemYzmw3fnPyefV1/2R7brdbJ3RH2Th/gSlcS/X3lSgXjx1fKQoi2nA7As8f8n9t0ZrPGTVjl5e22bVOk7UkAwFJqqxo+c+2nfSWNPZYHqyDhqnxsGoSgjJ9F1P3b99jhfuHEY8dX4z120CDGCb+3xVuLnVn5PACg4QlxkW1PHSOa1GJnyO9tp1zt4KrqBk+ga3iiYO01h2LASnYvX8vAX4zMnWfyeNx4d80sUn//+Ga1qLradF2GKd/HavaUPYZZFuBJckmTAonFTZna6uqUtTomzPRZYbuSMm4CM4/aBlhObfU91F5nSBbB4TYneCZf9Axk5/1V09Ua62r9sJZPufmCfTtlhipP6QnDiHybY6EhMxN5ck/Fk3U8i6xglphncqDJMUrPAADGtWoWLorQrQUzi8LfL6+J6ScIMrM5oO5W4rvkZ2bT1+V5AMAsWLzsst8bNDUAa3Nq9lEN6/80jIFBao/NWfMn5YCnDQnuz98NAHi5sXFx1EmUC+JQ7LCf8N0VXX/lWfGhQux2L3iL5Bns5wAAkX3PDsc0edMgiXaK3Iz91cyzonmFzGM18VPFGDt1xAnWunuptgzVo16rpR88bg6Oa7wAb+jeI77DoUHw7B9minmyTrP7Ah/DUwn9s3nRAgNrc9rIcTDbntrbrcQz1Vj3zrNYG+DenBnxFe/zTNoj6lhN/MQYuw9XGY8zHQ0tmOpym4/ihEy0AXRbt6iZUjqeWXpgObF0wbL6LQBAntiAaMDbNB92E0wtAy9mfnQzj7Rko1VHS02b8oPerJ1gzIHWlOmI49q2eJXNc3YtdXR3WexS5gcsgjtOrQBmwvet6doue18LzHzoDTCWQmOxNdv9fd7BbTpMP92ZrON9yWMAgDOpDahPTe027FhDtsEzlpeGXtSXl1oKyF7U0cqLyNuclFvxymAxk3Ig3CYHCw627WxvSwb/qTettVPV9Gm7ZZw1bHOqyQBv54fwU/xenlvsbGf29ds27IPWoGCn6dsIRy1KvMRX68MnmT8WG0xsoOv1VGM32XtwQNS2ABqmSbfWn3kcleWLAPYmHVtOHLaTAu+MHjf2PIN8HQCwWdgk86OrVlB8vbBGbomjhrYABuA2j9v+XeVO8v4qY3/V+Af14P++uZCwNzOIhNtJA8dASWITQJPtp3ktjmUSLlQkQ3xs+AcAAPdyG9jJHbv1Lagby/b8y14QnEPOtbXTyFpfEJFF0Y2P2Ye0vq2Tk87e5sToB5BMEbwIK7fpxMo+zFfbNn7N+CGsSmzSuUwSfNfa4wCAB4O1NWupxVTkuHiN89MDFobOuLU+zRucDLas6kOuo/0RrE84zmHfUjfennBLVlfcmXHSlogc13QxVFmbMG1sK0/KUXTN8U4ZUnzf8L0AgAfYDq3uWqxOOBi+d9mCZ8j+MuOMZDpKkfmktiwQJl0kvjDpowkuJmV+oA63dbWzfUkYfmtj6mpicdOwAHzgwnmSZvhY8nYAwEOwcY63Obu53Z5Z5qJ64WVX2OasDFDA4rMv4xxt9RIRERERERER6aljlfGDAHg90yzzQpk2k5d2s9UsJBU8pavaK2TH2WkvQhU4CwimSDdcwWqbojv6tOUKa6x8NtP+5FvMAqmYBlnWtspWxhk2Z18EANStzV7W8Rqf1wtPKz3xbvNVi5Sp7D5j6gXkYpcK7T8QutXUrgB0YKzxsSnXqgKLQCMGNI1lgFXccjhjXA5am40uE5vJHjC9NbDAXVVNui0+XkQ6ai1sIezFjr1nCVOgu4WN9uDXbRu79PmEK6uJr3IypzXxSprMHorJDLNg1x9zo+kWm4khby9NuBWw5co90+vbtkaSHtqSKnPn2y7SnAWZD6++p/HA1wmaLkMsib7aau2IFzBMmFWWgVlnmCGNltGatIyl2lPx7WY2tbangq26VoybWVNh5G1Ob9bC+sFjJ8u54ulblXkb2VF5BhjitNv2kHiRVO+vEo8d8H4vplpiVlmm4KTmqntrWYaj3FZVm8yX3bm9lYdYxLbBQ8U7AQCXprYl6Kinz/cDt1twi5Uno4ZuOwS/Dl4AvurKJSTBt4d52QTfylzx1gsgBExmdsDFmNllk8TGtqPMMoBm3Iqa5uwz4VvBGrxr2eLmn05yfk8Z8IuBbQrHEmnmYwreRo8Pbu9rJ0gazzz0cQ77K14x9ayL7vNZgrK2LNMp42nKTq+M1k9Npxxvtb6lnttPQ4VTuWU9h8rHyMqOnz/GgG/Nw8FiyxyyIGGbFJu4t23Qj2hnIXF/jH+2ShkjKWaoGTcVs4RK35LKJ5gW9rMZs1W7wtGTFicHp+06Y8bSbf/O86WMHxERERERERGRnjpWGT8BQFVzNXzbVjkHPE09sFhv23jGj80GDrICsWn3LrDvdpD5ypcXimbmT0zQ1LZ6WkcvSucrFvY8ZbQVj4pH1s0aHh/fzjBrnuV17HptV3BamT7zY3/73doycpZZg8czffYOVmYtoLRAy2npyIyOBvZ++opIwh8qGD9pHGPSWlG7663VEMpbO555ygKsCTPDRmNfkbOLnK+vYByv85VqFWOx2PvvK1WD5pR9O/F7fX2Lq11FYMGWvRUNLzafdqsiXFXl9yMaTBqLr9h64V5rU2bMKNupLD42mDW2zmK943oXvz/7fT7Wiy3KoqiqywCAtHwAwF5WYZdIyIYkGbYAi8AHr6/QWtbGwFfVeLhAzuzVPNYIrAdUg8fkRvt6hytjz/Gwgau7thI2Sq0vu1Jt4XJr/VirVfeFNKstdoqaxds5hIjMFG2ZOZjlsRvneJahtzFDX8HnOIRDJuRxgp3KDipIGDtFbSujVWUr683U2ry1LWtzVq/ZT2/VO6gSjWcWVVlatnleWra5Z2R0bY4XfM+nCNEzenjLtzVLPG58FZ6ZibHFpRkPLWCh3gCLlwmPTd5mNs8qa/6MWL9l0s5wobbaQcoQWzQc57C/ykobKyeelcxdEF4cPs1nCExzTtnmpPBdDfZ+p8wIKjhGymPA9cr7GtZUZZtTJna7ObWB1ZDbOwqOmbbaHVziLgqNkRcJC3rPLF7SiRXgTpiV3NZ+kg0/PxXoCnsFP4qd4+CcWdBJa4/NPGu6qbFT27jm1dbarqVg4/DAgt9XK7Y5zGJeYvHncTvB1yr7TF73ZJyjjB8RERERERERkZ46Vhk/MUbUPPVke9dWvwetzeplftoJj4eL/HqtOIWEM8eRK6ANV9ALVgX3ugkNV+mrtkbNE5xarrQ2XPWo+fVuw9N5Wt9vOOY1StSs/7NXo0UrY/PmKwSz2laqdoKtZOZhh/cbr7exnpztvuk1oWqusg8yZu8wWyhjZleIM2y1tsJWej2N1uJ0FOxnnuOxzJ5lNuZx3y+3r+Bqc+HAa5XF4O9HzdiZzizbMPPY6fa+W5tTpCfQpRWyVotn/aUDrlLATwCz2GrrGXZai70p6z+VXN26BluB+zozfnK/Ntue7fYqXolfstcIr8Mg8+ZxU1XWJqQ7FjeB9S/2Vt95wl8+2jvipt6LCwDImaGY8q3PfB99M0XNGJtGa3M2vf9hfDw/tef3uJmxvXq5fRUvt7YS1qrNWSiHY2c65eo7TxaM3bHuNi4ZpaMuoFreek3DUc76BnyLM45VQlthkyeeVlyhb9kvbtbW9nylsczVUfB6L3aNi+11vFgrdhYPs5OZLVqNrf5SCMwmbj3t3dqcfDRAd/qOH6ncsK/y8bHXhIp+f4NX2G/tMDt1F9Y+bcBW33ci46arTWU/fCXu4Aut1cBUbZ9Fw7EKY6fk0dpJ8DbHHuX91SBdQeDnrdZrSLHuShrYX3mmqmcoxhaXWmvLxuyvZoydy8Gyxq6153kxu9aU/dWFeBXPt8/wlarNWRyH2pwdyyIO/AzkfRW4W2aAU90Wi5YZzE3Dcc7ATij13RSeEdQ0M1zj2KjiZ/4WFidbtfVhL07sa6/NWnPMfSVu4avRTtZWxo+IiIiIiIiIiCy04KfH3JUnC2HuqSuBJ3QliVd85wlL3M9XZNx/6qcnhQQ+P5bCvhe7mUebVmx83zxnsmsEJFz+qLsVe7tG6csi7V5NHwAoWUehbqhNjncAAAdXSURBVKevcxrT3P9sbyruTcvecYsQN91pF109FsYNTyjIuAqfBZ7eFmfdSlfm++F53yCxU3p81jpjXAEpCv8zxu47fHr72RlsRbXkXuhd1gAat9dQc0/sUYgX982MG2BRYscdPDEr8dOYEp68w1hq42SvnUp5uok/xpcy4O2YtVchZMiqg8VfMq7C+4rbhPWpwFWLmm3QrN1C5SfLHaGVsOPS5vh7HVjcJyR+OpzHhMVA02yi66u8jgL3q2eMrcCaCTnblRQJ1mEr877s6u1REez7m9FqajSsQbXbMusxXkXJ7CC1OXsWI3aMn+KFQ6d4JYf6pDru7J0Exu/t9W08VY616nKv1YKANWzY9ZnVmnFsVAT7mc3oWah2/4x91HZ7HbtdvY2jU6ul/22OO1jQ0vsjz0pN2K607bRrlzyWMt6XckzkNX8Ktis5EpxhZg9arwtk1xgE+5nLbHN8hb3i6bs7cRvbrH94lOqKHac2Zy92/EvP9jt4KmXbVl3sJF1b4zFk9Xs802cQrD/LkeFsuA/AXkaix463bVfZ5pTR2pox6xbuxi3M1F8dsFhx43konhp2qM3xXTmx7DLeE46FfJyTsv3o+ir+TBYS3IcH7ed5eqmnoGVd3FjmT8kMsRnjZxLHXSwdpUyxN4obZfyIiIiIiIiIiPTUscv42eMZHL6i4becneacWJ7sL4OUHLhdYtZQ02X32L0tgJyzlX5f4/sY/e/NFYyG+1D91mYUF+jPdJOOz6z0Qb5K2t2GfXOp3Z7mg4/x1dBu0/O+1TVfFfMTK7z+gdeKiqzBUrPeVI1y3+MX9s90Q8drJewwb4MOxk5EvOF9vupx+BqWi8aMxNgeeoS3RTwlgZkbkW2Oxc7RWclwx6/NObQK7/1R8Eyy5jWP9cekXDH1Nifs6/+W2B5FZm3stUo8gRK2Ytqwz6oOtDmKm8OOUux4Joe994fHRAdjx3+rvT9ewAiMHcZBZPQkXezYSSoN6yXUbHsa1Ecq08cdvzbHHc4A8iMp42ses9dXMcuwixuu0iNgjTUL264P4imW7KumjJv6UNy0aBQ3r2OxY8cdOhb5wDjnYLvUxU4XM/65LMUK6/943cOm64Pssd5feZZYsy92NEY+6GjFzaGMIOzFR5dV1u2eOPgTAQlWg2Wnel+0145wNw64C6eLK4+b/n0mV8aPiIiIiIiIiEhPHeOMn5uT7JsbiziYoeFZPa1Xs9/3t0y7+7gSxvsO53gcXik7qjQrfdj+P8fBdz05VOtl/3vvNRK6uOluD1617cmJb1oJu1kHV8Rer71IWHtj776DK2EeK3v7lI/2n0Ztzs3bi5vD3wdStjmv7YsOxo3anJvTv9g5WNduv6zLUD3YX92ozTlKNRJej9qct+LwuvJetmHBE3v2MprbQ4/0ePEsxKP9p1Gb81a9fk5CwF7twvia2IkHbl/7/aNJbc5b8dqsIHc4bl7bFx2fuNHEz23wNLPX65T27nOvN+R+ve8fTWqc7ozXfrDv96+uAdGddPhP2e9fXW3OnaK4uZMUO/2lNufOCIc+oN14nNwPanPuHI2R75zjFDfqq/Zoq5eIiIiIiIiISE9lb/4QuZE3Sj9989TUfs82yq056qnwMk9qU+RWKG7kVil25K3TOEdulWJHbo36KqeMHxERERERERGRntLEj4iIiIiIiIhIT2niR0RERERERESkpzTxIyIiIiIiIiLSU5r4ERERERERERHpKU38iIiIiIiIiIj0lCZ+RERERERERER6ShM/IiIiIiIiIiI9pYkfEREREREREZGe0sSPiIiIiIiIiEhPaeJHRERERERERKSnNPEjIiIiIiIiItJTmvgREREREREREekpTfyIiIiIiIiIiPSUJn5ERERERERERHpKEz8iIiIiIiIiIj2liR8RERERERERkZ7SxI+IiIiIiIiISE9p4kdEREREREREpKc08SMiIiIiIiIi0lOa+BERERERERER6SlN/IiIiIiIiIiI9JQmfkREREREREREekoTPyIiIiIiIiIiPaWJHxERERERERGRntLEj4iIiIiIiIhIT2niR0RERERERESkpzTxIyIiIiIiIiLSU5r4ERERERERERHpqRBjnPdrEBERERERERGRbwJl/IiIiIiIiIiI9JQmfkREREREREREekoTPyIiIiIiIiIiPaWJHxERERERERGRntLEj4iIiIiIiIhIT2niR0RERERERESkpzTxIyIiIiIiIiLSU5r4ERERERERERHpKU38iIiIiIiIiIj0lCZ+RERERERERER6ShM/IiIiIiIiIiI9pYkfEREREREREZGe0sSPiIiIiIiIiEhPaeJHRERERERERKSnNPEjIiIiIiIiItJTmvgREREREREREekpTfyIiIiIiIiIiPSUJn5ERERERERERHpKEz8iIiIiIiIiIj2liR8RERERERERkZ7SxI+IiIiIiIiISE9p4kdEREREREREpKc08SMiIiIiIiIi0lP/PwG0eoL1AX/NAAAAAElFTkSuQmCC\n",
321 | "text/plain": [
322 | ""
323 | ]
324 | },
325 | "metadata": {
326 | "needs_background": "light"
327 | },
328 | "output_type": "display_data"
329 | }
330 | ],
331 | "source": [
332 | "# Create progressively growing context set\n",
333 | "batch_size, n_views, c, h, w = x_c.shape\n",
334 | "\n",
335 | "f, axarr = plt.subplots(1, num_samples, figsize=(20, 7))\n",
336 | "for i, ax in enumerate(axarr.flat):\n",
337 | " x_ = x_c[scene_id][:i+1].view(-1, c, h, w)\n",
338 | " v_ = v_c[scene_id][:i+1].view(-1, 7)\n",
339 | " \n",
340 | " phi = model.representation(x_, v_)\n",
341 | " \n",
342 | " r = torch.sum(phi, dim=0)\n",
343 | " x_mu = model.generator.sample((h, w), v_q[scene_id].unsqueeze(0), r)\n",
344 | " ax.imshow(x_mu.squeeze(0).data.permute(1, 2, 0))\n",
345 | " ax.set_title(\"Context points: {}\".format(i))\n",
346 | " ax.axis(\"off\")"
347 | ]
348 | },
349 | {
350 | "cell_type": "markdown",
351 | "metadata": {},
352 | "source": [
353 | "## Mental rotation task\n",
354 | "\n",
355 | "As an extension to the above mentioned sampling procedure, we can perform the mental rotation task by continuously sampling from the prior given a static representation $r$ and then varying the query viewpoint vector $v^q$ between each sample to \"rotate the object\".\n",
356 | "\n",
357 | "In the example below we change the yaw slightly at each frame for 8 frames."
358 | ]
359 | },
360 | {
361 | "cell_type": "code",
362 | "execution_count": 198,
363 | "metadata": {},
364 | "outputs": [
365 | {
366 | "data": {
367 | "image/png": "iVBORw0KGgoAAAANSUhEUgAABH4AAAF4CAYAAAAi1D6jAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzs3WmwZVl61vdn7X2GO+RYmTV2dVf1qNaA1GpaFggNzaSBMMiYD5ZDBhubMIYQxsYRNg6IsISFscPGxgEGLAIjbDmMIYJwACaAsOxWICGQWlJr7EndNXZVZeV8pzPsYfnD+6x9My9VPdy8mXnuyf8vIuvUGe85d7937XXWete7Us5ZAAAAAAAAWD/Vw34DAAAAAAAAuD8Y+AEAAAAAAFhTDPwAAAAAAACsKQZ+AAAAAAAA1hQDPwAAAAAAAGuKgR8AAAAAAIA1xcAPAAAAAADAmmLg5wFKKX1LSul2SuljKaVPppQ+k1I6v2qvidVC3OC4iB0cB3GD4yJ2cBzEDY6DuMFxPaqxs9YDPymlH0sp/Y0jt31HSul6Sunp+/QzfyCl9PGU0iKl9KN33pdz/meSfjnn/FFJPybpP8k5376Xn3c/XvNR96DjJqU0TSn99ZTSSyml3ZTSJ1JK31PuJ25Oj4fU5vxYSun1lNKOTzJ/qNxH7JwODyNu7vg5708pzVNKP1ZuI25Oj4fU5nzMMbPnf58u9xE7p8PDanNSSt/nL0T7KaXPpZS+TSJuTouH1N7sHfnXpZT+okTcnCYPKXaeTyn9w5TSzZTSGymlv5RSGkmPbuys9cCPpD8u6XtSSr9TklJKG5L+muJAvH6ffuZrkn5Y0v9y9I6U0jt8vyR9g6Rfutcfdj9eEw88bkaSXpH0HZLOS/rTkv52Sul5/3zi5vR4GG3On5P0fM75nKTfI+mHU0q/0T+f2DkdHkbcFP+TpJ+98wbi5lR5WLHzAznnM/73VeVGYufUeOBx45/130j6g5LOSvp2SZ/3fcTN6fDA4+aOduaMpKckzST9Hf984ub0eBjnqr8s6U1JT0v6kOJ71h/1z38kY2etB35yztcl/TFJP5JS2pb0X0j6XM75RyUppfQnPeOwm1L6tZTS7/XtfzCl9PfL66SUPptS+jt3XH8lpfSht/mZfzfn/H9Juv4Wd/8GSb/i/39XzvmlE/iY9+M1H2kPOm5yzvs55x/MOb+Yc+5zzv9A0guSfqMfQtycEg+pzfnVnPOiXPW/9/o6sXMKPIy48f3fJ+mWpB8/chdxc0o8rNj5IoidU+Ahxc0PSfozOed/7r7OF3LOX/B9xM0psALtze9TfJH/p75O3JwSDyl23i3pb+ec5znnNyT9I0lf6/seydhZ64EfSco5/x1JPy/p/5D07/tf8TlJ36bIsvghST+WIt3sJyR9W0qpSik9I2ki6TdLUkrpPZLOyKN4KaW/nFL6y1/m27kzIKbJs/L36H685iPvYcZNSulJSR+Q9Ku+ibg5RR5G7Pi2A0mfkvS6pH/ou4idU+JBx01K6ZykPyPpT7zF2yFuTpGHdL76cymlaymln0opffSO24mdU+JBxk1KqZb0EUmPp5R+PaX0aoplF5v+ecTNKfGQv1f925L+15xz9nXi5hR5CLHzFyR9X0ppK0U2zvcoBn+kRzV2cs5r/0/Sk5L2JP3xL/G4T0j6Xv//K5I+LOn7JP2IpJ+R9EFFiurf+zJ+5g9L+tGH/dn5d+riZizp/5H0Pz/sz8+/Uxc7taRvVSwVHD/s3wH/VjtuJP2Pkv4z//8PSvqxh/35+XdqYuebFUt1poovYruS3vuwfwf8W924kfSMIhv144plF5cl/ZSkP/uwfwf8W924OfJaz0nqJL37YX9+/p2O2JH01ZJ+TlLr9udHJaWH/Tt4mP/WPuNHknLOVyRd02EGhSQppfQHUhTSvZVSuiXp6xQnIylGGD+qWIP8E5I+plgb+B2+ft+kKJyY3+bfT97Pn41DDzpuUkqVpP9N0lLSD3yl75e4WR0Po83JOXc555+U9KykP/KVvF9iZzU8qLhxWvTvkPQ/3Mv7JW5Wx4Nsc3LO/yLnvJtzXuSc/6biC/zv+kreL7GzGh5g3Mx8+Rdzzq/nnK9J+u9F3JxKD+l71e+X9JM55xe+0vdL3KyOB9jPqRTZPX9X0rZf66KiztiXbd1iZ/Sw38DDklJ6TlFU6rdL+umcc5dS+oSk5If8hKTfrVgf+F8p6iB8vyK97C8d82fmt7sv55zu+P+PnsRrHn1d3Lv7FTcppSTprytGwn9Xzrm54z7iZg08wDZnJNf4IXZOv/sUNx+V9Lykl6Pp0RlJdUrpa3LOHyZu1sMDbHNyeU1i5/S7H3GTc76ZUnpVESvDzXf8TOLmlHsA7c0fkPRfH/mZxM0auE+x85ikd0n6SznqYC5S7Cr2w5L+00c1dh6JjJ+3sa046VyVoniUYnSx+AlJv1XSZs75VUUhse+WdEnSL7zdi6aURikqldeKjvRG8tZxvu1vSvpJxQzZV+ec0z0GwjdL+ud+f39L0qS85ioE2Bq6L3Ej6a8oUhJ/d855duQ+4mY9nHjspJSeSLE97pmUUp1S+i5J/6YOi/USO6ff/WhzfkQxOPgh//urkv5vSd/l+4mb9XA/2pwLKaXvKn2blNL3K2ZhS90EYuf0u1/9nL8h6Y/5vHVR0n8s6R/4PuLm9LtfcaOU0rdIeoe8m9cdiJv1cOKx46zCFyT9EZ+rLiiWJpedth7J2HlkB35yzr8m6c9L+mlJVxQFmX7qjvs/o1iD+E99fUex7eRP5Zy78riU0l9NKf3VO176TytSWv+kpH/L//+nfd+HJE1zzt8m6T/XWxfV/Eq9Ium35Zy/XdKLkr73BF4Tb+N+xI1Huv+wIj7eSCnt+d/3++HEzRq4T21OVizrelXSTUn/naT/KOf893w/sXPK3Y+4yTkf5JzfKP/8/HnO+aofTtysgfvU5owVM6ZXFen6f0zSv+bXkoidU+8+9o//S0k/K+kzkj6p+ML2Z30fcXPK3ce4keIL+9/NOe8euZ24WQP3MXb+dcUA0VVJvy6pUQw4S49o7DwyS71yzs+/xW1/StKf+iLPefrI9Y+8xWP+gyPXf1BRKPOtvKpY1ZMU6wyvfYm3/SXlnF+/4+pSUn+vr4lDDyJucmz398VGgombU+gBxc5VxRrnt0PsnDIP6lx15L4fPHITcXMKPcA255u+yNsgdk6ZB9g/biT9Uf87irg5ZR7kuSrn/Iff5iWJm1PoAbY5n1AsbX8rj2TsPDIDPyvimmK08VOSNiT9lpN6YWeNfKdiJg7rhbjBcRE7OA7iBsdF7OA4iBscB3GD43okY+eRXer1kHynpDbn/FWSfp8ire2epZTOKXaD+nfyHUWBsTaIGxwXsYPjIG5wXMQOjoO4wXEQNziuRzJ2GPh5sJKk6/7/a5LO3/MLRuHovyXph3LOn77X18NKIm5wXMQOjoO4wXEROzgO4gbHQdzguB7J2Ek5f9Gdx3CCHBD/u6SnJE0l/Ymc8z+7x9f8/ZL+gqRf9k1/Jef8f97TG8VKIW5wXMQOjoO4wXEROzgO4gbHQdzguB7V2GHgBwAAAAAAYE2x1AsAAAAAAGBNMfADAAAAAACwph7odu4pJdaVramcc7pfr03crK/7GTcSsbPOaHNwHLQ5OC7aHBwHbQ6OizYHx/HF4oaMHwAAAAAAgDXFwA8AAAAAAMCaYuAHAAAAAABgTTHwAwAAAAAAsKYY+AEAAAAAAFhTDPwAAAAAAACsKQZ+AAAAAAAA1hQDPwAAAAAAAGuKgR8AAAAAAIA1xcAPAAAAAADAmmLgBwAAAAAAYE0x8AMAAAAAALCmGPgBAAAAAABYUwz8AAAAAAAArCkGfgAAAAAAANYUAz8AAAAAAABrioEfAAAAAACANcXADwAAAAAAwJpi4AcAAAAAAGBNMfADAAAAAACwphj4AQAAAAAAWFMM/AAAAAAAAKwpBn4AAAAAAADWFAM/AAAAAAAAa4qBHwAAAAAAgDXFwA8AAAAAAMCaYuAHAAAAAABgTTHwAwAAAAAAsKYY+AEAAAAAAFhTDPwAAAAAAACsKQZ+AAAAAAAA1tToYb8BAAAArKL0Re7LD+xdYD0kVVLynHOO+MnqfS/xBAD3Exk/AAAAAAAAa4qMny8pKQ0zXnfPRuR/aXYi3XUvHmX/ctS83fU7/+9w5gsAgActzkd1NZYkjaePS5Km03OSDmcL2+Wu9ubXJEm5X/pWzl+4W0q1JOn8xXdJkp54z9frZrMtSdrQQpLUXntZknTjzU9JkhbNgZ/dPcB3itMopbvzF3I++t2L72LAncj4AQAAAAAAWFNk/LyNaZpIkt63dVkbOWYsKs+ElfyMW81c0h1ZGp7Z2FevG+1NSdKi7/wYRp0fBbUiBp6cPq6x/3+a4s9sUvm6zkiSOrWSpCZFbMzSUq/MYuar6Vq/InHzqEl3jsen0ubEZU4xC69c4qP3/Vl9Zrb9UTaZPKZqPJUkjSYxoz6abkqS9ndvSJL6MpPeN3GZW+USWyVrIx+tt+H7aYvWWsnM2L70TknSkx/59rjjm75bktTMI2aa3X1JUtXOlD/3S5Kk7rU34vLNVyRJef/NeGwT/SBlMjceGY6jx7/7hyRJ2x/+aknSxfc/LUk6/9iWzi4j0+fmy9clScvPvipJOvPyC5Kk/MrHJUntZ35ektTPb/jFaYMeRSnFea0andflr/u+uG0S57bJ1pYkaWMacbe7G23Q3ucjhg7e/DVJUtfNHtwbxingfrbbq2FFRl7/715k/AAAAAAAAKwpMn6OqD0W9rWbT0mSvvPcu3Q+R/bPqPfad68pvVhH5sZ4FPenjbOSpNfrVv/weow2/8LtL0iSbi13JEmZma+1VHvU+LmNWMf+7Wc+orOKWYqNKv7Mxh5mPZ8iTnqPKC/GEVc3x3P9+PJfSJJevBqzFgeLPUmHcXO4fDkfucRpU9amj8ZRO2O69WxcP/tVqicxizWebEiS6hQzpPPNC3H7ImbSN2dXJEkbe6/r5q3XJEmLNjIRO8dM76ygTWcxtq6b0DmYlrnTPDcn/wFxn0W7Md14RpJ06UPfr9HjUY9lfCbOTaNNty2OiX5nN565F+1KvXdNm4uYCZ06W2NrN+JIjrErPmXt9fEac2cLderUObZohU636fl36Inf/rskSe//vd8rSTrz1JOSpF9+IzLBmltx/Jvr0ZeplgeqzsWs++i5iKH0RsTM6LXo98xfjPPZcj8yOtou4q4fzn44/eI8dv7575AkPfnv/nuSpPrrv1GStPFMnN82Np2tWiXNrjojfhZR0O35/NPHbPvWh98dt//z90iSmo//uCSp3XlVbTe/b58Eq2E0iozVM8/+JknS09/9hyRJm+99XtvvjHapr6PPXbshGTURO/MqMhIPXozz2Jv/+B9Jkm7+3N/XfM8ZibnUJMOjYjSOmJpeeK8k6fxXxXlu+swH4vJstFM7L0Tc7L3wCUnS8uan1Pe3JEmdV2T07en+Pk/GDwAAAAAAwJoi4+eIqTM3PrRxUZL0vn6qM33cNs4xe1q57sYFZ3LUvX+NOWa/tuta/8oz3yJJuq5flCTt3/ikJKkZ1pnGMPVbjxgyF3banHH210fOfZ0k6f39e7Tl2lCTLsZXk7Mqtpw5VmbLlzlmwjbSlt79VKyHvzWPGGi6mCntvO60qiPWOs/gZ9eQUpL67u66L1hNVR1ZPGee/gZJ0vnnvlOStPXE+yVJ8+13S+OInZHbgtEiMjW2qjjuW7u3JUmXbsfsxKUbn9Pj+XOSpHYej23bqOdSO8Pn4sS1pdy8zDzu/4VuoX9y8Om4rV+c4CfF/eFMn+2YDX/+t/2HkqT5+z6sfMZZXVU8pk/R5vSbcVzzImJh5MuNvV29/0pkZzy1FbVdnr0ScbRx8/OSpJtttE+zxnU5uoirvdzoV9vY1em1Pm5bsgvPqZJcM+wDf/LP6x2/Ndqj8dnISL0+i2O5fzXq9SyamCXvDtwPWlZqPItanY/nTDZiNn7jXGQvPnkQr1Fdi0zF5f6vS5Kablev+Xw4z9RBPM3OXoy4+YY/899Kkp761sjW+eQijufc57J56T93WTvuU8+aOAe1y7iuzv2bHHE1fu5rJEnbTcTpmZc/pRdf+Il4Dlmqaye5LuaFr/kuSdK7/+AflSQ9/hujX7wYT7RbRyb9opSpc/JO7bammUbsaBxt0jmdlySNxs/q+s//LUnS/FZ8H+u6snscbc96q/TkN/8bkqQnP/p7JEmPfXW0Ld04+uPV2egfP+6v6M3t3ydJaq/ONd+NzPrq1uuSpINfigzE13424ung4Mr9/gAniowfAAAAAACANUXGzxEbrrvxdBUzDOe7XhudZ636yKQYOdOnX8ZsZ+vxs3YeQ4XLzbMaXYqZr61R1FwY1ZG50Zfa4RO/RhPPyc7WSDrcJSz3JYMDq6oq69ud8fPs6FJcn51RXeLGM5qVd/WqnPXVelevvo3LUV8rL+P1xq4PVFdxmRTxODoTsxjNQdRK6NqYhU8pKSXXdmnZvWCVjbajJsvGs79FklRd+lpJUju5LEmap8vq9iJm0jJiY+xEivHCWTy7Md21KI+bTfS+HDFYq2QmRvbHVhUxtelaZLmPWOqrePzVUdInnbnx2XlkEDH/tbqGjLF3/VZJ0sWv/7Ak6aXJZTW9M0nnPp/kOPYH+1H3QMuSSRi39/2WmmsRU3k32o/RPGLqrGflz/Zuk1LUndIo4maj2tC3bMZOPX/fmRy/0MbuO0u3bcTRapucj5p0T//Ob1J7PmbKr3gG/brbmMbnuM4ZG50zVnOT1O5HX6XK0Z+p5DZmIy4nfq2LlWt2jCLz56k00pvjiKePz2JHsCt9nLe6kg3tS6oBrbJa1aWYOb/qdmnWOk7OOlPQ567WbU/qpMb97H4Uj8njiBe5v9P8WsSEnGW44eyNZ979ddrYidn1F29GZuKB+1PEyWnmPksdbUL1zqjDsuOYOrgV7cxCvdITziBzqafedaLq6BKr2Xct1oOIrfE4Vm9svPcbNfnMT0mS2n33c1y3bqihedIfC/dBfEv+0o853Kmyrjc1eiYypOfux7x5PWKqcV9l9qpjoPNKDbdJZy9OND0Xr3f26cgee/Zy9IHO+jveL/7UX5Mk9fl0ZMyT8QMAAAAAALCmyPg5ovYa0+uLGLl7Y5xUe217NdTjifGyp3TujmuSFLU1FtVC9VbMbF18Z+wO9vjjMbt/y6/Vphht7Lq4nrzlU1X3qq/GaPTua78q6fRWDn8UlJ2ZJjlGka/sxuzThbwjtZ7uLIuQU4wsX1aMFpdZ8aXv30lL9Z5VHV14QpK0eSZirHFtH5WdDByflUe+kzr111+QJHU7r/rdMX+xWly3Z/oOSVJzELPg7RXvuJQi66aZNOr3nbGxWPqZ0baMtmPmc36zbLUUcbC93FfrLI5J6wwf144ad9HWtM7waTtnC8mzXfVIHz77IUnS5+dX4zGifsLq8fE9HxliZ771d0uSrjhTY7l7VfObkb3T78T0Z/JucO0o4kY7Pub7cVk3t7W3iPg4uBE7VfS3I2tnexlZQotRtEWV64qV9qxNCz22EXWp3jOK1/gV79q0yGSrrrLkbMDtj0TW2KtblZqtOPccTOK8ceAMje61iINmJ7Iw+utxmbq59Gz0b7Trc9wtX96c+zGREbaxiNd4Rxvns6f6pS5O3Ddy7bHPtNclSZ/ro37ZvI7262pz/QQ+Me6X5llnZXx99IFun3GNwSragG4a57207VqHnZT34v+bOs4zrWvY9W9GvbH8myP7tftctGfdy26Lbl3TM85ArKto015yZvyua/6UCofUjDo9SqbP2edjF6/0wd8gSdq7HMe4Pucs5TzWeN/t0txZHe4zl12+0sXoKy/2oy1a7rovtTPX5HzU4NRB7Cq330Rbs+z278fHwonwd6JxrJ6pqrOS+xfJ54jxJDIF2/4xSZLLq2r0WPS1tz74bj32XVHb53bvfvAk+k3ZWYcj1xvrFvHkZhQ/dzdJW09G1tjNN+LnzNy27fSRMdufsl3iGPg5IvlkMS7LrbqlKp9Qxt7+uHzZbpzWVYo9l3TnrLGWG+VXGw3aZCuCa1qW+1yOIO7La/rxVTfX9Ep8gd99/VPymzjJj4gTlEqjVFJVvRywy4shboalXqWYs/Z86S9Q/kKXq6xuw6/rJRp179T5adyR/cVfS8dEOdl1S3VdnMS08wW/Ozo+qySlUnA3rndegqVc2hrHzqgZtmBPtTs3Xl7aJS8TdJHnpm59mTVuo/MyzvGYieNu6thsul3/uN63R2z1VaWzIxe483skdFZRHJvxdgzEjLZjM4FlKWrZtepd7D2X2YiRl1TMIjaSlxT3dTyuG1XqZ9Fu9MmPSR5sTPGYTcdTncsgZFneUw0FxJ/xUtRLKTpTB9mDmRSaX02esBg/FctOxxsjdS4IfrjxRFxr9/2F2gOE5XaNRso7XqreuL9TecnOZnSQJ156OPGTNn25raTkSa/awZqqGBTa9Pnw5mac6641N/yuaJRWUX0m/ubrccRA6/NaHhqhMlBTNrmQGhd+HuYXjjYTtzzIfBAPSJ37WaOpLjiGesfwwfA1Jtqr3eEa/eZVVwagJ+djadfT3/GvSpJ2no0v2uPHvfTLywbbplY+KH0i97nL5cjtlpcayl/k5fIJua3KKVSjqYvRe7lpOywX5Hy1alIVfdPL7/q9kqTzz/12jcYe8DkTx3brgv/2K28isB2xsPFcPHfrCamZRn+pdqH4PIrvTtlB0Ze4Kd/nR+V7vbRsHVtdWULm8i4unzAE1ik5R7HUCwAAAAAAYE2R8WNlvK4erjs7o29Ue+Z8Mjw4RvUWQyZOeba3P1WvN72sZ6d2WmIdz04eddSFSEkrU7Np6iK+zYGq5CplZfYdK6v22OnII8AlbuZ5prHjoWzJrVTui9vLcr/GBciWVaX5ZtxWMsFSyZr2X2p31ilBTbndcdUslS86G+gVsjZWUfYxzT6o2RkVJW01+7JPB8qlZS6Hsl760ktoXDU1daUQalLjbdwbRSbiclgG6BTW3jP3TjkaeQZ2lHslZkdXXilUOLkQyyDKjFRfMjLygXIpLlh5prxyCrIzfbLPR3ImWa579Td9vqldKL525lkVl7Uiq2fsuB07tT6rV9/dkiSddTbQZW8PfsVdi7lOVwr0o6JsIDG/Fdleoz6ran2+cptSlazSA7c5uUyX+5xTSVq4uHxfsnbuno2vvQyndiZa73amzb3kZYG1Mx4vlCzXFH2kS9MopPkzKvHGCW0VVaP4W0+Ns1QdNm4+ht7x2Jepkxpnj9WOm74sZS9Fn72cJ5XlPK1n57tKG97QYtPny23HRcmcXrrffECm/GpLI9UbcS6bPPFVcflMZCDW553pMy5Z0X5Om1WXzGnfNSqJGqWbXZqrEnmOqdxldc6QH2/Ecp9+7LILyziPLXsyflZGKczsDXMee/e3xuVv+iZNNrxyZhwHfVS57/J4nJsWVfzt19vOgM77w4ZKw7mqpK663SqxVrJhxhP3kxdZTvhRrt2X9sqdwyShkuV4OuKHjB8AAAAAAIA1RcaPlVot47L23TMQOaVh5LjNZXSxzCzEqF+ZVyhLSvdGtfYnLkY29jrBSYxEVqNSxMUZPp4hreqY5aqWldL2eb8i43KrbuSR34lrG9T1Yc5Y9vEr64bLGvfWs6CNpyiWfko7qVVvx+uMU8TJ2Fu9J2+trJIZ5vWp9SRmRtJsoXQ+4qbUkslMkN4/97CkN5W2oMxm+dCWerjVpB1etmT0VGPPnLtY72gjWp2x38hGNVZ1UJ5Ttl0uM6GefXfGxrDFZSlMXk9KKZihHcTqqUbxt7/5mGdJfW5ZzCI2Ks1VlSKDpf6c64wlF5JP5TiXjIxpr/FG/P900+vmZ87oaOOy1IiaumJifVftjnjd827rHvd57YxrN8xPWdHDR023H43GtO2G2fCucUazpzmXLjRfd6VGmesRpk55x7FXMlM9m1o5o2PD58epz4/JXc5W1R21E+O5ZWON4dzndqpE2+mYS320pFQpHbhg/J7/1rdcW66ch5xBOCploDqpu+nCz96KO7nz3LqNaW56Q5Vdt1/exKDbn2vkjs3U72FzyIyP17hdav/Q/1lRzuKqp6o2oyZLcgbO0u3GdKOcg5zRPHfmxjxps/L3MMdX1bpfM/djncExdnH67Mu27bRwqIx9Lu1dHHjktqZR2dad1uZhG/qp44iRyWZk/uwtx6r9fShVpe6uNzC5HLcv5iUmfDxnBzr/nlhlMymZYY6T3vXGNs66gSrf811zc9RkLfqSyRoPqd1Dr0t/asj4uccP/YAwsgAAAAAAALCmyPg54vwodijo6tg5JekJzVwvYb8vNTli9G+SYjvSxnUMklcxL5uxvtDFrOwNz47OZmX2w7vzPO4Vz5sxst16y8vx5bM6++mn/HoeRTzRT4iTlEssVK67UT8vSTqn6TB70DmVY+Hh4LaK2YbGtTOy16L3i15Lz5r1C8+ceqS5rEmez7zbhWfnNY3Hj86PtfnSs5KkGwTM/Xes37FnNx+Pv+/8pHf2243aTLnzLNfZLC1LnY0yo+5sjH3X4fBMRj+LLbh3Fre0kZ6PH+Pdmebern3udcdPjp6UJLXJW+imw514Lud4TyO3YQvXCcLqyD53zJ+MGbCtrWgTtBvH7PxkqgNv097dcN2essvXE6VCXRzXsWNgM830nieijbno3VJ2h21yI/PiA4uImw3vKDcpGYwpaZG/RpJ0Lb8Yr6erkqRZJn5WWjnnfPrXJElbGmnL55zd6xEbk9cjDh53ZuJN1wNavPCSJKluluqfjizTyTheb9vZF+dHESNfU+rzuNbUwqlBr6VKH0yx1e5c8bqtY3PhfZmueIdlavusrjxK6t8T8fFu91WeuR6Xn/WWx2On+kydvTptk27uRBxcfSkO8u6vvCFJWr5yRZJ0eSsymae6Jkk6P70uSbp4/pZuvRBt2yt9PPeKswpv+Ty3e1qm3R9ZJcWvGnYnbc+4hpN3A6wuxq5eG84cveCMsEuTkV7+lLOdfb6qnNpVO+Pnnc+/ORJ0AAAgAElEQVTE/TdvR1zsLiJebo/3tO3M6V1FnM3HEUPLRKbPqsnOWO8br2q4Gf3lvdyqX5bacnG8ts74sRejz7Jc+nuTM4IubF9W3nQWtL+vT7271/isd05O5Tv6sO1uXE6SnvD/70+cpfrV7ottRG2q/v8r2xOeDmT8AAAAAAAArCkyfo44cDbGjYnXE/YXhoyMqqwtLetB25ip71znYJRiZDLXm6pGMTpZe5ajXPYeORztxYi2Fq7x45pA44l09qLXJ3pdvLr9E/2MODmdZy88+aA91zR4VVM1zvTpvG69KrtNdHGsj44R11Wt2jUyxh6VbssERBs1oM5NXTvKs2i1MzTqea+pd0J43XWj+lI0BivCmRRz18zw2uK0KGvRvdvXXne4M0pb6oo5wDzTkcvadz+u10jXqzj+nnhVX5UYiRtmudTX8Pso+xSmqfbKpiplETOTpqunzG75nHH+tndBejPuzlUv3Yz/b3d8n5+6u+NaGaVUmM83W9OkZR9xMNuN2bJqEVmvlWsoXHMbs+HtUqbDxmBJnTMemxTPuVjHeXOze12StJ9P10zYI6NkRSziPPONn0uqvEXJ7Vcidq6/4FopV+Ny+lLEwe4bES+jnLRzO/omG5MIrHPetfTSJC6XpZ5ddmazK7NkTXXLs/mNIu5KtmFfjf1a0YdK+2V+kl2aVk6Xtf3ZaJee+0Qcn6edZXjZ2y1tupbhpmfhNxrpE5+MuBt/PjI+rr0S2YR7t5xV6Ex4b6yjqfs9m1ubkmtAlbqKZ3yyKrtilsz8jpPYinL/Y7ytejMyjSejuJzedIbPJ+PYnfMulM+4CXgySed+xd+ldt03ipDRyFnSl78Ql9duRFzeuBmXV2412i8l8Drv6jWJjMXFKHb1alvOV6siOSM9+/vT7q5XN6Sx5LZEznwvtTBr93/GPmds+vvY1qTXY7ejfTi46mygJu7bcBbqchRtUVq4bqt/7rhKqsbx/7cXrrF5KVZrLH792gl92geLjB8AAAAAAIA1RcaPlZ27dpxx8UoddRQW9YVhB5/K9Xo8kaFFH6PFZWZhVMeMe1VvarETI9eLRYwgd6XCfC67h8X9fdkpZezdnKbS9F1xWNIwX4tVVdaF7jkmbjgzY6eaqikzmLnUxIjH7HZlprPU3ShxNVZ3PeJvMfcuFl2pJh+P3WwjxprOtV5Gnn1NvTbGURuhKrGl2Ul9TJyIshY9ju3UuzFlZ/H0no1Ke82whU3ZPWDqGhndvOyC4rahi3jpug19RhEbbSq778R9I8fXxPd3njkf+XqVJlq6HlDPrl4rq6xn374Wx+rxzYifjUiuUdc32tyP+Ohcr6V2Zkd3ULJIPfs+jnPMuWnS/sTZp84gms9d66WJ2gilJtnU3YWp46uWtOEsst0UM6h1FVkaG84+I1t1VXnWfB7H+Jt+vNNWF8eyeT2O/9UvxOVnfQgfuxXns5t7kXGRctKLVbRlW94R7NIkYuUxn5cO+oiDZY4YWyherFHW7SoyphvXcpiWfpVf88LmM/FzRMbPqqqy9OxLcXw+8jFn+nhHnfNOuNl0H2bTyRRVl1RdjxnzJ25GH+XVnTjmry3i+mwZNTbHPkdtewfD6f5IGkd2yMYQN9HvaV3r54xPnrf7vZP7oDhBPn9sP6Pp9nslSVvLqJG59Wq0Ix+8ErH0RBuX73HW2KUu631XI5AqZ3VMS8a0s6C7V+K8uDOL597yTmGfmy31qUnJXo32aJxdN0ZRY2rmupukPD9EZdfIseumujZlX9KVZ0MZS1WlzlOUulT3yTjm9a77Sv6yfi5JX/+Sa6w6SeeMF0SMS4bgmWh7NtqIkW1/f1OfdGM73tNOG32vyaW4rF6OTLGf9XvuT0mGMxk/AAAAAAAAa4qMn8K1LRqvH75Zexel0SVlp2qkvtT4iac03WOSpN5ZPKmO59ajTW2XXXmc8VMvPFvloi3T2ruHedRxVMcM2cY06ew7XNk+lYwQrKqS8dM4Jg4cK321rcaz671HlGtfn7k2VOOZqVw546eeanLgsVjHTSpFfhxj2znicuG1yCPX8xmlTtvPuN6PZ+hbJkjvn5IYc4yJoXHj2YgD//Ev4rJv4oDN9pfKzu4YOXa2vJvAfuMML2f6jDyjPlKrq6Noj9ouZj6Xnp2oPL5/JjlDcYjHqMMxGo1Vj77gz8VcwH11D3FTOwP07E1n/IzjOG/HpJOaptHCdaI6X45cf255UN/18zfrOM7nJpXyVsyoNYtol5ZtnMdyFy9cOXtj4t0tazdJKfW6XEdMNc4uq2vPqLYRi6m77o/LbimrpfRp4vK5T7Q6kz3D6dnTZ26WmmRx/dI87r+6iHjo1A/z41PPxp7zuWzDma+LSWROZ2fxNC5edpBrzetz8Tqp1MCLy3kVrzqZRDxSd2x11ar07M04ts99Ktqjx5poc570cZv4fFf7dFflSl/r3SqfclLyZWdtbPkxr7peZuVKiBtlh50mazR+pyRp6tiddlHYY5kjDeCJEsYHcZ1d4VZLqd0y3XpGm3VkdZx1Xbnz1+I4f62zd550XDzj6+e6rHc7FOqD8h3LmT7uK3tjSzVtPPD20plBS+mN7EzUOs5P0z5q0r2p+Pl7VQRk25Mt/7BUY/dLt6NfUisuJ9OIm9GsV/YSi9oZzht+7vJV7/i2F7dfdH/nsU76GmewVs5s3hgyECNuNi95p1PXuhu7y9J1WTfO+XzmDOrkFRfNDX8P8/f35SmpEcXAzyCCoVM0RK8vyrKI80OD0vugV8kRcTYCtHw5H/UOqHapzc9Hh3jkk95m2VbXy34uXPNrlC9hfbRW02qu0V58ud9UnOCWeu3kPiZOSOk4exvKJo73wTxOJG1/TnM3Dq2PsRw3XSoDQtFhqt1W9It9Tfd9QvJt0yNLfi546+a+jAepDADNNd6P7XHP6H2SpIW3VqbHfB8c41daliw847/vp10orlrEN62J4kvShW4kuShqaS+yB/g2vf3pLb+BN6uIuxvVGV3pIm167pNPn12szjFSBptz71TpsoysafTE9DdIksZ1LK+QO9M4Yffwp9iX7U2vxRfjdy4jfp7u4rjevHVe+8v4srPvdYO9B4u+0QXlk4vGl/broOq0N4nXfaOL7tPr3dOSpD3F5WuziNe2FIvPpcjiUmenXxc/p4p4SSNvy9x83g/99PE/MO4j/+0vYmAuXTnQtHR4HSJb/nL+3lm0S9tzDyS3XsaVWn1rHzGz5fapFN7d99KvW/OIi8+7gPgr+TlJ0q6e1Sg7hd/buNclNnMs3fltz0b/Z/KyO9Xd4l4/NE7YuH5cz219UJL0nPs7j+3fliTlUQzcbfq8V5U5hb7T5SaWa+04xuZuw2rF7d+7iHZsJ8Uxf8OjzVcnE72h90iSbijapZ0qqtvv99H2vHPLjezByyf2OXGSPIhz5ru1nSNGnlpEG/PBKtqPDS8rveQm4Wkf/wub0o6/9E+bsoFBWdrupYbTaC/2lu4HeVb2fL6sr9+PweardUxULOs4l9bpRUlS279ych8Tx7Kx/SFJ0mgcf+dq4pjl/ThWy5+TspeTTjzIXI3L0q5YwrftL0jPjiMmPrBd68zN6Gc/5rg558mJydRFnhu3Qcsy0eBNnCQ9exDxOM8RnzsuJn21je3c27b0q04HpncBAAAAAADWFBk/R3SeIW2cRtq0nfqyP7LvK0WXcx+zEiUBqPdooPJIi6VTBj0LUpb7JKe8N55dK/sxlwLAo6pVPZ/4dU/XKOKjyZlinmSaeZlN0yUt+3KfC5A506dx0eXsY1/7NbIqzZ3SWpKESkHxMkI770u8lHVczkZLSZ0zAFIuf9b3sK4E983UM1BnHR/Jy3KmLl66kZeqy/EtqaWppJp6e2Q/tlxf9K32nRGydHuVHQdlCUXT3b1ssCwBayRNHDv9EGnEzspxTGw48eaMTw+bjp+DLg9Ld0b93Uu7mj5myyq3F5UzNKpc6arbnBt+7m3HTUl23/fMV++2KLno4UhT7TqjtaQ6b9Yx49amx3TXGyCOVlJZKnymG2nDMTNyHHTlFOM1w5VnUcc+lBMl7TursDw0eXl68sYFrzl23swxw37bMTRL0kveUrkk6k9K0fAqZl6veFlGQ+issF6PeWn5ptuNcef+8bj0XUpmhvs5SUNbplwyW52d4ezUpWNi4bZmWfrlSbqZIhPswBlFrSLLOiuyX/tpKer8874kgFbJpIq/+ycfe16X28jmeK+Xen0gxSqKC5OIpbO9M51rL/OpK42c/VPnssmAs+9TOT95Ew1fH7uNm2is+VB8tyxfjvcydWmPNPTFWZr84Lnv4mUOE3dhen9XPus+xsGyUXLfZ1rKJpTmZMOlEdwXvuDu7LmltOUyHFteNrrh5e4jZ/6k8p0rlQzFw82V6mFTpvLcu5c2DxvqUNwZAAAAAAAADxMZP4My0hs618Fo2wPlkvHjomTJmRuHsxZ+kutypH6iZsj88Lr0oa5GeU5/12tUZdRarcbzssawlE7EqkqeTcgle8IZOYtuqbaEiR9bakR16e6Mn+w/w6RKC8fLkA3kJyfHR5djRqT1yHKZ3VCV1TRl6+SSXXb3z8fD5roabVlzXmbYXXzQ8VHnhUaecRpmszzj+UZpl1KpH9X6equla0Y1/jl5iIPyuiXL0LXKSvOfpb02nttlZrpWVZmFrL0jwKZTIcqlurnGnjEfp8NnSdKtob3wtu7lfJdr3XZc7Pg218yUa2QOGYT9kClWLpshw2hcYqk/rI0Xj3G2kItMY7UMx7TLqvrSLlS+Lx5T+jLlnDQqM7NKQ52wrmSe+vrcl9edsXHbWYcHjodFyrrtjQpKbIx938jPebWJTJIuMz+5qpKyRuW81ZVYcqZz6cb6/nIYc5fVOFNs6bzCxvWdlm6/5o6BPcfVrtuzvZR0W7EF98xZQa2zNZoq2qDFZukHDY0gVkjt7IjH+zN6ZhmZPs/N4/IJb6WdnLmhRekAl3NcVuOUwzTUPyz1WZ3N6tsbL8Vo/dxl6nXL9elmzjQrffTS66lcY6jr+e714JXap95v3X2IXBa+3I5Mvsl4Q9UyzhXbLuB9xpd73kSg8hKMDZ/fprlTX7nP7Gahd4Zp35dq4Y6fytEwLu/n8NyYS1pQ8oYs3t6gOmUbEHBGBQAAAAAAWFPrkfFzAqkNJXOj8nrlqirZPZVUlZnyMltaRv88FDlsgVzW91XDrNm4jCV7hLDy8OXZoV6QZ888+riVal3yexh71gOrp8yYj6qY4R67LkGpmdBopDqVWit+TtnNa5iI8ja2vqzTSCmX2/z6wwx9xM/EMVEfmcwaazTs8DVO27512EbjuB8Tb+ce2pwz3jr0MTl2PHM5Hf7eK01KTJRbHFc3nXVYdtGZul0Zp25Y414yMoajnkpW4dZdb3pYy1w3KsuZK2/xjvvkHuKmtDmVswonZRtSv1atVmO3Oalkd/mi9XbrGs5d3pK7qofZ1FKXRZXbKc+Kjhyv1dCeHc60Jm+7rMqZj8N5M3ZpSVXJBCLjZxWNU/l775RTyRQsx7fERdhwv+RMjnhISWrS3XXE5r5ebu99fixZ033JXE2N2hQ1Wkp9l9J+lXbrVleyaekHraqURupU6g46ftz25JGPeSmAOGSFSdmz6hO3D5vOtBj3EY+V+1N9qU/nWJxVnRZuj5YOzM7tYqvICGhH5TxXzp6lAhUerlKTJ4759rLV2Xkc13K56fqHB1H6R62zMJY+502bXm1pshxvjWuQtSq1Er17rjvJ5bLJhzVcNWTql/62+9WOOzJ+Hp52FjtNLpwimJdxLGY7sWvf9vla4y7ORduuAXXW/ZmDNh47LTV5XG+sblotSyz5a9HCNXRbP3ZUigpVJfM14mqZeyW3Q73vKzucNt6Ne8j4OSVO17sFAAAAAADAl209Mn5OYF1dvmN3JElalvWGG2MNhbpLNkZVdmt6RpKUvNtFydJIVatpyQ7qPSPm2izlF945K6NkcpT1qrM807iJUcxxKrteYFUlzzqMXduiHOc6pcPaUENNlYiPef+8n+0aLGX9cjXThuOw1DnwHLw2nBUyr8pa0jJT4Zn0tNBTVexu8VIuz8J9c4w2p9TUOfB2Odc8i7XRx/HaUsyAJ400GrI4ymxVxMXjOdYwLz3DMHGmRRrVyt5VsC/lw0pWoZ+7qLd9e6k35tmLfqFJ6/vy2a/8g+HLdy9ZqT6OS9fy2qviOC5KHZ1uU3Mf/FL2p0plJr1kU3gWy03TgVotOr+O26mys1vl1qcvNRRyydrxTjxaDtmKw5YYpf3yLiyd605htZSswGc8U5pzVu/d4ZZz1y9o3E74PLZo4/rM2VuLlIadTEtmRu/du5p8946WOUfM1rlkpXaSM0JyyQ4aMhHdbu3e8Ht1/bET+Nw4WWerbV2oohbH0n2W/bL7217ZDW4o9uOLrNnM7VTj3XH6y5Kkdyn6T1uu8zFJu5KkuvSnF5VyHXGRUszupyrqBNVuD+dXy25eZBmuJLcB7+imesem+z7V3TkIZ3d9DurcZ1JpKzpt7DgWXAs1O6MsOwN2p44sjBvziJ2rzgJRGusxx9euY2Om2H1ys4rvcsv2/z2Zz4hjW+5F5l7nGk1ldcOyf0WSdGH/Azrjfs0Zp6p7A0E9Po/rF8d372y8O5ae3o12ovL368bfoUrGYFn1M184a7rs1l0lacPnwGnE66yP7+bV5DlJUtudrgwxMn4AAAAAAADW1Hpk/JykMrNQdlzq8mHmRnlI2a2pn911Q+8RxD5lda7lk4YV62WqN37lyzzzzynrnkt2SNKkurv2C1bJ3UU6hmSdYbe25eEjh9n96q5nyjtYlF2Xhmyz3Ay7KqVh9r32Y2I0ui1xme/esWmkWssSmH7ssHPPV/4hcV/cvdtWybhJvl4Pc9p5GJEvNcDKjlwbfs7YM1aHcSf1zhjKw6vcHSN9SV0sNVrK7j1pNOxYWFUly5A94VZN2f2o7IhTZsTuvL+0C/1w/gntHY+R7sye6NSnu3dkGmp0DLulLH1/qTcmX46G16lLW1MySHxZ4jcTRyup1FLJ1WE8laywUrvlRn9LknQ9R6bFbcX1Rr1mqfRR4rLU2ViWmgve9WThHUq7oZtTqSnnylTqUcVzKtejmpyN2fjM/OTKStWm6u3I+Ckz6EObk8tOkT7flZodyrraX5Ukvak3JUnXFLG1512+5Ho9NxRZG/tD7aip5rnsbFlqUflrTB1Z12l0sby7E/mMOCmlvxPH63za1nbnjNSFj6FrsjSTiJ2Fj+F8ONXV6haRPZiau2tIte7XXGtv+TJi6mbvGKpmul7aJ2cRtnWpL1Z2T+V89bCVmm+d4jj3+YokaWf2WUnSufSRyBiVNPW5onHG2HhcavWWtqGs4Gm17zald7tUsqCr0t85cE3DttRXdb3CWhp1UXSqcbbrzOeu/bTjd3262hrOqAAAAAAAAGuKjB87nMUsu2+59k7XKeeyBrBMV3mUuC47qJTnekQ79cpef5yHOVHPopVq8q79U35uqafQpV5V2VWDVe0rqMwExJErO92U3bdKJsYyt3fsGFBmE1wLKpVMn1LTwDPpqbmj1lTcVzKADpPOSj2EUleq7JJSqSnZQOnu9a1YDWUmvU8x41APsxZx/0SlPkun2tkWdcn88mMnqexcEdfHntmoq07yTEYJ0VRqsgzxVWZcS1w4M6zqVbsmS+1dvQ6zxdgRblWUY7HwueWgisyfxrHRaH5YL6xkFZasoFKDxfWdhiyf1B3u6Na7vcqlvSrKuarc7vYltapTaYdKHPquksThn1t2AsNqKFGy6+N2uz9Q28etS7cbC8+KX9VtSdJNz8CWrIxGnTrv6lZis3EwHQw7WJYaT+5PlahKcb6TDjPLau/wVHv3lbQxveu9YpU426Le0K1JHL/ri5LZ4x1IXTtsPLQr8cxOvb7gWfwrOTJ/bjqLbMj4cUyUWixzX2/q/nDXuTJtXRodX+ZJ7ChI3Kym0qdt91sduI7YyId94q88s3ORnbHrLZi2vcPfNNfancfuTmp9Dis1xxx313LJ9LkpSdp3tuE8L3TTdVNz5Vp3I2eltXFZ6rzkTG26h2Xocw59hujnLLpoM/abF6QU2aC1dw+d1pE5tjGJdmnfjcNtv0TXLDTq4/mjNlqGuuw26PPefhfxspnLzrne4btP2ho9K0lqXEds6Uyxz88+E2/1lCXIk/EDAAAAAACwptYj4+cERtvKDHeZafeGE2rz4fy4emf6VJ5JPzLjUHmEsqqTUuUZ19o7oHgHn36otjAuT/ZbL9lCSSNnEh3W+Dllw4mnxT38WsvM5djZNRuerdzwMWuyhkwxDZk9ca0e1rG7fotnR+tRK/WlZkupt+HZkVRqCt1dL6hkFamWKsfhyHUbUsn8GeoOET8n5l7+JEuWRFWyxOJFSsZPl7sh62LI1qlKZoVrOvn2Se1MoFGn2jsoDTV+SmbikPnj2awhWy1urqtOU6+NHnvnL+YEVteBYl15qbWyX0d7cpD2NU6lRkHMkqXkTIsUmVzl/LP0OWxZN5p4B4xJV3YojNcoNROSMz/6oYZHyVzsNSkx7BnUOrm2kC+rsmPTsDUmVsmBzw2vNFd1tou//YN+6cs47m84zuYpYurAWWPLqh3iqtQHWvi477pdGpdsRtdTaB1DOR3WNsuOyVHJnnXfqSupaKnsCnUCHxgnxO3MaKzXvKPNi8uopSJn+tSjyNoox753RnKrTi+nyPS5nSK2dl1/Y881obYUNTXmjh9v/qVmlFXluzOlh+13SrZ+Pb3rPWJVHK5vkKSd/dvKS2d0LWLFQ+MdaW9tRu0neafB5G0q6z7pWvdi3OfdUZs+2qW5s3QaZybOnenTlHOeljpIT8XrlbgashfjOZXrjPVk/KyA/q7L3sdz1n1K0pOSpFEVx3OqyPxpfO6aHenD3O5nuta+JElKnb+Ttz7P+DvXzf4LkqQzjsHtUmsuV9pe3PBjo207WMZ7+eXFL8drnbKT03oM/JzEdu7ly7ELg039m2nzS8OyrMMttH3fQaSblY5wSXtX1WjmbQgrpyFWfUm9j9fY8nZ0WaWB8Rf8vNQv7cd72MlvntwHxL/snn6tTnX2l+reJ58Nd1b38uzw5JHTnU9RX5b5lesOqKbr1Lf+AtWXJWS+T2UpTjRGpTh4745SbmdlDFH7+XrcNmy/TPycuGP8SmsfoDJAU75Qz7rbvj+cyf2wdLAU3E0+4Xy2FE315dKdaXUzLVN0nltvp1vatJI6O/K2u70HBXoXPezznm7uxUnxoPmsn8NWuKumHMfby1clSa/qFyVJz00jfT31M+07tmbePns4wbsgdHmNti/t1Fy3vTXpzDHdDBnQXl5Rlu34NcoX9ip1SinSpzsvO8tOl276eI+d20Wsmjimt9uXJUk/fftjupijffAYnkbu71wYRVtzw8d21sfAY0qdbns75IV7RUu3YnOfv277NcogUuNzYp9qdVV0pssSrxKjY8fdtTe/4NsZNFw90Y68e/ucnr/k/m/twZv9Ujw1zj/X+2iLFp2L0muprrQpdcTHSLFkcNP94s+6K72bYjCyqSZ+jS31OeKwdl9rVHnSIsVg0WOb0Td6oSxvzZzLVknplz61sVQZrOs9mLfrM9bCa3R2m+gbzbpoc3ottPQAwI0u+rl7XtK19CTHE1UU995PZVDHfamqlurYAKMalQlVv6c+BrDbfu/kPiiO6WiBbQ8Y5xckSbvthnbzpyRJO+kJSdLe6F2SpPfP43LpuLpRNjipW11ybF1tIm522vh+vcxxzJ9w23PNmxkMm6PkShMXnz9wX/2Gl6i+soj3dNomtpjWBQAAAAAAWFPrkfFzIjy618XsxNiXk64elmmpL6mlTjvUhp+79HUXKqsbjYbivDFSPc8eRXTqWZMe9/VStDVmNEaSRk45a1ykDKunzJx3zp5YOstm0V+TJKW8OWzJXnZZL8vDSrbX4bbuLnKZD5Sdetr6vtZZG8tSiNezsq1K1ohfO+Vhxr7Nr/tWCqqukpK982L/aUlS7WO6qZihelzPSJI2Uj9sfduU2Y6SqeE0sf2ypMLxcqADJc94JsdkdtZHWerXuTjeMIPu1+q11HK548e85ndLltiqGTJ+PNv08eYnJUkHPt7KSUtnVJTtsyde3jf2jHo/LK+J2fCZOu0rZjsXvq3zZe9lWlkuiDlsNuDZemV1Zctmb5276F6RJM3bX/AjiaNVVI5LiZO/t/9PdEYxG167uOWGl3E9U79PkjRT2ZK9LPUb6ba34+5KdoXjrfH1xbC8x1vzDhtXjA7PoT5BNj5d7S0jnqud6Aex7GIVxbnj5Z3P6RffiNn3pw7iXHR75jbIGwYsnO1V+s1V6vWGt0E+cFx0w+YnLjDuStALz9x3jsW2ysPr5CFj2tlmjrWl+2D0f1ZTKafxhb1XNGndF/ZavvI96Hrvfk2OrOSyJKvTQvvObN5NXtJVlWxC95XdrylLvfrhfDXSSNGmJH+X69p4jd3mjZP9kLgHR/sMZamXYyC/ocp9lsrtQlVFnMyrUhw+LurSxx1lvebvVLe8RHDuBqTJJVs1YqHEWhqWkkpZ8fo3l6/5NeK8N2tv38sHfWjI+AEAAAAAAFhTZPwUpWBcH6PEU2f8jPKGctlLu2yX7QwNVaWIXIw4j3xZ5blGHj1cuE7PQR+ztI1HHW+rPDeMPHJZp7FuzGIUcdGfztHER0OpexGx0HrL297FCjfy7WGmoWypXK5fSGVm/cDPLbGyp7kLt7Zed9p4ffxhwd67Z+5LMbpaU3VesDzrX77rMVgNpbDutez6J17rvp0vSZJupcga29BUKZXZiHhM6xja8mvMnOVx0zG0mw9U5ZixT0OmT8RQKfKcO2+PPBTHdBaZkpaOs7ajrtiqW7oWymv9r0uSbi1jhnsrnVeX795EoGRvjBTtxJeJhEcAACAASURBVLC9ey5tUFaVN/z/8djWmWiHhXgv+ieXbA0N19vOmWk5ZsLa3peuw4HVtnSf5aX2s6p9/JNKLcOIgzddBT75/kkV56BRtaGZ+zc5lbp1LtLq12+rEjMlK+0whnKO81TbxTlz6ezoUsNld3nTjz1d9RMeDdEK3Ji9rp9946clSRe7yKbYnXvWffP9fmzEz8RFl1PVa38Ux7Tp7z7PtKW2XC71WcpGKqWfdaDWP6fry/nNmQCOo84/n9o+qyaO9cw1eX7m5j/WJEcNp5Fr7IxTtC3V+LIkadmXunLRbszzvvI44mjuNqcUhJ45s2xROXOjL3XtvPqiz6pcqL53vanGbc7+smTJ4+HLR67FsV+WPkXfqRq+P/t4NnEeqof9ALzRjductm1Vb8VqiQN3gVrXBlu07sOM3CfqI55SySDs9rXsIiPsdhv9m3lX6mOeznMTGT8AAAAAAABrioyfI2qP8m16XXndJdW5bEcZo3vdUJsl6hokry1Nnn1XWmimmIVd5ricebSyZPz0R8bcquzZ91QPWUcdGRsrrFSeL1lgpQ6Ba0NpcbhrV6lzkMpW7c7qKRk/ztDo0sGwY0HjWaxSs+OwNkLJ0vC7cNxU1VitJ7ga77rCGvdV4/oFzti42UfNnZljZuYtbTfSGVU+wmXGs/Ox3HJb0zje9vxacy2VszN6yrbu5dIzn/lIm9Onso9YUu9dwzqvrcfqKjNgZYekXdf8maUdHd0Ro9QVK1kcLo9xmEEoaTrMnjnDZ8gGiudWOu/b73yWpNxr6RoM7ZCtMfMjOHedJm1eDHXl0uHZRZJ0xdsnj6qYnZ+k2Dq3zptq3ScqmT7JGWatdzMtOy7loc9UdvFptOxe8mNv+raS3erX7Mg6XHXLbl+v7P2KJOmNHMez6eJYb47j2Nd1ZHNMctQKU+7UlUywcln6SF2cA1PJoHa8ZG992natFk3ZMdBtjnenzM7waJclfomfVVTamRfmP6ORzz0lgyM5M/VS+rCkw/NI6UMf5Fva3oiaY0421bKLGDpw7FTlOW5HSmZ12x9IrsnSlYwyZ40d9nuImdVTajS579vvKLlOVOdjvvCKmtTEOSo5G6waas4tdebMN8RzpqVepjPQOvdZvJV3KenbNnH7bHlVTRt99YV/3mGmz+mMFzJ+AAAAAAAA1lQ6nMV7AD8spZUfHttIUSfjfeNvliRd1Nawq1fZCaVOXjd4pPp37VmvWVrqU83Pxf/3ZYS5zHiVLIwyK1GuHV7POjKzegrknNOXftTxrHLcVE6aO189KUn6qulvliQtu7mWw+y3H+vR5yvdZyRJjbM1ShbYMs+H3bryUAvhaNZOuuO/8Q4kKaX0Fs9Z2V/b4H7GjbTasVOOYqmtUZcdmNKWhmOXykVZH+/ZzXx0HXQe6gIdxsHRduTL+VWv8K/riEe1zXl76Y7/u/tXc3R3raP33/38uy9TyQw70r7c3TadnnPWo93mfPkOs8WiX1POX9M6apJtT9+pZVtm1Uvmj2v9VHFZsjLKzGxfspnzbNgRrmQBnYYMVdqct+LzmPvFlS9H42fjumtCTafviMvJE+rcliy7yPbqHBclO7VbXPHtruPTl7o98yGGcj4aN6v766PNeStpyEQdV5ENNk7OCvPOt6XNGY8i63Q03tasLTsElkzmUm/Tqyka95HK6ory3SsvlPuh+pgfc/dOlauINuftDfXoUjlHRdykyrtkTyI7dbx1SaPpeyRJTYkPf//qnSlY+7WaRWQPtUu3Qe3u8JhVjpOjvljckPEDAAAAAACwpsj4OaJ2DZUn6uclSU/r8WGnlOUwSux6CR5RVllT6hn3uRq90Xu9cxlVPAWzWffiUR2VLrOiY480X6hiVmtDIy187JdDtlc8dqlSF6PUeyprkvMdNYO+0o+cdJpGowtmwqQyY1qV7C1VKsfy6Js/jI8v5hR85BPwqLY599/RX+vb1cw4nb8i2pyvTBrmB+OyzMLXaVPJ/aVhVv1oTKQyG3+03liv05DhcxRtzhdTMsQcJ87iKBlAdR27A47qiyrlRdsh46fMwnsHyiFe5nffrk6nKbuwoM354tLQ97k7g+Mw63Q0XB4effeFjma6l92Xh12Y78zqWf3ssKNoc74cd9cyHFZCOPO0qqaqR09JknJfzlUlPuKcVH4T/bBjV8ks7LRu5yoyfgAAAAAAANYUGT9HDBkcip0ILqTz6j2i3AwZP2V08c7Zq8jYKJcL1/95VHbmetRHpdOQteE1yRqpO7Ij06G7a7B85dk964OZMBzXo97m4Hhoc47rreoSlrnDo+eysqtc5Wunb6b9rdDmfCXuzGC9I2tDY6VUMsVKZs/RjLFySdx8OdYvdt7u1/VWt7/dR1+PXwltzr24o+5hySLLb3euKjuitnfdflp9sbhh4OdtlJPV2F/kpcOBncNSqUeLqGq4v39EBnwKGqe7paEcr3TaG5D7iQ4Rjos2B8dBm4Pjos25F3cWjS//vx4DO18KbQ6OizbnpLzdkvX1xFIvAAAAAACAR9DoYb+BVVVSk5da3rH1bbrrvrffJvnRGFHE23uUl28BAAAcOn1FmQGsC9qdgowfAAAAAACANUXGz5eUv4zsDUYSAQAAAADA6iHjBwAAAAAAYE0x8AMAAAAAALCmGPgBAAAAAABYUwz8AAAAAAAArCkGfgAAAAAAANYUAz8AAAAAAABrioEfAAAAAACANcXADwAAAAAAwJpi4AcAAAAAAGBNMfADAAAAAACwphj4AQAAAAAAWFMM/AAAAAAAAKwpBn4AAAAAAADWFAM/AAAAAAAAa4qBHwAAAAAAgDXFwA8AAAAAAMCaYuAHAAAAAABgTTHwAwAAAAAAsKYY+AEAAAAAAFhTDPwAAAAAAACsKQZ+AAAAAAAA1hQDPwAAAAAAAGuKgR8AAAAAAIA1xcAPAAAAAADAmmLgBwAAAAAAYE0x8AMAAAAAALCmGPgBAAAAAABYUynn/LDfAwAAAAAAAO4DMn4AAAAAAADWFAM/AAAAAAAAa4qBHwAAAAAAgDXFwA8AAAAAAMCaYuAHAAAAAABgTTHwAwAAAAAAsKYY+AEAAAAAAFhTDPwAAAAAAACsKQZ+AAAAAAAA1hQDPwAAAAAAAGuKgR8AAAAAAIA1xcAPAAAAAADAmmLgBwAAAAAAYE0x8AMAAAAAALCmGPgBAAAAAABYUwz8AAAAAAAArCkGfgAAAAAAANYUAz8AAAAAAABrioEfAAAAAACANcXADwAAAAAAwJpi4AcAAAAAAGBNMfADAAAAAACwphj4AQAAAAAAWFMM/AAAAAAAAKwpBn4AAAAAAADWFAM/AAAAAAAAa4qBHwAAAAAAgDXFwA8AAAAAAMCaYuAHAAAAAABgTTHwAwAAAAAAsKYY+AEAAAAAAFhTDPwAAAAAAACsKQZ+AAAAAAAA1hQDPwAAAAAAAGuKgR8AAAAAAIA1xcAPAAAAAADAmmLgBwAAAAAAYE0x8AMAAAAAALCmGPgBAAAAAABYUwz8AAAAAAAArCkGfgAAAAAAANYUAz8AAAAAAABrioEfAAAAAACANcXADwAAAAAAwJpi4AcAAAAAAGBNMfADAAAAAACwphj4AQAAAAAAWFMM/AAAAAAAAKwpBn4AAAAAAADWFAM/AAAAAAAAa4qBHwAAAAAAgDXFwA8AAAAAAMCaYuAHAAAAAABgTTHwAwAAAAAAsKYY+AEAAAAAAFhTDPwAAAAAAACsKQZ+AAAAAAAA1hQDPwAAAAAAAGuKgR8AAAAAAIA1xcAPAAAAAADAmmLgBwAAAAAAYE0x8AMAAAAAALCmGPgBAAAAAABYUwz8AAAAAAAArCkGfgAAAAAAANYUAz8AAAAAAABrioEfAAAAAACANcXADwAAAAAAwJpi4AcAAAAAAGBNMfADAAAAAACwphj4AQAAAAAAWFOP3MBPSulXU0ofPcbzXkwp/Y4Teg/fklK6nVL6WErpkymlz6SUzq/aa+JuxA6Og7jBcRE7OA7iBsdB3OC4iB0cB3Hz4K3lwI8DYpZS2kspXUkp/WhK6Ywk5Zy/Nuf8sTsedyKB8xbv4QdSSh9PKS1SSj965305538m6Zdz/v/bu/MY27LrPOzfPsOdan5Dz81udpMUKZISKbZB2dFkWbFsIspkJ1ESK3GAAIEFG0icwBmgPyxHjmwjie1IlmUHjiRbRiQrIQTFdhTHDpKIFqyBiky1JPbAnt881HDrDmfYe+eP9e1b9aoHNqtfdd069f2A1/fdsW69u3qfc/dee634HQB+GsB/GmPcfS8/7yRe8zw67dhxzvWdc3/LOfeqc27snPtN59wfTvcrdpbTaccNX/unnXPXnHN7PMj8h+k+xc3yWobYOfRePuycmzvnfjrdpthZTssQNzypnfM97Dvnnkv3KW6W0zLEDV//e/mFaOKc+4pz7lv5HhQ3S2oZYufQWJP+eOfcj/A9KHaW0JLEzZPOuX/onNt2zl13zv2oc67gezhXcdPJiR/6nhjjKoBvAvAMgB94n3/+VQA/BOB/OnqHc+5R3g8A3wjgS+/1h53Ea55jpxk7BYDXAXw7gA3+7L/nnHsSUOwsudMec34YwJMxxnUA/zKAH3LOfQZQ3JwBpx07yV8D8GuHb1DsLLVliJs/GWNc5Z+vSzcqbpbaqcaNc+5fBPAXAfwHANYAfBuAl3if4ma5nWrsHBprVgE8BGAG4OcAxc6SO+1j1Y8BuAngYQCfgn3H+n7g/MVNlyd+AAAxxisA/ncAnwAOZhSdc38HwAcA/G+chfwzvP9x59znnXO3nHN3nHM/eujlPuWc+5Kz9K2fdc4N3uHnfj7G+PMA7rzF3Z8E8Cz//oEY46v34Vc9idc8104jdmKMkxjjn40xvhJjDDHGvw/gZQCf4UMUO0vuFMec344xVukq/zzN64qbM+C0Yoev9b0AdgD8kyN3KXaW3GnGzTtQ3Cy5U4ybHwTw52KM/4znOVf4XgDFzZmwJGPOH4F9mf8lXlfsLLlTjJsPAvh7McZ5jPE6gF8E8HHed67ipvMTP865xwF8DsD/d/j2GOP3AXgNnIWMMf4l51wO4O8DeBXAkwAeBfAzh572bwL4Q7AA+gYAf/zQz/kx59yPvcu3dTgg+o6r8u/RSbzmubYMseOcexDARwD8Nm9S7Cy504wb3jYF8GUA1wD8Q96luDkDTit2nHPrAP4cgD/9Fm9LsbPkTvlY9cPOudvOuX/q7q3VoLhZcqcRN3ydZwBcds696Jx7w9m2iyEfrrg5A5bh/BjAvw/gb8cYI68rdpbcKcbNXwHwvc65kbNsnD8Mm/wBzlvcxBg79wfAKwD2YauXr8JSvIaH7vuuo3/n9d8L4BaA4m1e848duv6XAPz4u3gvPwTgJ0/730R/zmTslAD+MYC/cdr/LvpzpuImB/AtsFTa8rT/bfRn+WMHwF8F8J/z738WwE+f9r+L/pyJuPksbKtOH/YlbAzg6dP+t9Gf5Y0bAI/AslF/Hbbt4hKAfwrgz5/2v43+LHfsHHneEwA8gA+e9r+L/ix/3AD4GIAvAmg5/vwkAHfa/zan8afLGT//aoxxM8b4RIzx+2OMs3fxnMcBvBpjbN/m/uuH/j4FsPqe3+U7cFY4Mb7Nny+c5M8+5049dpxzGYC/A6AG8CffzZs+8nzFzvvv1OMGAGKMPsb4BQCPAfgT7+I9LChuTs2pxY5z7lMAvgvAX/6a3vGbX0ex8/471TEnxvgrMcZxjLGKMf4U7Av85971u4fi5pScZtykn/UjMcZrMcbbAP57KG7OiqU4zwHwfQC+EGN8+V089h6KnVNxmuc4GSy75/MAVmCTzVuwOmPvWlfipjjtN3DK4pHrrwP4gHOueIdAe8+cc0d/7sEbitEd+vt33I/XPPq6cl+cWOw45xyAvwXgQQCfizE2h+5T7Jxt7+eYU4A1fhQ3nXBSsfMdsDTq12zowSqA3Dn39THGb1LsnHnv55gTAThAY04HnEjcxBi3nXNvHHn9xd8VN53wfow5/x6Av3D4BsXOmXdScXMBVj/oR6PVwayccz8B25HzZ85b3HQ54+fduAHgqUPXfxVWF+MvOOdWnHMD59y/cJwXds4VzgpN5bCT6IFj6zje9lMAvgBbIftYjNG9x0D4LIB/Bity9jMAeuk1NTCdiBOLHQB/HZaW+D1vMSuu2DnbTiRunHMPOGuPu+qcy51z3w3g38ZBoV7Fzdl3UmPO34RNEH6Kf34cwD8A8N28X7Fztp3UmLPpnPvudG7jnPt3Yd2ZUt0Exc3ZdpLnOD8B4E/xuLUF4D+B1fIAFDddcJKxA+fc74PVe/m5I3cpds62E4kbZhW+DOBP8Fi1CduanDptnau4Oe8TPz8M4AecczvOuf8sxugBfA+AD8GKTL0B4N96Ny/knPtx59yPH7rpB2Aprf8FgD/Gv6f2dZ8C0I8xfiuA/xJvXVDza/U6gO+MMX4bbO/jv3IfXlPe3onEjnPuCQD/ESxGrjurbr/Pk2pAsXPWndSYE2Hbut4AsA3gvwXwH8cYf4H3K27OvhOJnRjjNMZ4Pf2B7cWfxxhv8eGKnbPtpMacErZiegvAbQB/CpbO/zzvV9ycbSd5fvxfA/g1AM8D+F1Yodc/z/sUN2ffScYOYF/aPx9jHB+5XbFztp1k3PzrsELQtwC8CKCBTTgD5yxuXIzvmI0kJ8A59wCA/wG2Iv89AL45xvhf3cfX/0EA/zzG+Pn79ZqyHBQ7chyKGzkuxY4ch+JGjkNxI8el2JHjOG9xc95r/JyW27DZxi8DGAA4dsrjUcwY+YOwlTjpHsWOHIfiRo5LsSPHobiR41DcyHEpduQ4zlXcnPetXqflDwJoY4xfB+CPAPjv7seLOufWYZ2g/vjhgsDSKYodOQ7FjRyXYkeOQ3Ejx6G4keNS7MhxnKu40cTP6XAA7vDvtwFsvOcXtMLRPwPgB2OMz73X15OlpdiR41DcyHEpduQ4FDdyHIobOS7FjhzHuYob1fg5BQyIvwvgIQB9AH86xvjL7/E1vw/AXwHwW7zpr8cYf/Y9vVFZOoodOQ7FjRyXYkeOQ3Ejx6G4keNS7MhxnLe40cSPiIiIiIiIiEhHaauXiIiIiIiIiEhHva9dvZxzSi/qqBijO6nXVtx010nGDaDY6TKNOXIcGnPkuDTmyHFozJHj0pgjx/FOcaOMHxERERERERGRjtLEj4iIiIiIiIhIR2niR0RERERERESkozTxIyIiIiIiIiLSUZr4ERERERERERHpKE38iIiIiIiIiIh0lCZ+REREREREREQ6ShM/IiIiIiIiIiIdpYkfEREREREREZGO0sSPiIiIiIiIiEhHaeJHRERERERERKSjNPEjIiIiIiIiItJRmvgREREREREREekoTfyIiIiIiIiIiHSUJn5ERERERERERDpKEz8iIiIiIiIiIh2liR8RERERERERkY7SxI+IiIiIiIiISEdp4kdEREREREREpKM08SMiIiIiIiIi0lGa+BERERERERER6ShN/IiIiIiIiIiIdJQmfkREREREREREOkoTPyIiIiIiIiIiHaWJHxERERERERGRjtLEj4iIiIiIiIhIR2niR0RERERERESkozTxIyIiIiIiIiLSUZr4ERERERERERHpKE38iIiIiIiIiIh0lCZ+REREREREREQ6ShM/IiIiIiIiIiIdpYkfEREREREREZGO0sSPiIiIiIiIiEhHaeJHRERERERERKSjNPEjIiIiIiIiItJRmvgREREREREREekoTfyIiIiIiIiIiHRUcdpvQERERERERM47x8t4qu9Cll0OAHCuZ9eKEQDAt2MAQIwNH6c4OkwZPyIiIiIiIiIiHaWMH3JH/pbx0sEhcwd/B4DC2T9bLysBACGzWcd59ACApp0DnIGMsNtibO3lYzjyEz0vNSN5lqXYyHFvrAAHn+zRGIu8ISweF3EwF+vuee7B33i5iKMAOdtSXBSLz/5gPj6mz5tjUODnnm6/d9RweGtHxxaNNV2QxppVZ8ch5wrEaJ9txeNKipcWR+NGMXCepfObEWMnczkCY6LiuYpn7ISjxx4597LFeXKOgBQnOheRr02+OHbZ9yU4O/dJmRttY5kbPsz5jAiNQ1KU6wCAwfqnAADDC8/Y9QsfBQBMt98AAMzu/DYAoJm+CF+9CgCIccbL6v17w0tGGT8iIiIiIiIiIh117jN+SmbrPDrYAAA81N8CADy1/hAA4OFsA6u9VXtwbwAA8IXNUhcrQwDAdMNmp19opgCA33juWUxgz2+CzS621e49l0Vur+mbq7z9Fq9PEGPKApJllXNl4mJhMXE5t1j4cH8TALDZexgx2MrEnreZ5crZ5+oZc7PSXmOv5OPQ4nZmKx9u/SIAIPa4Z7Wx55abfQBAe/01u/2OxY+f7KCubHUEip+llrLB1nIbRy7mFkMfY+xcHj2NEOwzvN3uAwAmwWJoN9gYM441AGAftjpfu4gqt7iKpcWiZxj4yp5brvH2XRtrQs2Vj+AR40HemSynlM+1ldsY8PHS4uUPrD0JAHji0jMIrX3oz+/aitcLs+t22WwDAHa52jWOtoJaR4+Zt5ha5HUciQXHsS6GozGiWDkrUuysMEv5qd4aAOA7LzwBAPjw5Y9jbzYBAPzyrZcBAC/ObZy4xbFn5hkzweomRES0KZM5iUdigrEDjS9nWsrw6Ts7xjzSt/PlT659A96Y3QAAfHlq5yQznvNGZqnGI1mq4LWv9hONsoi6Jp3/lPkAG6uP2t9L+77ko30l3Xr80wCAO9d+FwCwt/M7AIDgJ2ja7SOvqBg5T1xWYnTRMnsuffhfAgBsPmHx4tYsnhpvMdFMbSya376Bnd/+fwAAvraYmtz5f+16u/c+vfPloYwfEREREREREZGOOrcZPxnnvEpYhsVasBWMj+NpAMDvKT4OAPjQ8BGslrY6lpeWpRPWLQtjvm+rXbtT+2d8etNW1B965rvxK9uXAADbM7uv5j91zG2228NWYtttWyWpb/8KAKDa/SXU8xf5LjWTvWxyxs16bjHxRG6f8ydyW7H4TO+DAIBPPvh1WCtX7DmFXfoNZorduQIA2Fmx1fnXH7MYfOkj6/ifLzwJALg7ssyz+oJl/hSb9hrDfcsA8bds1TXftsyP7OoubvzU99tztp/nu9Xq6jJJY85WaWPNE7ldfpSXn+4/AAD4vY9+Kzb6KXYsGyissXvBzRcAANMV+2yvP2TjyktPrOB/HF4AANyIlglSXXjcfvBjFpsrr98EADTXGENvMPPnlZew/5t/026bXrtfv67cJ2m1faOw488HMxsbPuQeBABcaB4BAHy2/wmM1m3v+x94wOKmXrW4Ke/acWa/Z1kbb1y08eO1j6zgr/m7AIBrLLMwf8Dix334A3bDF58DALQv2zErvmZZhuHKFVRf+Q17TKjvzy8rJ2KVGalPFvbZPlPYmPDR+CQA4NtWnsDggj3m33jyWwAA1ZpllrnajidjZ5lhb4zsvOcrWwP8xS/Yffu7rAvU2mvE7BKfa9kgYe8Vu53XY5gBOJItJEvnoBaUxcIne48BAP7Q1u8BAHz7Bz6KorSxZi/Y8e2at1X2F678AgDgufkdAMDrsMyx23nA1bGNFy1X5mNmcQNmMWbexic/4/GIWUQ6Jz7LmOmTWbw8sfUMLmx8MwBga+P3AQBG6xZf6337jrXds3OVO6t2rnJ38hxe2/tZAMC8+goAoPUpA0ix0W0ci/pfjyJYvEyvPgUAaPftvOfCJ+37UmgZa561V8vLeOqPfgMAYP81+3797D96BQAwGT/7Prz35XJuJ36OFrkMwU5CZo0dnMYzO8kZrozQgw1CWeS2G28HKZfZwclFfikLPFFqM/Qv28n5YMY2cyxiFlKt1hEnkTaY4sgUtcnrW7h79UfsvZ3j4lPLywaSHr/Ej5iamgaYwC1ZG24FoxQ3sC/xrbfHFtzS05b2+a4VFj9DFBg8dZmPsYHMr9sEUxhabOUDe42sZwe53kULqGJ1A9mKxRK2X+B71cTPMknbA1NB1QuwE6C1YNcHrcXBFkZYjZz4cRxz2LayGNmX/eGKff5u1eJu3u/hkc/aZPXcWeyM1+wgiHUbay48ZBNMcWZxkc9szItvPIMXXvo/7edMb/Dd6iRqWeT87FfArYGMm3WOPT1+fx6GEv3AraKMm5yNCPrcupz17QvUA5z4qS8N8Onfb4UR+0N77Pa6xV5ctbFn8zOfseutxUTOrYP+xl385uf+KAAgjK/fr19X7qPFQgW3eD3OL9gPMpZGtR2vhi5HP7NjDHjsKUcWQ8Ovs89/vbQv62sbNn5sbvTwHd/17wAAXti2uNtueazL7Lnlq/bFrb5i28iaV1636y//Osav/mW+S00ALas+x48nCjt2fCO35DzOyecHNh5Hb9XOZy717ThzkceOb/6WDwMAdrnN9AbHnueyCX5+YJPV1xqLl+qSXY+XbfGieN4mo6f/nAujL34JANDe+E1Ud/4vvjttaT9LShZwfnjFtpdeWHsalzZty876mk349Id2znLxMTv2bFy2xbBHxvac8f7H8NDgswCAm7dtS+rVl38eALBz5x8DAIJnyQOdw3RKkdsxpeg9hLywuIjBzoXamR3n0gJEavNeFjZ+OVdgVvN8lyUWelxonY65lf0cxYu2eomIiIiIiIiIdNS5z/hJRQc9ixROmKa6x8KnTcyQpUlELjA0nC4bsx/3mCv5e1O7vt8C8779vfUsuMqVk5QRX64wS6hns4/lOh+3/k3Yvm4rb9Er42fZpNa2BT/7fkxtTZlBxtTlMubI2tSvnffN2VqZmR11bfdPxxZg+3cr1JnFUptxS+CijTcz0zLOYDO+WM8X+SgCgwt8l2/X1ltOU6p72o/2GQ8ZOwXvcK1d9jxQ8O8uZSTOOfjMOWQ7G0j8tsVOU0bUecSgHAAAIABJREFUha2oea7cx5JZhqnAas9uLwpmHq0zloveQbaYYmdprbCw6nrK/uK44lh02fkGaHmwyrl6VdtjmoqXjLX5xOJput9gtsKtqKOSP8hW1mKfWYZphYxj0QbfT7a2gS9dsrgJ45QppizDZZL+b97k+cdFrvX1meGM1s5zQlMhcFupY+hEbt2Zb1u8NQMbX+YcP+ZlH9mHLFOjt2KxMnBcgWVG0crQMkMy2wGN4tO2lb55/hvx7N/4Sfs57a378JvK/bQoJM9jydO5ZYFdZGmErLbjz3zcwqX1Y2Z5ZYyPJjIzvmdZzCsbjq85x0XGwdzZY+bcyh44Bo2etLhqP/sxe82db7frL97Gl/+bz9lja2UZngUlx55NFpR/ZI3nGuUWWmY2Vy3PWWr7/K9PeYzjborBiOfbeQ+jyxYzDz9guySKDcsG8r9hGRyTvV+067WVVIjQNuSzzDF+hkP7fIveA4jMem6ZsRpaNju5vc9n2ThV5syA9nPMG7svbtu5Sl2lx6bR7vwUlFfGj4iIiIiIiIhIR53bjJ8ktRaMMdX8MSnToi5LBGZocBEeNScE99l6e8J/xqm32erGAy3rZ6BKmUV8YdbX4NZEuNrm3jLPGcpiCxlXWIO2MC8hZmVw9b3g3GnBVfgsFfEuSnhv9wVmAVWLz9M+/DljbspV+nlVoOFKfHpOKHiZVvfbFC/M+OFr5iEDept8fWVtLCfGDmMmWwwNaQzKFo/zjInIVsoNV1GLxuKs4vg0G1t8THoR45u2el+z2GbbWh2X0NjYUs/tuTnjrsfRv2wyoFi/X7+knJAhV75KZnA5ZoxFxlPrPPLUartl3HB8CMw2nPKgsjux+Nrbz3DtrsXNjrf7ZikwCjsObdepKKf9HM9sxBEAd5FZhi+nMUcZP8skfRqrzBRNWVupDXvFy3msET1Xxhk7NWsZTq6xjfvAXm27ste61vTw8sss2MuxZV6yWG/J8ymrJ49iUSTYYqq/tYZ8yKyO8e0j71ZOn31el3I7lmzyXDdGGyMmrdVs2tmfofYWH45jz2xoz7n+WzauMFwwu2CvcWXYw7UH7fW3+XOaOX8sD0OB504u1cXbZLbjR3PkW1YXJtxgcJ2DFfqzKNU0XOP5yGbPakD1Mma8uz4qZqQ6phl6b9cnt+16n6+xwmNPjhw3Xuc4wTENwQrJj9asKL3rZXyNfwQAaJtXAQAxtlCsnD0Fsw5HA8sczMoLaFnfMPI8ObBwfNyx+k6O37FS/Tjn91FPrMh8nNi44ZspH3P+vi8p40dEREREREREpKPObcZPmuPznAGunM0M1kyhmPXt8qXdqyh6tgzR8rLJbWXjbm0ddva4sj7P2Vq7rNFnfRc/taWMLNpjUn2NnanNYoYpZypZz8cVfYRGe1KXVWpvmjNuSq5UlCl9gxk612c3UfRtxdSzNfeUNVZadj4ZjxgLtvUZTa9F1qZq9BZ/bp0xtWmPnV1l5xXHmh18H71RBKbpf2etnC6j1GFnNe15z+2zXOfqRGrdftdXGKwx64972+tV1l+5YJfzda6YbjKbZz1gtG6vt8bV0d5Frm6tsobUHXaEYwzXzPwZFA75kEU4zuHqx7JLWYUr4MoXO3aVzsaROdvjXqk9BmvMMhwxC7XHTMTHbbVsf8XGk9ubdnlnvUazYjHlNuw5+YrFAMu1YFIyQ41Zjm3Khh0MUH7m9wMAmi9+wR4cdexaJjn/f15jzYPVjN0CYavv49yuf7HqoxjabfXQDkjTgcXZ7OEn7XJk48l4xY5Ne/0W9SqLzK2yU2CfmYocruYPs24QM1RbHpsGsyGywUfsQePf4rvVcWtZpGPEBtu4jzKLjQjLKt7l5bOzFWTgeQ7rOk2Y/dWufwgAMOY59ZTph+NyDjfl4MKxJh2jwC6lUx4TYypFxTDzoUB26Zvsys1ftkuNOcuJ/zuHwFqGsHpfMVimX7X3EGpmc8z43anXsyyxJ9g1rmImWCpZ5/KA0SUbs3Z32JmSMVL2P2F/edQygLx7GAAwv/MP7Hr9HEJIrd811pwVOY9Zg8xat4f4BGLLWqfRsnYcs5DrGTvZ8vs8hy/kowBUzC7csdo+nt+zDyLh/GyxUcaPiIiIiIiIiEhHnduMn3jksuEc2DZveIP1DvplH1luKxoxt1UPz8vbXDXb57JEG2xZYuIb9NZsqrGxrdBwbNDlpjZ1vbLJ+gzBPoIBV3Nj7MOlaco4fs+/p9xfi7jh3uOKl3d5z9DbKsRq3kOZWdwEZ3EyCan2ivXF2ZvajPP2nj33JhoUE/vsU62gvM+5Wdb4Ke9yTzTjacCV1HIbyLjHXlkbS46ZE3PW9NlJscPuTNeyAYbsdhGCrb7Pa1uxr+ZcIWtszNlmV4Ob0wA3tnhDayuvMdWAmdjrFjspW830eFmOgbCbujLJ0mGGTc648Rxz9tmRssf/71/PMqxw1T0Gi5Mp6zv5HRt7JlO7vsO4udO2GEyYQTRgB8EhTwsYKKnLU+og2OPqWuYjwmtX+Sa1grqc+JmyHsY0xRA/04rHlavBoWCdwRiY+ePtODXes/hoqtSplCuno4is4vGK3XgKdh1Mx8f0c3Ku+g9Ku+ztB8RFYRdZNoval6w3WbHGzzY7vc0YN9d9jpxjTFYMeR+z2Wu7rHPWe7JDGppZH9k2z2/mPFdZXwwu9tzUvDJ1T2UGWa8BUKfzHFlmOevyrJT2wQ8LG08cv+tUWbXoTtpPGRqsIbU953XunEg1fgrn0DQ2qPAwhBV2G3Qtv59tWvZy+ZCdO80y6yJW7f0axrs/AUCdvs6C1C1wWLAroLOuXtOmReD383Qum6U6h/M9ey6DIw89Xs7RznYAAGWqccmsMu85Xi3qP3W/DpQyfkREREREREREOurcZvwscGUqcEVjn/US7jDrxveGQGErXq7HYixlyvThajxXOyNXK2rXYMCaL2nFK2N3rzixmeb1gb2+4+z1Kmu2VHVAv7Q9qtPqDt+kVlOXjctsCarlHuUxV9rvsH5L2x+hLCw+Qm4rHRX3wjvHehvMFNtjx50d16B/g/VZWAuqnfCzX7UZ7nKPqx1cKVthgOU3GhRp+psZAgqb5cLFS2Qcaxpnl3vBYmfIHJznyzUM2GUrZBY783hvBkcac8apS1PVoH/bxqle6gq4z9V9xkWfY1DqCDeMKYvMw8137t8vKieixxpQkSumU586Ndnn/eWyj1F2kDkKAFXD59Rc/Zwzbtiacn/eYvi6PWaQmlykjhmp0RtTwwqeLaxwBb+oWmBv7779fnL/pbXLyHpiE8bHhEV45hyDXiv6KHi8ynu2Ero4bjHzJxVaiTOuF/qIHuvK9Sc5fx4vq/SD7YKl77CWai7cjcgW67XKUF026dShLewD22c2z4TjSR92rLmFHCVX1XspoznaZdkw+zBlazTMFJsUKG4y86vHzKJ0yfHJr9lxLeNBc9RnZvN+Cxe7vyLfBT2ONat9q7tSltYBMsDGmTqfwsG2RBSFfS8KrJ+601itn5KpX467KfLgUc9T4aeUDcbYSV0ng8VmMWRds4t2ve49iOnk/7Cntq/xXSqWllXO+FnJHwUA9HgcCt6j8Cnri7XlUn2e1s5jHTNb+xyLECbs6gaUrFdW5FZrKjAWPMe0Nu7a7TicWXi0a+nZ/nKljB8RERERERERkY469xk/aWYwZfzUXBnbZ12f+WAA5DYTmPXuvWxLXqaVfGb8eLQYFTZb2OeiFrcow3Omcr2xJbGitZnKNWePn7YVVgaWETKrXgAAxHNUbXz5seNNzswLZv6kVfIi7YXvDVBkFh+RM8yts5gaDdixgLPVU2aHVb5G/xqzMZi10+zyx3LJdNXbykjB1fkVdspwN2co/PTQOzzrc9Ld4RafSFqZshiZcsW74hjU4+2z/gA9rrB6xlDDFksNV808p+znzNqZ1g36ty0WR1zNz7bZXYULF5uwFY+ssicPOPZkd2rkPqV7yLJIceMYJ5Gr79NUACPa7Sn78FqeYcC1nMhsoMBssry2OguLuPEWN7PWo/xdro5ZaCHs8+UvsYbQg9xPX7AjU1ou2quQTSf34TeVk1aVrO3EU7421RbkmHO17C26ChasTZdx7MlZoyMr2SGOWdJZG7HKWlFZxXjj2OJ3mRXGdjwlT2HWeKyLtxoUrDtUKeNnCfH8o7SY2OXqO1gPo88YuYWIkrXq+szKcMx6HjV2vch4Esw6T7ECRnctIDzPmSOzCsPY4qN9wI5VOU+uVzn25HfnyLxqQ50F/b6d9/YHtoMBrKnSsCulz6ZAtINNCzv/KJgV31bMumDmquNxLEMN9CwW+vxWNeRBLQsWM9WU2WR8TtFn5n18GNcH1vlrsm+16VTrZxkxuy+zz22UWXe2wltsDIJHZC2ogue0BbtmO568FMyC7rWs3xP2sLpir7fBjLOdmWUSZY3VgOr1rDbU3fpZAMAkXAMAxNgg8PtYiKkT2Nn+Tn5uJ35SmnHkP8GMX9w9T4inbPVWv74PMAALFr8cbPAEidu1/DQNRCxG5TLsPW3P6bGd+wO7lhK/sW/bt0Lf0tb6TGncYJGzYVHjFya3+d6UhrhsCp4A3WVac5VOjnkwu8Iv6HvPX0fGLTeDgRUlW9+0b1Y5C/WmL3S9lAqNBuOKr8c+lpeYCrseLSbu9Gz/Rcm4WgUv3RT+5isAsBgUZTlETsH1WBT+DWef4Z2crScZSy/ndvveV15GVrK96dDibbhuz+01aYKRWywYO4Ms4Oav2mNzbid9sLWx5aK3k6jxZRtzemm7KfdjrLk5fnUvFXfWmLMs0sTtqLAT5leDnaDccpz84xesgicys5feQMkv1oPSxp7VgcUWO3Gjl9tzhtwXulkEXP9Fi5vBwE6eth60MWXtEYufyXfyC39r8bKa8XF5g2dv2d9nR96zLId+brFxPX4AAHA7t2NRVaQFLzuZnl4LcLtpUcE+/96DPKnmNpycM379oT13EAL2v2zHsvKmPfbSXYuRh2b2Re6VJ2zcArcoRxawX3M1illqrSzLplyc5zwIAJixNXbD/Z/R27ji9jJkqRU3J4H7pY0CoVjhY+36yKfXjrj9BhsReIubC1fsNTZGFntf+ZidB4XK4qXia26MIsoxt5dqsFlKacGiye3zv704R04Tg/ySPn0IkROJ02ifacv7shU7ftV+xufaOLNWeKy0mwCAkgtaF3m5wnPv11c5+cw5nZzlOwb9y3DPtfft95STkRrbZJFjQMMSBsE+91U8goZjSsbJZh6isLXyOACg5CTgFieb18stjBgPW61N+GysfAwA4HvfBwB4rn0VADDL0qSjTSJVbh//pPp5AMBd/2UAQBPP9oKXtnqJiIiIiIiIiHTUuc34OSjRxGJyTN1qWADKsUVum1eITCOLnMku0nwZU55juajaypszZEP7e497vQZcYetxRT3njGSfP2+QUsjqCQbcWpZaGUYtbSwNz8KCgdk8DT/zmiuZDVewKkS4VPSbxXQztsNd5wrEImU+S6mqBQbMAsqZgbbe2n1rlcVnu8+UWK6uDVuufvlbCF7FwJdZzf/nfdommFor837WtcQsBKDlSicLYlaMnU3GDpjtUaYe2y6g1+P2jcZihvlEuFjbKnx2137+cGqX63w/wzhH9CrSu6wmzMxa4Wc/5b6IhoVPM65q1a5FwWy/hj3YW66Yl9zSk1KgF8UyfUDY5uvwbKBkzJVje616bCtg2cyOUXNmGe76Caa3bAVMWYbLqeHn0pbcOsqV84rbIzy3hTYuwDFmUlp7ytRwIx6fVvJ7LgvvMOJjV5kF9OSKBdHjbA1fcmF0wO0XG8w8G7QB/zeLZy6Ok/fjF5b7Iv3f3DJzsHKpcYndHlKB5ThFFmw88Dxn9jwH8pk9Jp0v9/kapXNYZVOTHtvCf4DnSBf5A9rbfC4bEqzytUauwa83bNnMc2nFzbLh96Aes7oG3GrlWfogWJZPiz2kSCu4bSukT7O6DgAouZ25Zra0zyK2Wp4b8xz5KW5R3cw5TjFmch4fB0XKjAW+2LOCvvtz5TwsHw4uHCeKbJOXVvokOoujaQiI3F7aQ8oi4/kM46fP41I6Pg2dwwa7VFxilusWj4Utv7uNBh+y1+DYVnDMmbsZruzad6tf378CQBk/IiIiIiIiIiKypM5xxg9Xt3jpmXEDrl64wPaC2T7gbK9f4P5Tn7J2StwjtWsOLqKOaeaRP4dZQy33DbKEB3wzBgBMg12O/RXUcZvvUWsZyyZwBTW1jmxdKugNXnLFKs4PYokrYEXLz3MltbFlxlhMhcMCCr5Qj48dMdNnOGF7y7RxeWZtC7PaVkamzUvwIdVMUNwslxQTHD9YZyVyNatlHOQcjuswQ6qa4lmZ2bP99ipX1B1fo0hFwKNbZByWvBzxdVe5rX3AQqyDOQvKt4ylZowMqWCmYmfZNIybwMYDDdsn1/ysHFdLmzBH62wlKnjLEoo8ZmHA4rtpvOKKWfDAiBlD8Kz7M7bLVWaODVhg3rGWXa9hTM73AJ9WvhQ3y8U+U8/jVe3ubUNbL64xDtwUkecgi+NWqgq/njJ/bAxybK3tqogBMza2WIPlMZ4TPc7zno1dZhXus6lFa9fDbB+51/FqWS3iJkvnvBYTLceayCK8EXfgYio2z5ocTAYKzsagkse1AT/nLDZY5/Fsg2dOTzHD9TLHupXrzDqc8bjH9xPmYxTNHf5s1aNbRul7S2pG0Gapcnef99t1X4xx8P8+M5mZBehbGxsC7DnzaNkf09ji8cZi8UFnNYQ+wqLR64zNisPYgMe6VR7f2lmDTX5pu6ZssaXlUo0ffq6OmT8tY6FxPp3qgl+z4R3HBx7ZYrqDGUG+rRZNMMBjVpaaZzA+hqxrljITR327nKKHh+ZW4yzudyOzWRk/IiIiIiIiIiIddW4zfg5X+QEOahQcbdPmMFu0/HOcjc64muW4F9Cl6cfFawb4kOomMDsoTzPMnJFsbRm1qu8CAMatddW52b6EalFvQ/PRy+PeektZkdK9UqvSVGsltXdvAbYaxGI/vF2URcrwYIw0WFwvuDK7lrMeEH/KCpfR+uysE7jPfVbfBADsN68jRrWmXE6pXXGKnbQCllYgmAHk0opYg7TylWoppKwwt6gj5u65HTGmrdEYcqVinRkca5zfX2dsDficPsOyaT16LrUOP/xO5XRl917mtioaWeMnpOMQUtxMDtqNcuUcwY5njp/vwSoXeDuwyfpzAw5hF1M9jcbiM9UZy2bMFmKtn51pRB61drSc0vGK2aRphZTHEX8k2zTGKcBWuLFhFldtR5+8YGttxlDO0CqqgII1xrbYbvsyz3O2eB71CE+nBq39pTe349d8uoc8qhfc8klxY3zG82LPjHUelxY5zvHuYoXeB6vBkfKZm2Cfb8ZzosazLh1qbLA75UN88KOeccNMxQcYa70p623UluUx3d9G4RU3Z0Es2Lad5zVYZIvxsmiRcg9DsNqVgfHVVnZe65hZNnd2vlv4BmutjVMXM6tiuMXj00q04+PjzDwbZjyucYybtTOM0vcvZYstLcfaOxk7UmbsDhd4ngzXLjrHpZQfx3OWlvUQA++vU5v3OEXNDnIVa5FNee5Scexpa3YjzO/Nqp+5gHlrx8Q2psz4s01nbSIiIiIiIiIiHXWOM36M5woDWHvHZZwRTvV6/CZcfsmuOHbbKm1G0q1zJpt7Sgt2Q1krHC5OWC9hbqtlj6R6G8z2qAvL+InR9isPBzbr+JHeo/hfX9q5f7+g3CfM1mD1+GpuKxS93gW7m6sLgStkvslQFBsAgLywGev+yOJll7PRJZdh15m9MRg6tKyvEbjSlTrsXGYHphmu2mP7FjdPrdprPlN8HD/30v9yv35Zua9SlwBbvaprWz0oGBchS3U2bCCJ9RBZz1Y7ytyeM1hh7JTskFKyw06P2RhlRMNOFXt3LFb2uHD/WFoRG1jMboxs1eLyyPH2i2h/ye7TGuoysbGk5IrXtLLjQs696j614XL2eWZ1jl5uWRqDzJ6z1rf42WYG4SY7v20wjrb6Aa/tWyzFhqtn7Ca5yQyxyJTEFWYTbW3Yz3968xLqbWWnLid2TSrtGNSwixLY+Say1kWqVZf5C3DBznOK1lbOFx11Jjb2ZOym02PH0ssrETszropuW6zObrE23dTOkS72LGZWWR9o9QK7yxUPoX1DY87yYUckjjFttC5IrngIAODZ5SuyG1zeLtbe0bBGVJazjlR41O7gORNPkbBVZnisZ+fSH+BzH2ONnwe42j+cWVZPn+fNvQ3r6uQeXEF4cfc+/J5yUhxTj6sJMynSzgjWm8t4PHHlw4tM+cgugKkUWTayTk79aMezzdbOhx6Fw8fqxwEAj2Q2tl3ct2PdgJllD/JrWZEik7svwkqJ3f1X+C6V8bNs0kiSsXsXgn2+c9aF6/O7cwjlIqZSBo5jnuFaj7FWc1dF6ooc+xjw+FWzRuEkdQDjc4vWYnCfWUPb/GLf5jPc8dbNK3RkV4UyfkREREREREREOuocZ/y4t7waF7U12B3FbcMFq8MTvFUZ97WtPsSJzQy6yubPGs9sHhdQsytTSHVeOMsdwE4Hud0+5er/jbnV+Nmd3tYK2FmwiJe01/3evcou20DkSny6raltFcuxDkKqt5E6gXkH1Knzkk+PSRXombXBlVrHWJvUtvp1Y3JN9VmWXOog6Lgiuqj3FW0siKkQR9YDOP54b5mI7cyu571ULyrVJrNLHyMadkCJXD1lMhBGrOGS+Xu7GKSmXtOmQbHYhy/Lxsd0DEn1N9gZKd2e9rm7HnzkWMPV93ltK+uDvo0rLWvZMbkHtY9oWX8ltePpc2V+lWPNtLFASfV8HMei1h+stMmySbV7UqaPXaQubyF1PVnU+GkA1kBAZRk/bp8DyK4dt9q+rYg2NVdOy4gwZqc3ru5fSF2+UhYrE6oHHHNSx0E39yihMWd5pcywdKxK568pU8Jub+OY9QyBuOgcl7Lo7by5yGwMqlmvpXYNyspiaJVpQJv5vdnPOY9N/dSpMmWGzDwGbnh/fkU5IYydlFaQpzNTXqaOuGF30ZEy7abImC3kWB8qsJ5dDCnTzCHj8SrP0mXKUuOPmfF2ZrdmPZ7vBKBYnLfrLHlZpe/IKDgI9Di+sLjctB7DcdxYZKUyQ/FutOfWPOClc5YYIirPDB/WClpl1uKIWYZT1k31qY4ZO4X5bIoqjvne1NVLRERERERERESW2DnO+Dky48uZYOe4igpW7463gMiuKd72ksbarjdj1vypWPfF2wzipPYYsA7QqLUV2BlXYH2w2iwZb79R2d7B1+YvAgCuttfe+68mJ2axgurSzG/F27lSwc4CWVbDgXvRI+s5cZ9y5B5Sz5nnirPWE+9R83XSrHPkqkbq4DPqW8xVXAHZndus+JV6e5G1UXPVX5ZFWlXnysWiswS7k6SOXakWQlYDKXa8jRexsVXOLMVb6kTAldN5ExAYR46x2StYI4ar8AVf3wV2heJK2aytsJVbPYbr/jW+t26sbJxtrE2QOnSlMSGtiB05hjnnEDnW+GDx0nCM6fF4VjNuxtFuL4JHw7/71CWMY05qVtln56YeszYKnja0vsYosxpnVVCtn2W0WKFMrSPTmLNY80tFNRwix4nAunJhZuOV334YANAUFlMzntvs5wG+4rjEemKj1MWLNelKnlcVXKFNXcB87bGVWR2PK+FVvhPFzulLY46NBcExqz2mekype2mKmwkiu+Qsxg/GmAtvAABqdlmaRTt/nsQaNbNTPTsVFukydcNtOAYxRSNPWaqtxxa7Ob3qX+R7kmWSOiQvzpEX36nYIc6lDLEdION3K2bBcwiCazj28DtVyw6lVQiYsevgmOczazzGBb7GkGNOzhgtWntcE2ssstFk6aROa4H1dqv4CgBgGh+w+9kFcoYxCtYwDMwiTB24KmbKV2CmGMerWWzQD3YOVPI71ogZP0Nmns7iHp/DTqg8Zs79Du60L/PndeO8WBk/IiIiIiIiIiIddY4zfoxLmT5p3YCz1I57BR3uwHHW2bXsLNDYCobnFsSMe+PbwIyLwmO/tBnJlcZmKcfe9ju7cBsA0MxtJf9K/ToA4KXGLm9yhV/eB19TUZxFShgvmOHj4uGbUxkOOFcjcuY64yp84TftvtZmpR2zdrxP+1RbtNyr6vLUASHV82CXryH3OgeLwf3WYm4c/aKTT+2V8XPi3kvsMNPGpZWFRSyl+gk1IjsKZJGdnLx1t8hbxhTHnMDaB20egNJu65WpWwH3unu7LFL9BK6QpdG/iSUe7n8YAPBc/WsAAN+RlY2z7d51mYyfn0v1nRY1NVgPzLUHq+2LbENbEYvMOG1YM2HCVdAieLSpZkYavArWisotBoasETVirLGpE+Z+gIv50wCAnaBMseWS3XPpFgk+acxJmatpNb5e1GpJXd1YDgjhjmXk+MzOf+rMsjPmRYRzPKalc6Q0qHDpPusxizEdIJnBEQA8kH+AP++L9taO+6vKfXT0WJVqyqVV8DQG8bwkbw8dt7J7nuMbWyX3rN9SMeNn5hrssdvthJ1P57ld1qwr1uOYlhKsPWOyndfYyi0DAI2qGi6ndH7DsSWkLJu0i6Lgxf6i0xdSDPGjDDwnDkfOkdvosePt2JbzOJiyxIbsmnoxTx122XluavfvhX3UzAhRzCyvmOr0NHZOMYEdbypnu2FiVqDHjm6A7aJwqU5P6vLFc5q+YzYYaqRvRQWzgKa87DE7aI5bfASzzZhhNAk3sc2uXl2Jm3M/8ZPSEltuvUrbLnqFHayQZUDLVm4spNtWFoDl4Al7Ss0UMp4QrQxWcPmWnRBljU3kvDT7CgDgxuxL9rqF/dNfrZ4HAGy31wFYOqJSnt8nX9M/czqYWXw0Pm3FsgNWzgNXxqLd1Xz7ID26ti/vYNzkM7tepO0WucXaqMzxVGmE6jJ6AAANz0lEQVRpzJu5xdQDA7u8tGaD1O6eDU47c4uX27XF5tRNMeHkorwPvqbYSYW67USkifYFKufBK3ByLxX7bpo5EG2CONSMocrGkfGeXRY8sI0KO/CFMsenL34IAHCJRXofZmHOtT7T5+epCCJ/HlOjRysOO/Xv8L3qi/vysM+nYIv2Km0FdOnEll/U04lK28CxyHzL0xzPSec7t28CAErYWLPGL/HTvIfv3Ph6AMBltod/hJeb3J6zwonKPicUy4ITT6MMgytjvgejI9eySP+vc5HKDXj7gPemBS5u76odIlPhIyxWMOP29FtXAQA1txJ7Z1/gfdbDv1Z+GgDwCCcY08+7za07T13kCTp3CLUcm9DL0cSb97xXWQacsGO8tD4euTctdLG1crYBl6r4pi3EnATMYYsUuec4xS90be3wodrGqcvcvjrdtet3uWXj4YuMMTY8iBxh2myIWdi+D7+nnLRmz7b6hXmaBLbPuDe0Cd8421tM6DmwYQ4nb9a4/WY9FYtnDG2EARouetZciNhfFOO1WNntWRzuTnk7z3PG2T622/TlXpZVKonQ8LtzaO07c8bjT5ZdQO0sXgbFgwCAvGeX631rwLTKCcMRG5pcxBZGsGNR5DbkjD8nbQ2cZ1t8ByzFsVjE2MUspAnDbtBWLxERERERERGRjjr3GT8HuPLFFdO6suyJrIwAVx08Z5hDY63Xi9ZWwnzN1rnBVtEmWYEdFrTz3maYK28ZGovVCq6mzhYp+Kngq1a/llta8eK2GfaQzPl55oVdz/IpEO5t1x0Wn21qpWuPnTZsn+sd4txWPHaZkrqfswh4ZquxBVc1bs9fAQBcrezylr+Ng3V3WS73ps8vYoZbaNKqe8a0VO8ni9bujoWgF6+UWnhz5T54W/loY47JxF5nyFWyGdPmK24HHOXcqspMEs+2qFU1xaW+pc/nLBbtU5q2nKIUJ/b55WWKiSQeehQQQg3wGJS2ZoS0VWNRGJpZG9wWWrkS+60dq1aYRVYxK8izcGKvZxlHA45tZXnQHvfjw08AAF5sfgsAMIe2mS4HZvkVNgZkeWo+wNSb1NfYpSKYNaK/N55yrpRHps9njK0spssS+0yB3wsWT+PMMp1HpcXM/p6NJ0O2Vu63LAyOBo/2bOU/q3letWgVLqdusYWdBZvZkju11XapKK+bw3m2zWbh+BQf3CmKgreXrR3Lihgx9nYenErCr8ZUON5s79vxZ1CWfC6Lt6LCamExhlrnO8uJ57feMr5Czcw+ZsnXjWWhBtwFWGDXM+PH8RylLex8xHN8apmhWKHGNZbDmDPLsOZWwnUer641lrHBwxUcx63buKXj0xkSU/by4pyXx7Cwu9hSXLHo8rSxzPdRsGPKJFh2zy6/s++FAVai3ZZzrMkZp302byp5Tj2F7ci44y1j7UZ46dAWwW5Qxo+IiIiIiIiISEcp42eBreSYpVHXLMbcjoFUTDPVf04zj1wdT+0sU70gB4edVIeBs5YBqZUzV1I890irpsaZklortw3r6XA2Ouee+FDYioUPTQqpRaZYy73vGYvRgSthEz5uGwHXgq1IOK6y5vx5BV8sFTEbB5uVnvLxLbxiaWnZ//MtV8CamdV6Crll+6XupxlXUR3qg7IXrAMVWBQerIEQYxo/7DlzAG942wu9y5X7mjG5zf3Q45Cea0XrWsbYXb+DZ5tn7ba0X16WAD/HxrJG89ZWTjNm5oSU3cMxISvdQYmmRXxYjCG7N27aRUHDHG/MLXN1whXUNrcW7dPc6o1dH1s2x4BZJH1mHU78FFdaK8CoDLFlw9ipbdwoWSPMOdbx4cflWJew6DVIWUIuncfw3KVkfOU87+kt2uLmuO1/FwDQBmatOouZtrGaC5PaYncls9cYMQNp6qe44jkOKtNniVjc+NbOLwKPVVnBVtysr5IVDKD+LTiXCnvbZwye76SaP5G17dLY46PHdRb8rSOzNzIbcy4Gi58bDIkh42bAmpjbYQe3YqrTorhZTvy+5FMxZxuDfGtZXr6yTApk7aHjFDN/0ng0smYTGTPDcjbOaUIOz4Jhe2xUsMcM1RFS7R8e8/i9zDvL1ng1vICK5z5yloR7LmNsFzW/Uuv3Ntj3sTrYOdKYY1HGDNcCBYaw8xh3ZFNNxnjacg8DAPb4GjvRdunM4/7i+3tXKONHRERERERERKSjlPHzJsz8YaZF2pf6lt6UYHEwlejjO/c5UdvbsyqtiKVsDVtBaJjhlbLAsixHTL1IY5qpZtZOmjwOR+5HXKy2xsUsdzz03wNplVQ1oc6OyDGlmlmGRVopTamEjisPZdFHZJ2eGNJ4xLoJRcokdIefijoGNJXdxuZLuMbH9DnM3+VKfZveB+sHVbFBjZSZqHFpeTBTjGNNPbWV0hQ3KUZSBmp/uL54pmfnipjqsuQp1iwmqrTSGiNeZozdZPbYHbZI3XK2Cn+bmWoZx6m05343TvA7kRkfyhRbMvcep+p9q8XjmAUYF8kSNp4M3CqwyERlvUOe+5SFxUHBLOWC9ceyANxqLSNkytX3hp1Txq2t8u/MrYpLjyu06bznZtjG73jrJKiMn+WT6hK2KW4KGwMcsyoCuwLGMF7UaYFPXXBSly/Wa2Gmc834mgeP69Hicj9aPI6jjV1b4TIAYJfxk76geB6frobreC1YXQ+d+yy7lCWW/v9O34mYdRMObksZHJHZYlXF7DFmhAWf2nVncM5iZcIsoX3GX481WvaCZWq07Cq3F60m6/X4MryOUx1x9P99izXvJ7zGnROMqwrAnKOJW8Tcva+xz9pRqZ5Pw+5esYPHJ2X8iIiIiIiIiIh0lIvx/Zs1d+7o7jrpihjjibVYOFtxczjTyx257aijv9YZ+jXvk5OMG2DZY+fe+Eid4mI8dI9LnZzs8ugvk1Yv3KG/H0idCtnh6U1ZZEe6zJ0x52fMuXd9xqXsQnaBc+woGGO7iIGMj0md4jLH+lE83ufM9ChcjiE7UKbfON2Xc5/8Xa6gplX31IGyifWhve9L9M/1VZyvMeftYod1WRgfIc4XY0yeavrkFjMFa0ql2nQ9xlIPBR7OrItKy8zX9JsPUl2xaPUSaq6eTrmauhu3MWGdurO0onp+xpyjeBxivMCl+pbVwTGK2WQ567TkjJOSXXNWYJkaIwzxRP4NAICG2YSp0N3AWR2OGW7x8iBeAOBOvI7dYFlmipsDyx07x8GsQmZp9DierGALj2YWOylmSmb+rGdbAIBJtK5hFbszXQ0vAgC24xW0R7qkngXnd8yR9+Kd4kYZPyIiIiIiIiIiHaWMH7kvNCstx6GVsK/m6D/PW/9zHc74Obp3+axn9ryd8zvmuCPXUjZYPHTPvVlk7kg5v4NMMYcea/scrSeWXrdilkaq/xQXl0v8T/QOzveY8/axc3Bbip206l7e89xssRqfYZ1dvDzrhqXXSc+pYDV+Ur2E5lCX07OUsZGc3zHnqLfKbE733Jsd5FhPLOcYlLsSl9wHAQAtuyylroCOcdOwG2HFjJ8qTvm4+kzWxzzfY857cXCcssscK6w9hyPfXVOGWRqDanZ8qljr56x2ZtKYI8ehjB8RERERERERkXNIGT9yX2hWWo5DK2FyXBpzvhZv90/lULCmTzxS++kgfyh1EDx7GRpvRWPO1+rtsgwdSnbSCW/KAkvPube+2FmPIY05x/Hmf7I+rGZLysJ4u85uASmTTHHzTrobO2/m3pSvcO+Yk+4/6FB6tv9pNObIcbxT3Kidu4iISKe93fldRKsi8/KO3joeIiIazBd/fzfPkfPozbFQcwvX28eNO3JdxLz9JGD8KveLCKCtXiIiIiIiIiIinaWMHxERkXNLq+pyPFpdl+P46nGjMUlE5CQo40dEREREREREpKM08SMiIiIiIiIi0lGa+BERERERERER6ShN/IiIiIiIiIiIdJQmfkREREREREREOkoTPyIiIiIiIiIiHaWJHxERERERERGRjtLEj4iIiIiIiIhIR2niR0RERERERESkozTxIyIiIiIiIiLSUZr4ERERERERERHpKE38iIiIiIiIiIh0lCZ+REREREREREQ6ShM/IiIiIiIiIiIdpYkfEREREREREZGO0sSPiIiIiIiIiEhHaeJHRERERERERKSjNPEjIiIiIiIiItJRmvgREREREREREekoTfyIiIiIiIiIiHSUJn5ERERERERERDpKEz8iIiIiIiIiIh2liR8RERERERERkY7SxI+IiIiIiIiISEdp4kdEREREREREpKM08SMiIiIiIiIi0lGa+BERERERERER6ShN/IiIiIiIiIiIdJQmfkREREREREREOsrFGE/7PYiIiIiIiIiIyAlQxo+IiIiIiIiISEdp4kdEREREREREpKM08SMiIiIiIiIi0lGa+BERERERERER6ShN/IiIiIiIiIiIdJQmfkREREREREREOkoTPyIiIiIiIiIiHaWJHxERERERERGRjtLEj4iIiIiIiIhIR2niR0RERERERESkozTxIyIiIiIiIiLSUZr4ERERERERERHpKE38iIiIiIiIiIh0lCZ+REREREREREQ6ShM/IiIiIiIiIiIdpYkfEREREREREZGO0sSPiIiIiIiIiEhHaeJHRERERERERKSjNPEjIiIiIiIiItJRmvgREREREREREekoTfyIiIiIiIiIiHSUJn5ERERERERERDpKEz8iIiIiIiIiIh31/wNPeIuOkHT+xAAAAABJRU5ErkJggg==\n",
368 | "text/plain": [
369 | ""
370 | ]
371 | },
372 | "metadata": {
373 | "needs_background": "light"
374 | },
375 | "output_type": "display_data"
376 | }
377 | ],
378 | "source": [
379 | "# Change viewpoint yaw\n",
380 | "batch_size, n_views, c, h, w = context_x.shape\n",
381 | "pi = 3.1415629\n",
382 | "\n",
383 | "x_ = x_c[scene_id].view(-1, c, h, w)\n",
384 | "v_ = v_c[scene_id].view(-1, 7)\n",
385 | "\n",
386 | "phi = model.representation(x_, v_)\n",
387 | "\n",
388 | "r = torch.sum(phi, dim=0)\n",
389 | "\n",
390 | "f, axarr = plt.subplots(2, num_samples, figsize=(20, 7))\n",
391 | "for i, ax in enumerate(axarr[0].flat):\n",
392 | " v = torch.zeros(7).copy_(v_q[scene_id])\n",
393 | " \n",
394 | " yaw = (i+1) * (pi/8) - pi/2\n",
395 | " v[3], v[4] = np.cos(yaw), np.sin(yaw)\n",
396 | "\n",
397 | " x_mu = model.generator.sample((h, w), v.unsqueeze(0), r)\n",
398 | " ax.imshow(x_mu.squeeze(0).data.permute(1, 2, 0))\n",
399 | " ax.set_title(r\"Yaw:\" + str(i+1) + r\"$\\frac{\\pi}{8} - \\frac{\\pi}{2}$\")\n",
400 | " ax.axis(\"off\")\n",
401 | " \n",
402 | "for i, ax in enumerate(axarr[1].flat):\n",
403 | " v = torch.zeros(7).copy_(v_q[scene_id])\n",
404 | " \n",
405 | " pitch = (i+1) * (pi/8) - pi/2\n",
406 | " v[5], v[6] = np.cos(pitch), np.sin(pitch)\n",
407 | "\n",
408 | " x_mu = model.generator.sample((h, w), v.unsqueeze(0), r)\n",
409 | " ax.imshow(x_mu.squeeze(0).data.permute(1, 2, 0))\n",
410 | " ax.set_title(r\"Pitch:\" + str(i+1) + r\"$\\frac{\\pi}{8} - \\frac{\\pi}{2}$\")\n",
411 | " ax.axis(\"off\")"
412 | ]
413 | },
414 | {
415 | "cell_type": "code",
416 | "execution_count": null,
417 | "metadata": {},
418 | "outputs": [],
419 | "source": []
420 | }
421 | ],
422 | "metadata": {
423 | "kernelspec": {
424 | "display_name": "Python 3",
425 | "language": "python",
426 | "name": "python3"
427 | },
428 | "language_info": {
429 | "codemirror_mode": {
430 | "name": "ipython",
431 | "version": 3
432 | },
433 | "file_extension": ".py",
434 | "mimetype": "text/x-python",
435 | "name": "python",
436 | "nbconvert_exporter": "python",
437 | "pygments_lexer": "ipython3",
438 | "version": "3.5.6"
439 | }
440 | },
441 | "nbformat": 4,
442 | "nbformat_minor": 2
443 | }
444 |
--------------------------------------------------------------------------------