├── lesson3
├── eye.png
├── glass.png
├── smile.png
├── README.md
└── projeckt_main.py
├── lesson7
├── 0.jpg
├── 1.jpg
├── 2.jpg
├── 3.jpg
├── anime-wolf.jpg
├── README.md
├── 11.ipynb
└── 4.ipynb
├── lesson10
├── back.jpg
├── jocker.jpg
├── README.md
└── skikn.py
├── lesson4
├── Readme.md
├── TFLiteFaceDetector.py
└── TFLiteFaceAlignment.py
├── lesson2
├── tamrin1.py
├── tamrin6.py
├── tamrin5.py
├── tamrin4.py
├── tamrin7.py
├── tamrin3.py
├── tamrin2.py
└── README.md
├── lesson1
├── tanrin7.py
├── tamrin2.py
├── tamrin3.py
├── tamrin4.py
├── tamrin6.py
├── tamrin1.py
├── tamrin 5.py
└── README.md
├── lesson8
├── README.md
├── filter.py
├── sudoku.py
└── sudoku_live.py
├── lesson5
├── tamrin2.py
├── tamrin1.py
├── tamrin3.py
├── tamrin4.py
├── README.md
└── tamrin5.py
├── lesson6
├── README.md
├── 25.py
├── tamrin 1.py
├── crop_image.ipynb
└── gift_sonw.ipynb
└── lesson9
├── README.md
├── color_scan.py
├── main_color_picker.py
├── form.ui
├── logo_microsoft.ipynb
└── rubic.ipynb
/lesson3/eye.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/yasinnorozzadeh/image-processing/HEAD/lesson3/eye.png
--------------------------------------------------------------------------------
/lesson7/0.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/yasinnorozzadeh/image-processing/HEAD/lesson7/0.jpg
--------------------------------------------------------------------------------
/lesson7/1.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/yasinnorozzadeh/image-processing/HEAD/lesson7/1.jpg
--------------------------------------------------------------------------------
/lesson7/2.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/yasinnorozzadeh/image-processing/HEAD/lesson7/2.jpg
--------------------------------------------------------------------------------
/lesson7/3.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/yasinnorozzadeh/image-processing/HEAD/lesson7/3.jpg
--------------------------------------------------------------------------------
/lesson10/back.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/yasinnorozzadeh/image-processing/HEAD/lesson10/back.jpg
--------------------------------------------------------------------------------
/lesson3/glass.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/yasinnorozzadeh/image-processing/HEAD/lesson3/glass.png
--------------------------------------------------------------------------------
/lesson3/smile.png:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/yasinnorozzadeh/image-processing/HEAD/lesson3/smile.png
--------------------------------------------------------------------------------
/lesson10/jocker.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/yasinnorozzadeh/image-processing/HEAD/lesson10/jocker.jpg
--------------------------------------------------------------------------------
/lesson7/anime-wolf.jpg:
--------------------------------------------------------------------------------
https://raw.githubusercontent.com/yasinnorozzadeh/image-processing/HEAD/lesson7/anime-wolf.jpg
--------------------------------------------------------------------------------
/lesson4/Readme.md:
--------------------------------------------------------------------------------
1 |
2 |
3 |
4 | https://user-images.githubusercontent.com/88095232/143685941-ab22c4a1-36a3-47c2-8398-b4e51c380545.mp4
5 |
6 |
--------------------------------------------------------------------------------
/lesson3/README.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | https://user-images.githubusercontent.com/88095232/142186592-2a702629-485d-4a90-8120-52903ec1ddd9.mp4
4 |
5 | # lesson23
6 |
--------------------------------------------------------------------------------
/lesson2/tamrin1.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | img1 = cv2.imread("Assignment22/hw2/a.tif", 0)
3 | img2 = cv2.imread("Assignment22/hw2/b.tif", 0)
4 | result = img2 - img1
5 | cv2.imshow("Out_Put", result)
6 | cv2.waitKey()
7 |
--------------------------------------------------------------------------------
/lesson2/tamrin6.py:
--------------------------------------------------------------------------------
1 | import cv2
2 |
3 | image = cv2.imread('Mona_Lisa.jpg', 0)
4 | inverted = 255-image
5 | blered = cv2.GaussianBlur(inverted, (21, 21), 0)
6 | inverted_blured = 255-blered
7 | sketch = image/inverted_blured
8 | sketch = sketch*255
9 | cv2.imwrite('Out_Put.jpg', sketch)
--------------------------------------------------------------------------------
/lesson1/tanrin7.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | import numpy as np
3 | img = np.arange(0, 1 , 1, np.uint8)
4 | img = np.resize(img , (250 , 250))
5 | h, w = img.shape
6 | for i in range (h):
7 | for j in range(w):
8 | img[i,j]= i - 255
9 | cv2.imshow("🐱👤" , img)
10 | cv2.waitKey()
--------------------------------------------------------------------------------
/lesson2/tamrin5.py:
--------------------------------------------------------------------------------
1 | import cv2
2 |
3 | img1 = cv2.imread("r.jpg", 0)
4 | img2 = cv2.imread("s.jpg", 0)
5 | img_1 = cv2.resize(img1, (600, 600))
6 | img_2 = cv2.resize(img2, (600, 600))
7 | # result = img_1//2 + img_2//6
8 | result = img_1//4 + img_2//2
9 | cv2.imshow("Out_Put", result)
10 | cv2.waitKey()
--------------------------------------------------------------------------------
/lesson1/tamrin2.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | img = cv2.imread("1.jpg", 0)
3 |
4 | treshold = 180
5 | height, width = img.shape
6 | for i in range(height):
7 | for j in range(width):
8 | img[i, j] = 255 - img[i, j]
9 |
10 |
11 | img =cv2.resize(img,(600, 600))
12 | cv2.imshow("output", img)
13 | cv2.waitKey()
--------------------------------------------------------------------------------
/lesson1/tamrin3.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | import numpy as np
3 | import cv2
4 | import array
5 | img = cv2.imread('3.jpg')
6 | imge = cv2.resize(img, (700, 600))
7 | h, w = imge.shape[:2]
8 | center = w/2, h/2
9 | img2 = cv2.getRotationMatrix2D(center, 180, 1)
10 | imgr = cv2.warpAffine(imge, img2, (w, h))
11 | cv2.imshow('result', imgr)
12 | cv2.waitKey()
13 |
--------------------------------------------------------------------------------
/lesson2/tamrin4.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | import numpy as np
3 | images = []
4 | for i in range(0, 14):
5 | img = cv2.imread(f"image_o/h{i}.jpg", 0)
6 | images.append(img)
7 | rows, cols = img.shape
8 | result = np.zeros((rows, cols), dtype="uint8")
9 | for image in images:
10 | result += image // 14
11 | cv2.imshow("Out_Put", result)
12 | cv2.waitKey()
--------------------------------------------------------------------------------
/lesson10/README.md:
--------------------------------------------------------------------------------
1 | # skin
2 | https://user-images.githubusercontent.com/88095232/148645200-1f09047f-61d0-4e54-a4cd-a6830a8a39a0.mp4
3 |
4 | https://user-images.githubusercontent.com/88095232/148645193-6b047860-b5d5-40d6-aae8-ecd4f06f7a36.mp4
5 |
6 | # blue screen technique
7 | 
8 |
--------------------------------------------------------------------------------
/lesson2/tamrin7.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | import random
3 | import numpy as np
4 | img=cv2.imread("Assignment22/hw2/chess pieces.jpg" , 0)
5 | img1=cv2.imread("Assignment22/hw2/chess pieces.jpg" , 0)
6 | h ,w =img.shape
7 | for i in range(h):
8 | for j in range(w):
9 | r = random.random()
10 | if r < 0.06:
11 | img[i][j] = random.randint(100,255)
12 | cv2.imshow("Out_Put" , img)
13 | cv2.waitKey()
14 |
--------------------------------------------------------------------------------
/lesson7/README.md:
--------------------------------------------------------------------------------
1 | 
2 | 
3 | 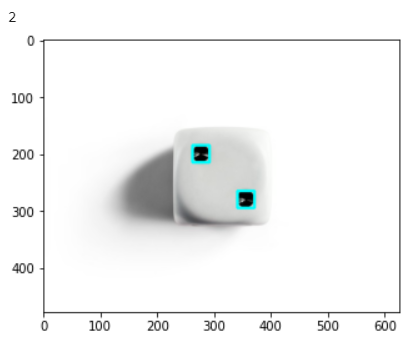
4 | 
5 |
--------------------------------------------------------------------------------
/lesson1/tamrin4.py:
--------------------------------------------------------------------------------
1 | import cv2
2 |
3 | img = cv2.imread("4.jpg", 0)
4 | cv2.imwrite("result.jpg", img)
5 | print(img.shape)
6 | img =cv2.resize(img,(600, 600))
7 | treshold = 180
8 | height, width = img.shape
9 |
10 | for i in range(height):
11 | for j in range(width):
12 | if img[i, j] > treshold:
13 | img[i, j] = 255
14 | else:
15 | img[i, j] = 0
16 |
17 | print(img)
18 | cv2.imshow("output", img)
19 | cv2.waitKey()
20 |
--------------------------------------------------------------------------------
/lesson10/skikn.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | import numpy as np
3 |
4 | lower = np.array([0, 55, 75])
5 | upper = np.array([10, 90, 200])
6 | video = cv2.VideoCapture(0)
7 | while True:
8 | _,frame = video.read()
9 | frame_hsv = cv2.cvtColor(frame,cv2.COLOR_BGR2HSV)
10 | skin = cv2.inRange(frame_hsv, lower, upper)
11 |
12 | skin = cv2.bitwise_and(frame, frame,mask=skin)
13 | cv2.imshow("output",skin)
14 | if cv2.waitKey(1)==ord("q"):
15 | break
16 | video.release()
17 |
--------------------------------------------------------------------------------
/lesson8/README.md:
--------------------------------------------------------------------------------
1 |
2 | Result sudoku_live
3 | 
4 |
5 | usage: sudoku.py [--h] [--input] [--output] [--filter_siz]
6 | Result sudoku
7 | 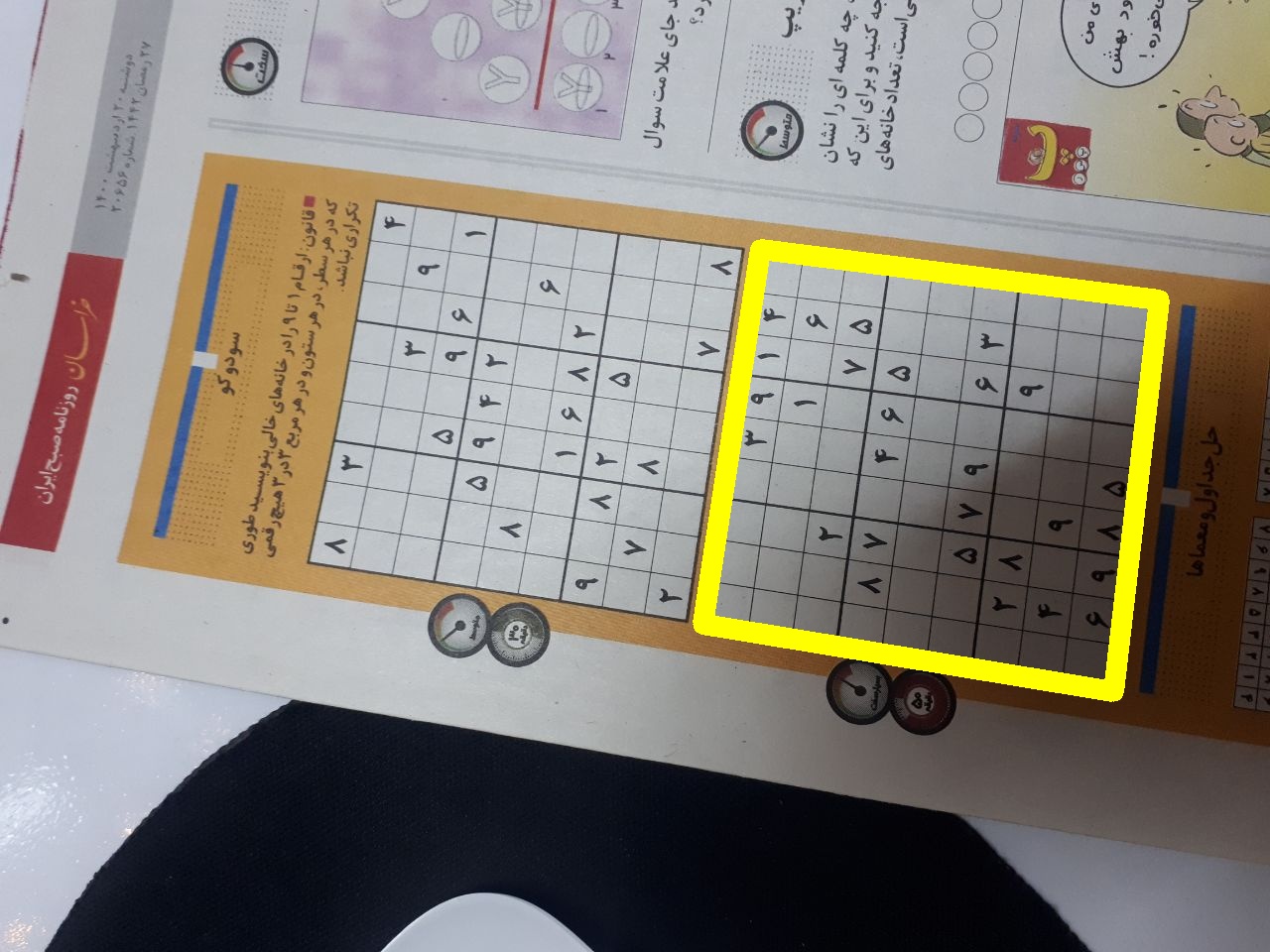
8 |
9 | Result filter
10 | 
11 |
--------------------------------------------------------------------------------
/lesson1/tamrin6.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import cv2
3 | width=hight=600
4 | firstchn = np.zeros((width, hight), np.uint8)
5 | firstchn [:,:] = 0
6 | firstchn[150:400] = 255
7 | firstchn[180:200, 120:160] = 0
8 | firstchn[200:220, 140:180] = 0
9 | firstchn[220:240, 160:200]= 0
10 |
11 | firstchn[240:260, 180:260]= 0
12 |
13 | firstchn[220:240, 240:280]= 0
14 | firstchn[200:220, 260:300]= 0
15 | firstchn[180:200, 280:320]= 0
16 |
17 | firstchn[260:340, 200:240]= 0
18 |
19 |
20 | cv2.imshow('Y', firstchn)
21 | cv2.waitKey()
--------------------------------------------------------------------------------
/lesson5/tamrin2.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | import numpy as np
3 |
4 |
5 | image = cv2.imread("lion.png")
6 | image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
7 | result = np.zeros(image.shape)
8 |
9 | mask = np.array([[0, -1, 0],
10 | [-1, 4, -1],
11 | [0, -1, 0]])
12 |
13 |
14 | rows, cols = image.shape
15 |
16 | for i in range(1, rows-1):
17 | for j in range(1, cols-1):
18 | small_image = image[i-1:i+2 , j-1:j+2]
19 | result[i, j] = np.sum(small_image * mask)
20 |
21 | cv2.imwrite("lion_result.jpg", result)
--------------------------------------------------------------------------------
/lesson5/tamrin1.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | import numpy as np
3 |
4 | img = cv2.imread('flower_input.jpg')
5 | img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
6 |
7 | result = np.zeros(img.shape)
8 | mask = np.ones((21, 21))/441
9 |
10 | rows, cols = img.shape
11 | for i in range(10, rows - 10):
12 | for j in range(10, cols - 10):
13 | if img[i, j]<200:
14 | small_img = img[i-10:i+11, j-10:j+11]
15 | result[i, j] = np.sum(small_img * mask)
16 | else:
17 | result[i, j] = img[i, j]
18 |
19 | cv2.imwrite('result.jpg', result)
20 |
--------------------------------------------------------------------------------
/lesson1/tamrin1.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | import numpy as np
3 | width=height=1600
4 | board = np.zeros((width,height), dtype=np.uint16)
5 | color=255
6 | for i in range(0,1600,100):
7 | count=0
8 | for j in range(0,height,100):
9 | if color == 255:
10 | if count % 2 == 0:
11 | board[i:i+100,j:j+100] = 255
12 | else:
13 | if count % 2 != 0:
14 | board[i:i + 100, j:j + 100] = 255
15 | count+=1
16 | if color == 255:
17 | color = 0
18 | else:
19 | color = 255
20 | # print(board)
21 | cv2.imwrite('chess-Bord.jpg',board)
22 | cv2.waitKey()
23 |
--------------------------------------------------------------------------------
/lesson5/tamrin3.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | import numpy as np
3 |
4 | image = cv2.imread("building.tif")
5 | image = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
6 | result = np.zeros(image.shape)
7 |
8 | # mask = np.array([[-1, -1, -1],
9 | # [0, 0, 0],
10 | # [1, 1, 1]])
11 | mask = np.array([[-1, 0, 1],
12 | [-1, 0, 1],
13 | [-1, 0, 1]])
14 |
15 | rows, cols = image.shape
16 |
17 | for i in range(1, rows-1):
18 | for j in range(1, cols-1):
19 | small_image = image[i-1:i+2 , j-1:j+2]
20 | result[i, j] = np.sum(small_image * mask)
21 |
22 | cv2.imwrite("result.jpg", result)
--------------------------------------------------------------------------------
/lesson2/tamrin3.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | img1 = cv2.imread("Assignment22/hw2/board - test.bmp", 0)
3 | img2 = cv2.imread("Assignment22/hw2/board - origin.bmp", 0)
4 | img_1 = cv2.resize(img1, (800, 800))
5 | img_2 = cv2.resize(img2, (800, 800))
6 | img__2 = cv2.flip(img_2, 1)
7 | sub_imgs = cv2.subtract(img__2, img_1)
8 | result1 = sub_imgs
9 | cv2.imshow("output1", result1)
10 | result = sub_imgs * 255
11 | h,w= result.shape
12 | for i in range(h):
13 | for j in range(w):
14 | if result[i][j] < 0:
15 | result[i][j] = 0
16 | elif result[i][j] > 255:
17 | result[i][j] = 255
18 | cv2.imshow("Out_Put", result)
19 | cv2.waitKey()
20 |
--------------------------------------------------------------------------------
/lesson1/tamrin 5.py:
--------------------------------------------------------------------------------
1 | import cv2
2 |
3 | img = cv2.imread("poster.jpg", 0)
4 |
5 | cv2.imwrite("result.jpg", img)
6 | print(img.shape)
7 | treshold = 180
8 | height, width = img.shape
9 |
10 | for i in range(250):
11 | if i <= 100:
12 | for j in range(100-i, 250-i):
13 | if j >= 0:
14 | img[i, j] = 0
15 | else:
16 | for j in range(0, 250-i):
17 | if j >= 0:
18 | img[i, j] = 0
19 |
20 | img[0:600, 0:40] = 0
21 | img[560:600, 0:541] = 0
22 | img[0:600, 501:541] = 0
23 | img[0:40, 0:541] = 0
24 |
25 |
26 |
27 | print(img)
28 |
29 | cv2.imshow("output", img)
30 | cv2.waitKey()
31 |
32 |
--------------------------------------------------------------------------------
/lesson6/README.md:
--------------------------------------------------------------------------------
1 | 
2 | 
3 | 
4 | 
5 | 
6 | 
7 |
--------------------------------------------------------------------------------
/lesson8/filter.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | # import numpy as np
3 |
4 | cap = cv2.VideoCapture(0)
5 | pixels_list = []
6 | row=1
7 | while True:
8 | ret,frame = cap.read()
9 | width , height, _ = frame.shape
10 | # width , height = frame.shape
11 | if not ret:
12 | break
13 | if cv2.waitKey(1) == ord("q"):
14 | break
15 | cv2.line(frame,(0,row),(height,row),(50,100,150))
16 | pixels_list.append(frame[row-1])
17 | frame[:row] = pixels_list
18 | row += 1
19 | if row>width:
20 | cv2.imwrite("filter.jpg",frame)
21 | row=1
22 | pixels_list.clear()
23 | cv2.imshow("Filter",frame)
24 |
25 | cap.release()
26 | cv2.destroyAllWindows()
27 |
--------------------------------------------------------------------------------
/lesson2/tamrin2.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | import numpy as np
3 | images = [[0 for i in range(5)] for j in range(4)]
4 | for i in range(4):
5 | for j in range(5):
6 | images[i][j] = cv2.imread(f"{i+1}/{j+1}.jpg" , 0)
7 | images[i][j] = cv2.resize(images[i][j], (400, 400))
8 | image_without_noise = [0 for i in range(4)]
9 | for i in range(4):
10 | for j in range(5):
11 | image_without_noise[i] += (images[i][j] // 5)
12 | img = np.zeros((800, 800), dtype= np.uint8)
13 | img[0:400, 0:400] = image_without_noise[0]
14 | img[0:400, 400:800] = image_without_noise[1]
15 | img[400:800, 0:400] = image_without_noise[2]
16 | img[400:800, 400:800] = image_without_noise[3]
17 | cv2.imshow("Out_Put", img)
18 | cv2.waitKey()
19 |
--------------------------------------------------------------------------------
/lesson5/tamrin4.py:
--------------------------------------------------------------------------------
1 | from typing import *
2 | import cv2
3 | import numpy as np
4 |
5 | image = cv2.imread("logo.jpg", 0)
6 | def convolution(image , dimension):
7 | image = cv2.imread("logo.jpg", 0)
8 | mask = np.ones((dimension , dimension)) / (dimension **2)
9 | result = np.zeros(image.shape)
10 | rows , cols = image.shape
11 |
12 | for i in range(dimension //2 ,rows-(dimension //2)):
13 | for j in range(dimension//2 ,cols-(dimension // 2 )):
14 | small_img = image[i-(dimension//2):i+1+(dimension//2) ,j-(dimension//2):j+1+(dimension//2)]
15 | result[i ,j] = np.sum(small_img * mask)
16 |
17 | cv2.imwrite("result.jpg" , result)
18 |
19 |
20 | print('''enter the dimension image\n3. 3*3\n5. 5*5\n7. 7*7\n15. 15*15''')
21 | option = int(input())
22 | convolution(image, option)
--------------------------------------------------------------------------------
/lesson1/README.md:
--------------------------------------------------------------------------------
1 | # assignment_7
2 | 
3 |
4 | # assignment_6
5 | 
6 |
7 | # assignment_5
8 | 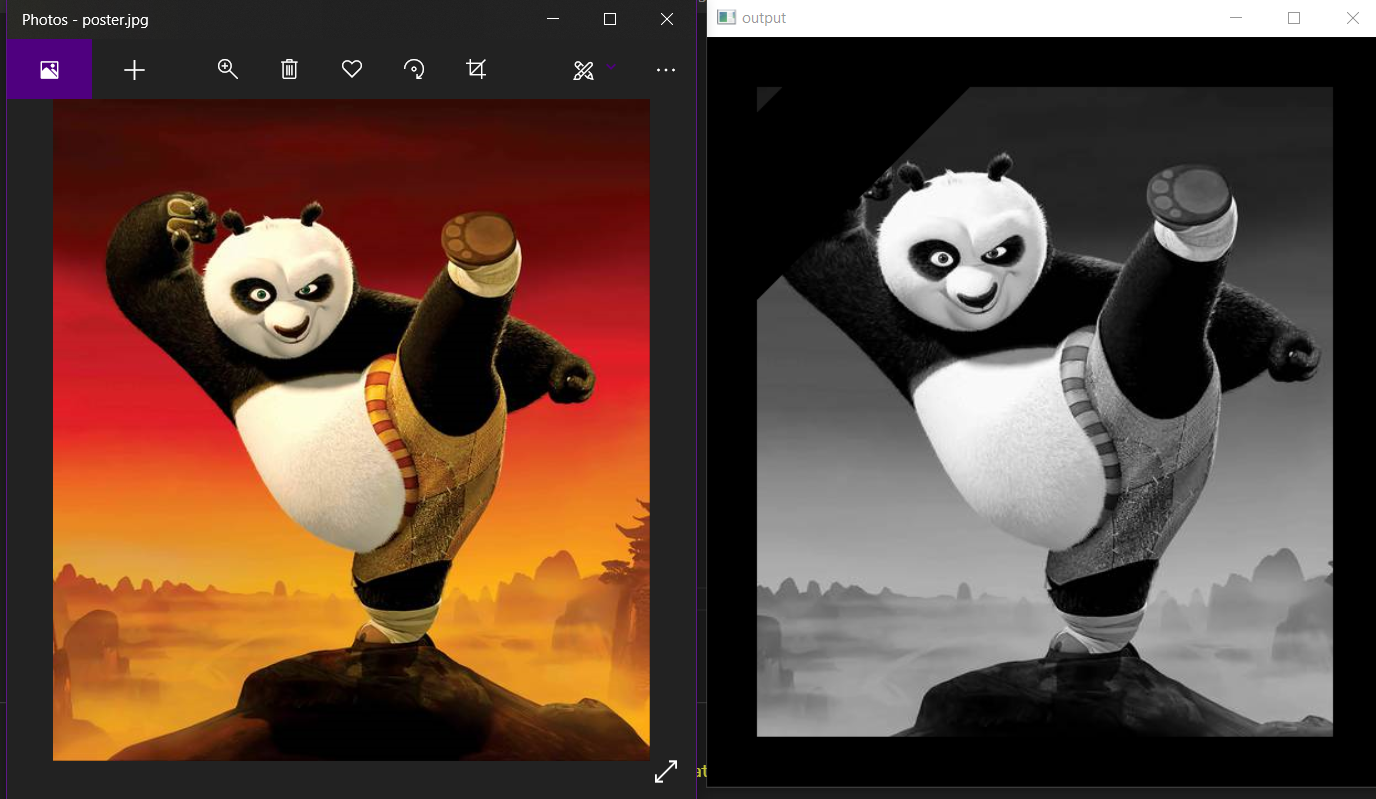
9 |
10 | # assignment_4
11 | 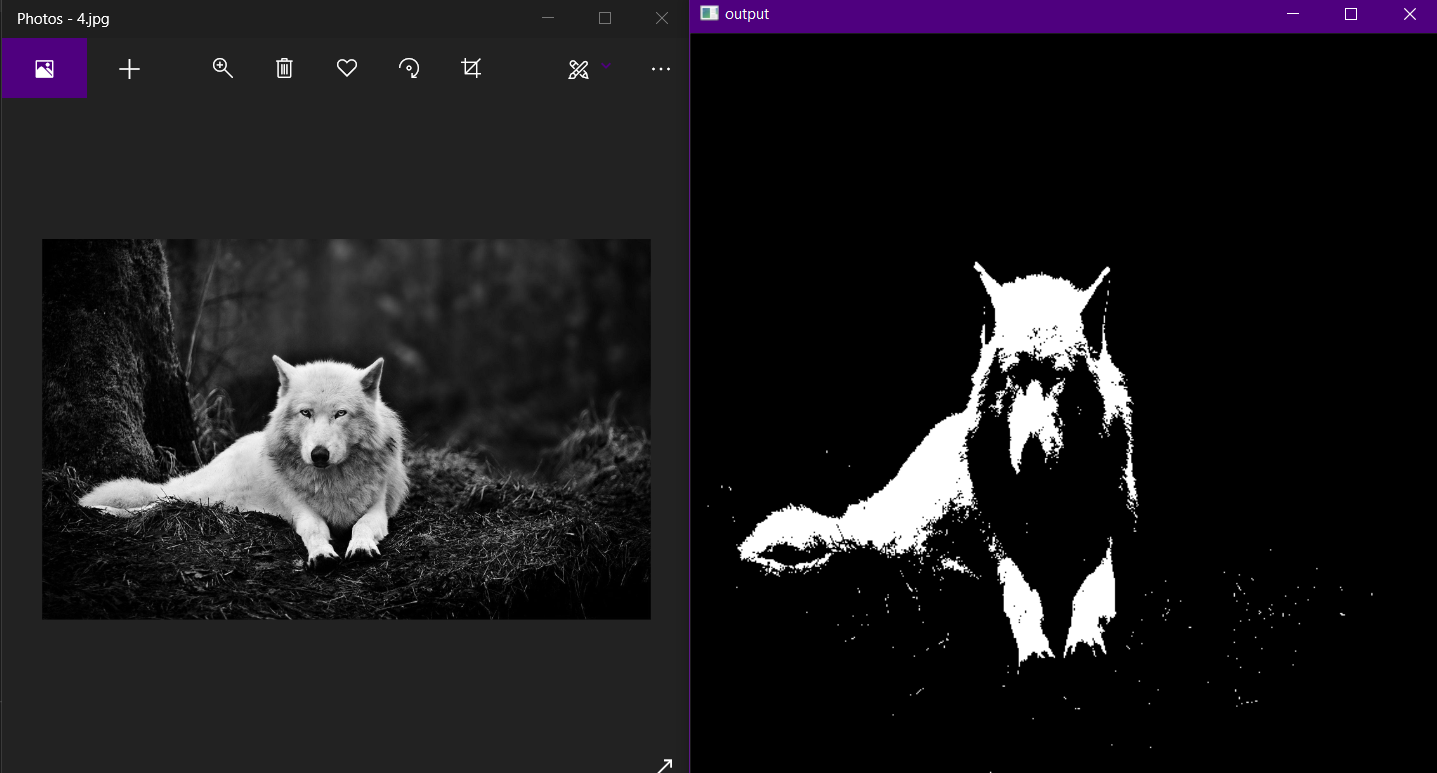
12 |
13 | # assignment_3
14 | 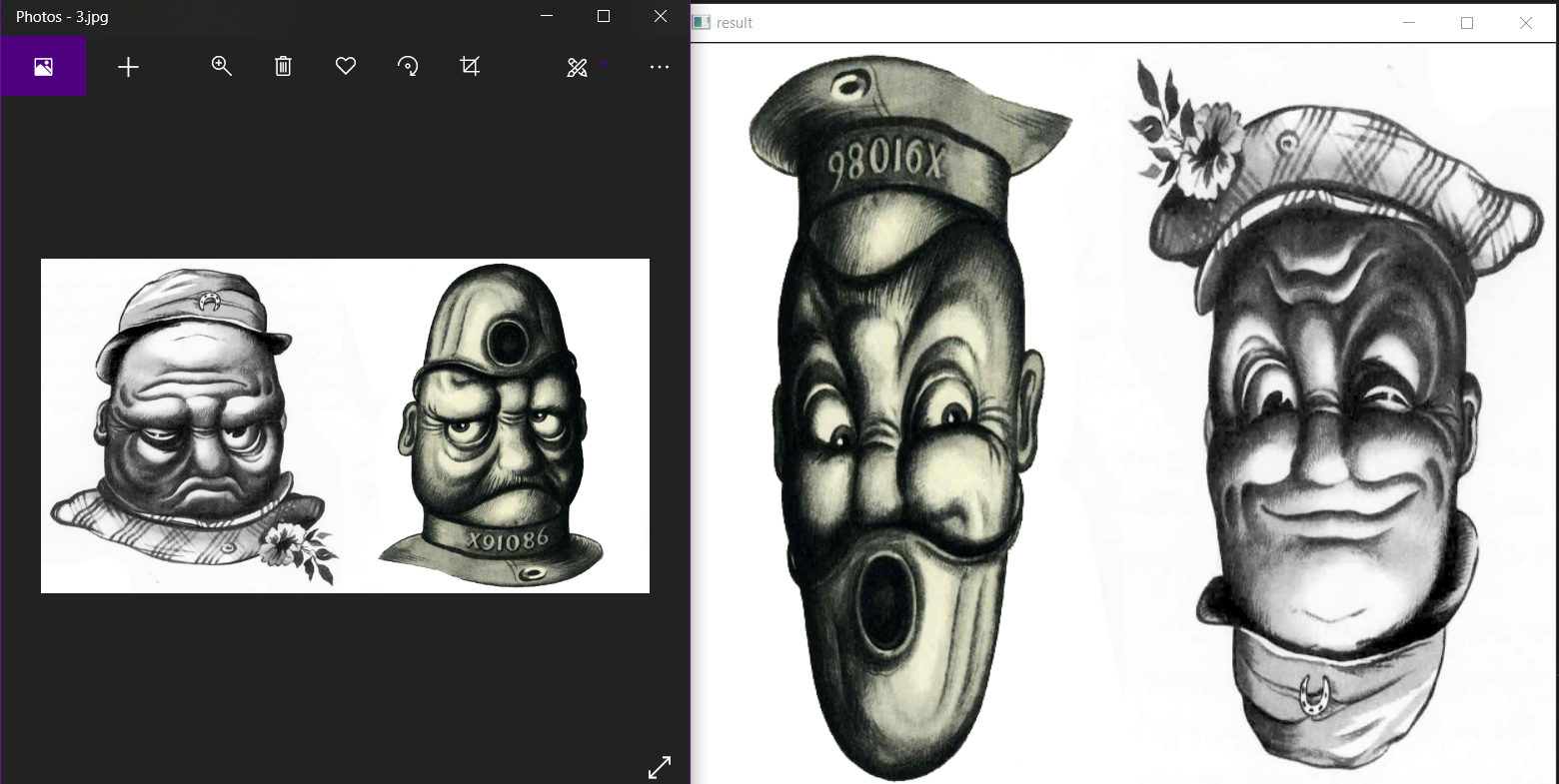
15 |
16 | # assignment_2
17 | 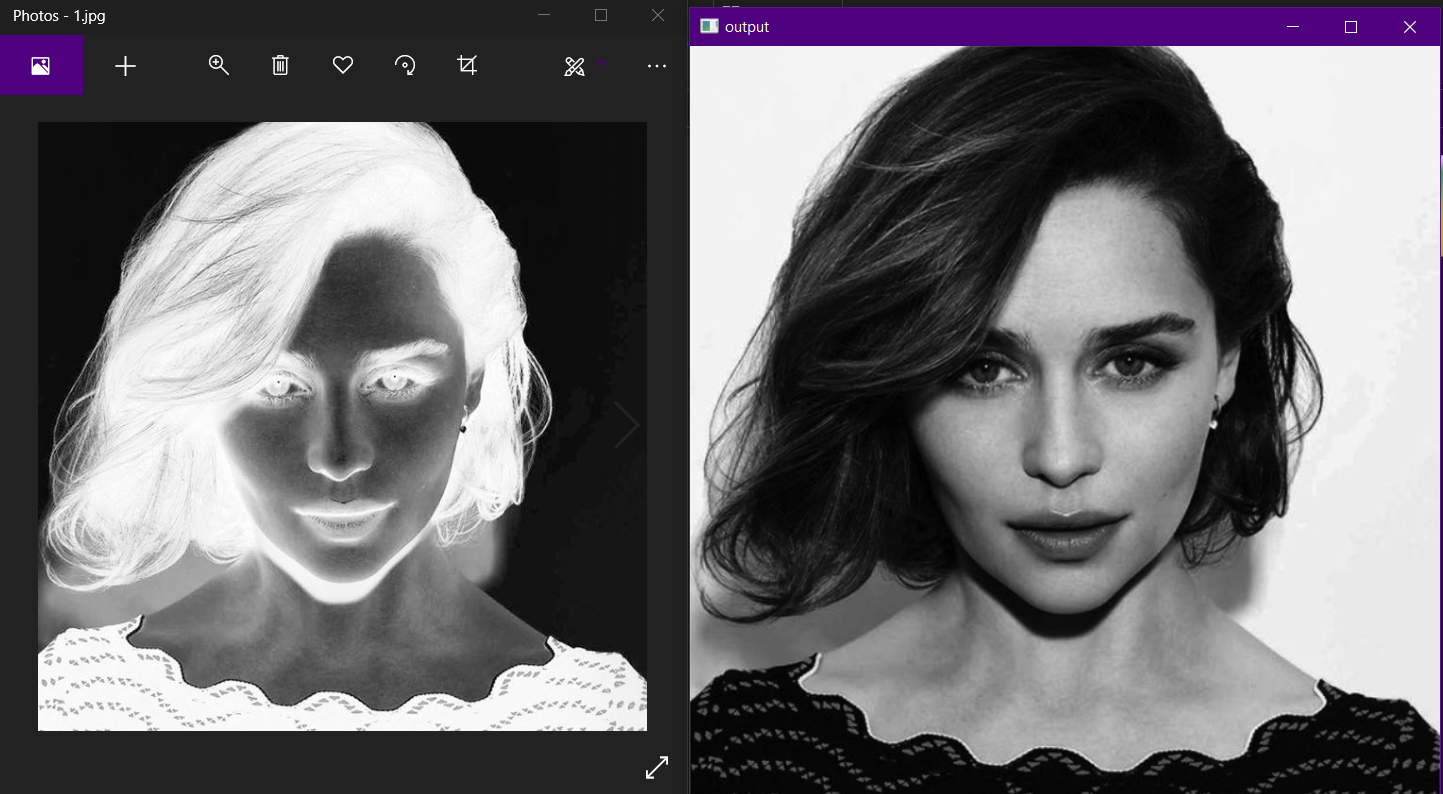
18 |
19 | # assignment_1
20 | 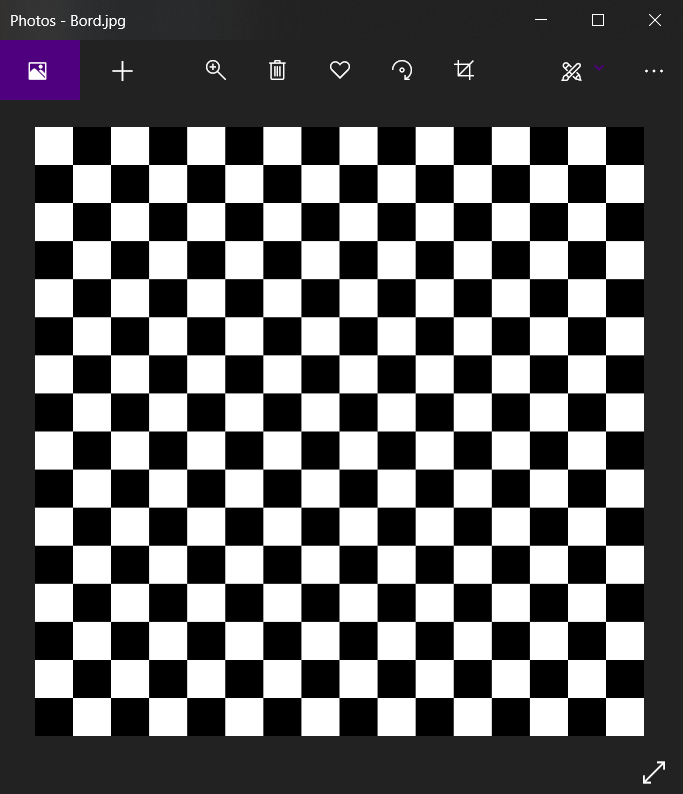
21 |
--------------------------------------------------------------------------------
/lesson9/README.md:
--------------------------------------------------------------------------------
1 | # lesson-29
2 | ## rubik
3 | 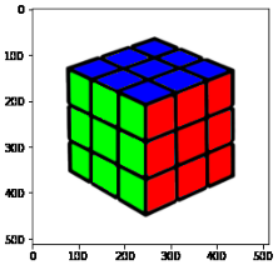
4 | ## green carrot
5 | 
6 | 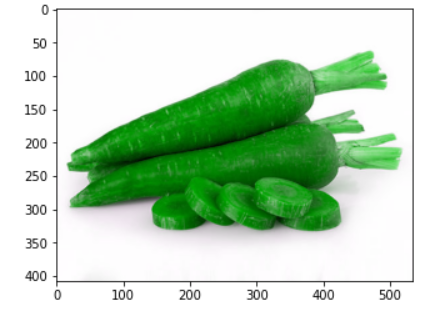
7 | ## microsoft logo
8 | 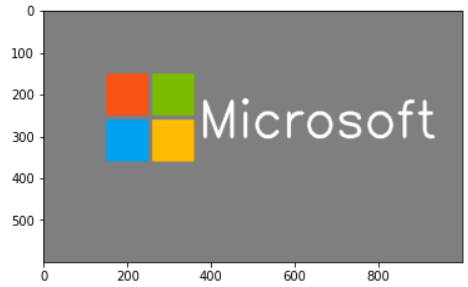
9 | ## color piker
10 | 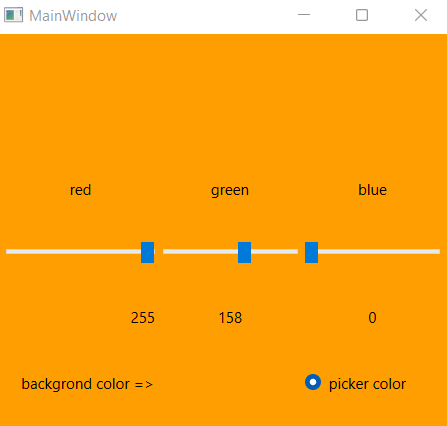
11 | 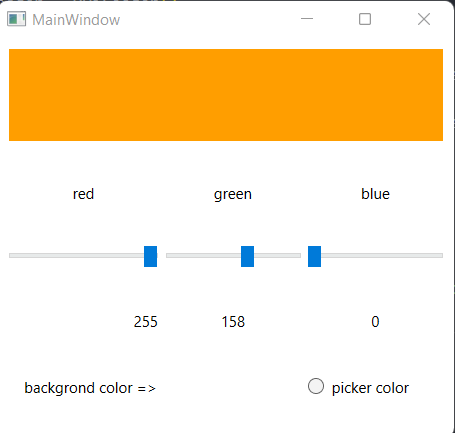
12 | ## color scan
13 | https://user-images.githubusercontent.com/88095232/190715393-1ad6b4f8-8137-414d-b726-b0c69440e2d8.mp4
14 |
--------------------------------------------------------------------------------
/lesson5/README.md:
--------------------------------------------------------------------------------
1 |
2 |
3 | https://user-images.githubusercontent.com/88095232/144674522-1f714415-7516-4813-95e4-8ff95054e5f4.mp4
4 |
5 | 
6 | 
7 | 
8 | 
9 | 
10 | 
11 | 
12 | 
13 |
14 |
--------------------------------------------------------------------------------
/lesson2/README.md:
--------------------------------------------------------------------------------
1 | tamrin1
2 | 
3 | tamrin2
4 | 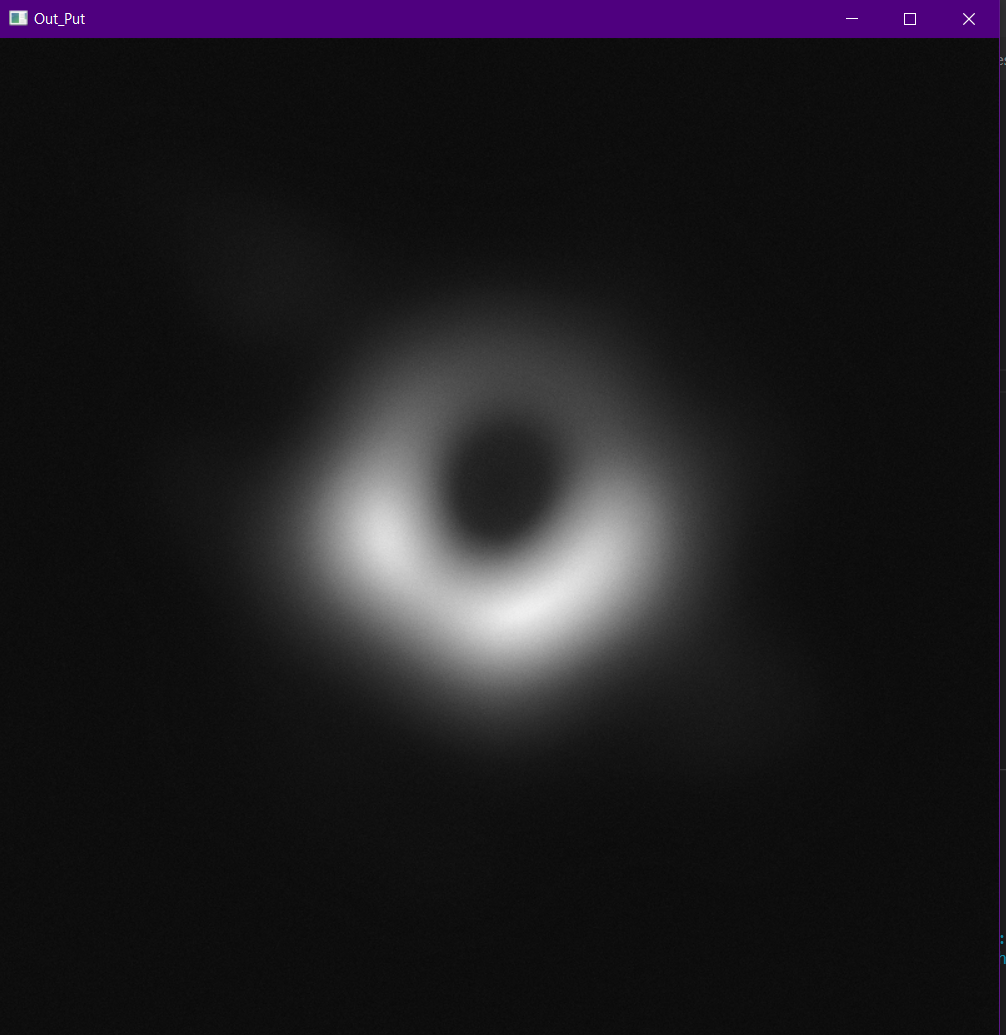
5 | tamrin3
6 | 
7 | 
8 | tamrin4
9 | 
10 | tamrin5
11 | 
12 | tamrin6
13 | 
14 | tamrin7
15 | 
16 |
17 |
18 |
--------------------------------------------------------------------------------
/lesson5/tamrin5.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import cv2
3 |
4 | video_cap = cv2.VideoCapture(0)
5 | size_text = 1.5
6 | while True:
7 | ret,frame = video_cap.read()
8 |
9 | frame = cv2.cvtColor(frame,cv2.COLOR_BGR2GRAY)
10 |
11 | me = frame[200:300,300:400]
12 |
13 | if ret == False:
14 | break
15 |
16 | camera_filter = np.ones((35,35))/1225
17 | frame = cv2.filter2D(frame,-1,camera_filter)
18 |
19 | frame[200:300,300:400] = me
20 | color_me = frame[200:300,300:400]
21 |
22 | if 0 < np.average(color_me) <= 85:
23 | cv2.rectangle(frame,(300,200), (400,300), (0, 0, 0),2)
24 | cv2.putText(frame,'Black',(50,50),cv2.FONT_HERSHEY_SIMPLEX,1,(0,0,0),int(size_text))
25 | size_text += 0.1
26 | elif 85 < np.average(color_me) <= 170:
27 | cv2.rectangle(frame,(300,200), (400,300), (127, 127, 127),2)
28 | cv2.putText(frame,'gray',(50,50),cv2.FONT_HERSHEY_SIMPLEX,1,(127,127,127),int(size_text))
29 | size_text == 2.5
30 | elif 170 < np.average(color_me) <= 255:
31 | cv2.rectangle(frame,(300,200), (400,300), (255, 255, 255),2)
32 | cv2.putText(frame,'white',(50,50),cv2.FONT_HERSHEY_SIMPLEX,1,(255, 255, 255),int(size_text))
33 | size_text -= 0.1
34 | cv2.imshow('Camera',frame)
35 | cv2.waitKey(1)
--------------------------------------------------------------------------------
/lesson8/sudoku.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | import numpy as np
3 | import matplotlib.pyplot as plt
4 | import argparse
5 | parser = argparse.ArgumentParser(description="yasin sudoku detector")
6 |
7 | parser.add_argument("--input", type=str, help="path of your input image")
8 | parser.add_argument("--filter_siz", type=int, help="size of GaussianBlur mask",default=7)
9 | parser.add_argument("--output", type=str, help="path of your output image")
10 |
11 | args = parser.parse_args()
12 |
13 | img = cv2.imread(args.input)
14 | img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
15 |
16 | img_blurred = cv2.GaussianBlur(img_gray, (args.filter_siz, args.filter_siz), 3)
17 | thresh = cv2.adaptiveThreshold(img_blurred, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY, 11, 2)
18 | thresh = cv2.bitwise_not(thresh)
19 |
20 | contours = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
21 | contours = contours[0]
22 | contours = sorted(contours, key=cv2.contourArea, reverse= True)
23 |
24 | sudoku_contour = None
25 |
26 | for contour in contours:
27 | epsilon = 0.02 * cv2.arcLength(contour, True)
28 | approx = cv2.approxPolyDP(contour, epsilon, True)
29 |
30 | if len(approx) == 4:
31 | sudoku_contour = approx
32 | break
33 | if sudoku_contour is None:
34 | print("I can not find Sudoku ")
35 | else:
36 | result = cv2.drawContours(img, [sudoku_contour], -1, (0, 255, 255), 20)
37 | plt.imshow(result)
38 | cv2.imwrite(args.output, result)
39 |
--------------------------------------------------------------------------------
/lesson9/color_scan.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | import numpy as np
3 |
4 |
5 | cam = cv2.VideoCapture(0)
6 |
7 | while True:
8 | _, frame = cam.read()
9 | frame = cv2.resize(frame, (800, 800))
10 | width, height, _ = frame.shape
11 | blur = cv2.blur(frame,(50,50))
12 | rectangle = frame[300:500,300:500]
13 | blur[300:500,300:500] = rectangle
14 |
15 | R = int(np.mean(rectangle[:,:,2]))
16 | G = int(np.mean(rectangle[:,:,1]))
17 | B = int(np.mean(rectangle[:,:,0]))
18 |
19 | if 150 < R <= 255 and 150 < G <= 255 and 150 < B <= 255:
20 | rgb_color = "White"
21 | elif 0 <= R <= 100 and 0 <= G <= 100 and 0 <= B <= 100:
22 | rgb_color = "Black"
23 | elif 101 <= R <= 149 and 101 <= G <= 149 and 101 <= B <= 149:
24 | rgb_color = "Gray"
25 | elif 0 <= R <= 100 and 0 <= G <= 100 and 100 <= B <= 255:
26 | rgb_color = "Blue"
27 | elif 100 <= R <= 200 and 0 <= G <= 100 and 0 <= B <= 100:
28 | rgb_color = "Red"
29 | elif 0 <= R <= 50 and 100 <= G <= 150 and 0 <= B <= 150:
30 | rgb_color = "Green"
31 | elif 90 <= R <= 150 and 90 <= G <= 150 and 120 <= B <= 200:
32 | rgb_color = "Magenta"
33 | elif 100 <= R <= 255 and 100 <= G <= 255 and 0 <= B <= 100:
34 | rgb_color = "Yellow"
35 | elif 0 <= R <= 100 and 100 <= G <= 150 and 100 <= B <= 200:
36 | rgb_color = "Cyan"
37 |
38 | cv2.putText(blur,f"R: {str(R)}, G: {str(G)}, B: {str(B)}",(10,40),cv2.FONT_HERSHEY_SCRIPT_COMPLEX,1,(G,R,B),2)
39 | cv2.putText(blur,f"Color: {rgb_color}",(10,70),cv2.FONT_HERSHEY_SCRIPT_COMPLEX,1,(B,G,R),2)
40 | cv2.imshow("frame", blur)
41 | if cv2.waitKey(1) & 0xFF==ord("q"):
42 | break
43 |
44 | cam.release()
45 | cv2.destroyAllWindows()
46 |
--------------------------------------------------------------------------------
/lesson6/25.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import cv2
3 | video_cap = cv2.VideoCapture(0)
4 | size_text = 1.5
5 |
6 | while True:
7 | ret, frame = video_cap.read()
8 | if not ret:
9 | break
10 | frame_gray = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
11 | width, height = frame_gray.shape
12 |
13 | target = frame_gray[(width//8)*3:(width//8)*5, (height//8)*3:(height//8)*5]
14 |
15 | kernel = np.ones((45, 45), np.float32)/2025
16 | frame_gray = cv2.filter2D(frame_gray, -1, kernel, borderType=cv2.BORDER_CONSTANT)
17 |
18 | alpha = -3
19 | beta = -100
20 | enhanced_target = cv2.convertScaleAbs(target, alpha=alpha, beta=beta)
21 |
22 | frame_gray[(width//8)*3:(width//8)*5, (height//8)*3:(height//8)*5] = enhanced_target
23 | cv2.rectangle(frame_gray, (height//8*3, width//8*3), ((height//8*5), (width//8*5)), (0, 0, 0), 4)
24 | color_me = np.average(enhanced_target)
25 | if size_text <= 0:
26 | break
27 | if 0 < np.average(color_me) <= 85:
28 | cv2.rectangle(frame,(300,200), (400,300), (0, 0, 0),2)
29 | cv2.putText(frame,'Black',(50,50),cv2.FONT_HERSHEY_SIMPLEX,1,(0,0,0),int(size_text))
30 | size_text += 0.1
31 | elif 85 < np.average(color_me) <= 170:
32 | cv2.rectangle(frame,(300,200), (400,300), (127, 127, 127),2)
33 | cv2.putText(frame,'gray',(50,50),cv2.FONT_HERSHEY_SIMPLEX,1,(127,127,127),int(size_text))
34 | size_text == 2.5
35 | elif 170 < np.average(color_me) <= 255:
36 | cv2.rectangle(frame,(300,200), (400,300), (255, 255, 255),2)
37 | cv2.putText(frame,'white',(50,50),cv2.FONT_HERSHEY_SIMPLEX,1,(255, 255, 255),int(size_text))
38 | size_text -= 0.1
39 | cv2.imshow("cam-0", frame_gray)
40 |
41 | video_cap.release()
42 | cv2.destroyAllWindows()
43 |
--------------------------------------------------------------------------------
/lesson8/sudoku_live.py:
--------------------------------------------------------------------------------
1 | import argparse
2 | import cv2
3 | import numpy as np
4 | import matplotlib.pyplot as plt
5 | from imutils.perspective import four_point_transform
6 |
7 | parser = argparse.ArgumentParser(description='yasin sudoku detector')
8 | parser.add_argument('--filter_siz', type=int, help='size of GaussianBlur mask', default=7)
9 | args = parser.parse_args()
10 |
11 | video = cv2.VideoCapture(0)
12 |
13 | while True:
14 |
15 | ret, frame = video.read()
16 |
17 | if not ret:
18 | break
19 |
20 | frame = cv2.cvtColor(frame, cv2.COLOR_BGR2GRAY)
21 |
22 | thresh = cv2.GaussianBlur(frame, (args.filter_siz, args.filter_siz), 3)
23 | thresh = cv2.adaptiveThreshold(thresh, 255, cv2.ADAPTIVE_THRESH_GAUSSIAN_C, cv2.THRESH_BINARY, 11, 2)
24 |
25 | contours = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
26 | contours = contours[0]
27 | contours = sorted(contours, key=cv2.contourArea, reverse=True)
28 |
29 | sudoku_contour = None
30 |
31 | for contour in contours:
32 | epsilon = 0.02 * cv2.arcLength(contour, True)
33 | approx = cv2.approxPolyDP(contour, epsilon, True)
34 |
35 | if len(approx) == 4:
36 | sudoku_contour = approx
37 | break
38 |
39 | if sudoku_contour is None:
40 | print("I can not find Sudoku ")
41 | else:
42 | cv2.drawContours(frame, [sudoku_contour], -1, (0, 255, 255), 20)
43 | crop = four_point_transform(frame, approx.reshape(4,2))
44 | crop = cv2.resize(crop, (500, 500))
45 | cv2.imshow('result', frame)
46 | if cv2.waitKey(1) == ord('s'):
47 | cv2.imwrite("sudoku.jpg", crop)
48 |
49 | if cv2.waitKey(1) == ord('q'):
50 | break
51 |
52 | video.release()
53 | cv2.destroyAllWindows()
54 |
--------------------------------------------------------------------------------
/lesson9/main_color_picker.py:
--------------------------------------------------------------------------------
1 | from PySide6.QtWidgets import *
2 | from PySide6.QtUiTools import *
3 | from PySide6.QtCore import *
4 |
5 | class Color_Picker(QMainWindow):
6 | def __init__(self):
7 | super().__init__()
8 |
9 | loader = QUiLoader()
10 | self.ui = loader.load("form.ui", None)
11 | self.ui.show()
12 | self.ui.sliderblue.valueChanged.connect(self.Blue)
13 | self.ui.sliderred.valueChanged.connect(self.Red)
14 | self.ui.slidergreen.valueChanged.connect(self.Green)
15 | self.ui.green_color_number.setText("0")
16 | self.ui.red_color_number.setText("0")
17 | self.ui.blue_color_number.setText("0")
18 | def Blue(self):
19 | value=str(self.ui.sliderblue.value())
20 | self.ui.blue_color_number.setText(value)
21 | self.ui.rgb_color.setStyleSheet(f'background-color:rgb({self.ui.sliderred.value()},{self.ui.slidergreen.value()},{value})')
22 | self.Background_color()
23 | def Red(self):
24 | value=str(self.ui.sliderred.value())
25 | self.ui.red_color_number.setText(value)
26 | self.ui.rgb_color.setStyleSheet(f'background-color:rgb({value},{self.ui.slidergreen.value()},{self.ui.sliderblue.value()})')
27 | self.Background_color()
28 | def Green(self):
29 | value = str(self.ui.slidergreen.value())
30 | self.ui.green_color_number.setText(value)
31 | self.ui.rgb_color.setStyleSheet(f'background-color:rgb({self.ui.sliderred.value()},{value},{self.ui.sliderblue.value()})')
32 | self.Background_color()
33 | def Background_color(self):
34 | if self.ui.rgb_btn.isChecked():
35 | self.ui.setStyleSheet(f'background-color:rgb({self.ui.red_color_number.text()},{self.ui.green_color_number.text()},{self.ui.blue_color_number.text()})')
36 | else:
37 | self.ui.setStyleSheet("background-color: rgb(255, 255, 255)")
38 |
39 | app = QApplication()
40 | window = Color_Picker()
41 | app.exec_()
--------------------------------------------------------------------------------
/lesson6/tamrin 1.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | import cvzone
3 | import keyboard
4 |
5 |
6 | f_detector = cv2.CascadeClassifier("haarcascade_frontalface_default.xml")
7 | e_detector = cv2.CascadeClassifier("haarcascade_eye.xml")
8 | s_detector = cv2.CascadeClassifier("haarcascade_smile.xml")
9 | f_emoj = cv2.imread("glass.png", cv2.IMREAD_UNCHANGED)
10 | e_Emoj = cv2.imread("eye.png", cv2.IMREAD_UNCHANGED)
11 | s_Emoj = cv2.imread("smile.png", cv2.IMREAD_UNCHANGED)
12 |
13 | video_cap = cv2.VideoCapture(0)
14 | current_state = 0
15 | while True:
16 | ret, frame = video_cap.read()
17 | if ret == False:
18 | break
19 |
20 | cv2.putText(frame, "^_^", (10, 50), cv2.FONT_HERSHEY_SIMPLEX, 2, (0, 255, 0), 3)
21 |
22 | k = cv2.waitKey(1)
23 | if keyboard.is_pressed('1'):
24 | FACES = f_detector.detectMultiScale(frame, 1.3)
25 | for (x, y, w, h) in FACES:
26 | finalEmojy = cv2.resize(f_emoj, (w, h))
27 | frame = cvzone.overlayPNG(frame, finalEmojy, [x, y])
28 |
29 | if keyboard.is_pressed('2'):
30 | LEYE = e_detector.detectMultiScale(frame, 2, maxSize=(50,50))
31 | for (x, y, w, h) in LEYE:
32 | finalEmojy = cv2.resize(e_Emoj, (w, h))
33 | frame = cvzone.overlayPNG(frame, finalEmojy, [x, y])
34 | SMILE = s_detector.detectMultiScale(frame, 1.3, 15)
35 | for (x, y, w, h) in SMILE:
36 | finalEmojy = cv2.resize(s_Emoj, (w, h))
37 | frame = cvzone.overlayPNG(frame, finalEmojy, [x, y])
38 |
39 | if keyboard.is_pressed('3'):
40 | FACES = f_detector.detectMultiScale(frame, 1.3)
41 | for (x, y, w, h) in FACES:
42 | blurred = frame[y:y+h, x:x+w]
43 | pixlated = cv2.resize(blurred, (15, 15), interpolation=cv2.INTER_LINEAR)
44 | output = cv2.blur(pixlated[y:y+h, x:x+h],(30,30))
45 | # frame[y:y+h, x:x+w] = output
46 |
47 | if keyboard.is_pressed('4'):
48 | FACES = f_detector.detectMultiScale(frame, 1.3)
49 | for (x, y, w, h) in FACES:
50 | blurred = cv2.GaussianBlur(frame[y:y+h, x:x+w], (25, 25), 35)
51 | frame[y:y+h, x:x+w] = blurred
52 |
53 | if keyboard.is_pressed('esc'):
54 | exit()
55 |
56 | cv2.imshow("Out_Put", frame)
57 |
--------------------------------------------------------------------------------
/lesson3/projeckt_main.py:
--------------------------------------------------------------------------------
1 | import cv2
2 | import cvzone
3 | import keyboard
4 |
5 |
6 | f_detector = cv2.CascadeClassifier("haarcascade_frontalface_default.xml")
7 | e_detector = cv2.CascadeClassifier("haarcascade_eye.xml")
8 | s_detector = cv2.CascadeClassifier("haarcascade_smile.xml")
9 | f_emoj = cv2.imread("glass.png", cv2.IMREAD_UNCHANGED)
10 | e_Emoj = cv2.imread("eye.png", cv2.IMREAD_UNCHANGED)
11 | s_Emoj = cv2.imread("smile.png", cv2.IMREAD_UNCHANGED)
12 |
13 | video_cap = cv2.VideoCapture(0)
14 | current_state = 0
15 | while True:
16 | ret, frame = video_cap.read()
17 | if ret == False:
18 | break
19 |
20 | cv2.putText(frame, "^_^", (10, 50), cv2.FONT_HERSHEY_SIMPLEX, 2, (0, 255, 0), 3)
21 |
22 | k = cv2.waitKey(1)
23 | if keyboard.is_pressed('1'):
24 | FACES = f_detector.detectMultiScale(frame, 1.3)
25 | for (x, y, w, h) in FACES:
26 | finalEmojy = cv2.resize(f_emoj, (w, h))
27 | frame = cvzone.overlayPNG(frame, finalEmojy, [x, y])
28 |
29 | if keyboard.is_pressed('2'):
30 | LEYE = e_detector.detectMultiScale(frame, 2, maxSize=(50,50))
31 | for (x, y, w, h) in LEYE:
32 | finalEmojy = cv2.resize(e_Emoj, (w, h))
33 | frame = cvzone.overlayPNG(frame, finalEmojy, [x, y])
34 | SMILE = s_detector.detectMultiScale(frame, 1.3, 15)
35 | for (x, y, w, h) in SMILE:
36 | finalEmojy = cv2.resize(s_Emoj, (w, h))
37 | frame = cvzone.overlayPNG(frame, finalEmojy, [x, y])
38 |
39 | if keyboard.is_pressed('3'):
40 | FACES = f_detector.detectMultiScale(frame, 1.3)
41 | for (x, y, w, h) in FACES:
42 | blurred = frame[y:y+h, x:x+w]
43 | pixlated = cv2.resize(blurred, (15, 15), interpolation=cv2.INTER_LINEAR)
44 | output = cv2.resize(pixlated, (w, h), interpolation=cv2.INTER_NEAREST)
45 | frame[y:y+h, x:x+w] = output
46 |
47 | if keyboard.is_pressed('4'):
48 | FACES = f_detector.detectMultiScale(frame, 1.3)
49 | for (x, y, w, h) in FACES:
50 | blurred = cv2.GaussianBlur(frame[y:y+h, x:x+w], (25, 25), 35)
51 | frame[y:y+h, x:x+w] = blurred
52 |
53 | if keyboard.is_pressed('esc'):
54 | exit()
55 |
56 | cv2.imshow("Out_Put", frame)
57 |
--------------------------------------------------------------------------------
/lesson6/crop_image.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 24,
6 | "id": "8526e3f1-6837-4465-b3eb-b627b9e51490",
7 | "metadata": {},
8 | "outputs": [],
9 | "source": [
10 | "import os\n",
11 | "import cv2\n",
12 | "import numpy as np\n",
13 | "import matplotlib.pyplot as plt\n",
14 | "img = cv2.imread('img/mnist.png', 0)"
15 | ]
16 | },
17 | {
18 | "cell_type": "code",
19 | "execution_count": 25,
20 | "id": "7dad4fa6-5d5d-4ccf-9e7b-77d69134e764",
21 | "metadata": {},
22 | "outputs": [
23 | {
24 | "name": "stdout",
25 | "output_type": "stream",
26 | "text": [
27 | "Folders already exists.\n",
28 | "Folders already exists.\n",
29 | "Folders already exists.\n",
30 | "Folders already exists.\n",
31 | "Folders already exists.\n",
32 | "Folders already exists.\n",
33 | "Folders already exists.\n",
34 | "Folders already exists.\n",
35 | "Folders already exists.\n",
36 | "Folders already exists.\n"
37 | ]
38 | }
39 | ],
40 | "source": [
41 | "for i in range(1, 11):\n",
42 | " try:\n",
43 | " os.mkdir(f'output/{i}')\n",
44 | " except FileExistsError:\n",
45 | " print('Folders already exists.')"
46 | ]
47 | },
48 | {
49 | "cell_type": "code",
50 | "execution_count": 26,
51 | "id": "b9c2ebfe-86f4-4cf3-9f56-29354d4c4089",
52 | "metadata": {},
53 | "outputs": [],
54 | "source": [
55 | "rows, cols = img.shape\n",
56 | "for index, i in enumerate(range(0, rows, 20)):\n",
57 | " for j in range(0, cols, 20):\n",
58 | " folder_number = index//5\n",
59 | " small_img = img[i:i+20, j:j+20]\n",
60 | " cv2.imwrite(f'output/{folder_number}/{i}{j}.jpg', small_img)"
61 | ]
62 | },
63 | {
64 | "cell_type": "code",
65 | "execution_count": null,
66 | "id": "96405351-59fd-42d9-b6d8-5673ed6d9f05",
67 | "metadata": {},
68 | "outputs": [],
69 | "source": []
70 | }
71 | ],
72 | "metadata": {
73 | "kernelspec": {
74 | "display_name": "Python 3 (ipykernel)",
75 | "language": "python",
76 | "name": "python3"
77 | },
78 | "language_info": {
79 | "codemirror_mode": {
80 | "name": "ipython",
81 | "version": 3
82 | },
83 | "file_extension": ".py",
84 | "mimetype": "text/x-python",
85 | "name": "python",
86 | "nbconvert_exporter": "python",
87 | "pygments_lexer": "ipython3",
88 | "version": "3.7.9"
89 | }
90 | },
91 | "nbformat": 4,
92 | "nbformat_minor": 5
93 | }
94 |
--------------------------------------------------------------------------------
/lesson6/gift_sonw.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 44,
6 | "id": "c05f9fd8-06a8-4ac2-80dd-c3c6b7887b2e",
7 | "metadata": {},
8 | "outputs": [],
9 | "source": [
10 | "import random\n",
11 | "import cv2\n",
12 | "import numpy as np\n",
13 | "import matplotlib.pyplot as plt\n",
14 | "from cvzone import overlayPNG\n",
15 | "import imageio"
16 | ]
17 | },
18 | {
19 | "cell_type": "code",
20 | "execution_count": 45,
21 | "id": "b0f281cf-2c9e-4d5f-aa50-be28695ce2fe",
22 | "metadata": {},
23 | "outputs": [],
24 | "source": [
25 | "background_img = cv2.imread('img/street_snow.jpg')\n",
26 | "snows = []\n",
27 | "s_size = random.randint(1, 10)\n",
28 | "for i in range(3):\n",
29 | " snow_img = cv2.imread('img/snow.png', -1)\n",
30 | " small_snow = cv2.resize(snow_img, (s_size , s_size))\n",
31 | " snows.append(small_snow)"
32 | ]
33 | },
34 | {
35 | "cell_type": "code",
36 | "execution_count": 46,
37 | "id": "d397ca9e-87fc-4a42-ace7-4cae53bd6c60",
38 | "metadata": {},
39 | "outputs": [],
40 | "source": [
41 | "y, x, _ = background_img.shape\n",
42 | "snows_positoins = [] \n",
43 | "for i in range(200): \n",
44 | " temp_x = random.choice(range(50, x-s_size))\n",
45 | " temp_y = random.choice(range(50, y-s_size))\n",
46 | " snows_positoins.append([temp_y, temp_x])"
47 | ]
48 | },
49 | {
50 | "cell_type": "code",
51 | "execution_count": 47,
52 | "id": "a5031e09-a254-4cbe-80d3-f033dd9c4d49",
53 | "metadata": {},
54 | "outputs": [],
55 | "source": [
56 | "with imageio.get_writer(\"snow.gif\", mode=\"I\") as writer:\n",
57 | " for i in range(200):\n",
58 | " frame = background_img\n",
59 | " for j in range(200):\n",
60 | " frame = overlayPNG(frame, snows[j % 3], (snows_positoins[j][1], snows_positoins[j][0])) \n",
61 | " snows_positoins[j][0] += 4\n",
62 | " rnd_x = random.choices([1, 2, -1], weights=[5,55,55])[0]\n",
63 | " snows_positoins[j][1] += rnd_x\n",
64 | " if snows_positoins[j][0] < 0 or snows_positoins[j][0] + s_size >= y or snows_positoins[j][1] < 0 or snows_positoins[j][1] + s_size >= x:\n",
65 | " snows_positoins[j][0] = 0\n",
66 | " snows_positoins[j][1] = random.randint(0, x - s_size - 1)\n",
67 | " "
68 | ]
69 | }
70 | ],
71 | "metadata": {
72 | "kernelspec": {
73 | "display_name": "Python 3 (ipykernel)",
74 | "language": "python",
75 | "name": "python3"
76 | },
77 | "language_info": {
78 | "codemirror_mode": {
79 | "name": "ipython",
80 | "version": 3
81 | },
82 | "file_extension": ".py",
83 | "mimetype": "text/x-python",
84 | "name": "python",
85 | "nbconvert_exporter": "python",
86 | "pygments_lexer": "ipython3",
87 | "version": "3.7.9"
88 | }
89 | },
90 | "nbformat": 4,
91 | "nbformat_minor": 5
92 | }
93 |
--------------------------------------------------------------------------------
/lesson9/form.ui:
--------------------------------------------------------------------------------
1 |
2 |
3 | MainWindow
4 |
5 |
6 |
7 | 0
8 | 0
9 | 365
10 | 319
11 |
12 |
13 |
14 | MainWindow
15 |
16 |
17 |
18 | -
19 |
20 |
21 | border-bottom-color: rgb(0, 0, 0);
22 |
23 |
24 |
25 |
26 |
27 |
28 | -
29 |
30 |
31 | blue
32 |
33 |
34 | Qt::AlignCenter
35 |
36 |
37 |
38 | -
39 |
40 |
41 | 255
42 |
43 |
44 | Qt::Horizontal
45 |
46 |
47 |
48 | -
49 |
50 |
51 | 255
52 |
53 |
54 | Qt::Horizontal
55 |
56 |
57 |
58 | -
59 |
60 |
61 |
62 |
63 |
64 | Qt::AlignCenter
65 |
66 |
67 |
68 | -
69 |
70 |
71 |
72 |
73 |
74 | Qt::AlignCenter
75 |
76 |
77 |
78 | -
79 |
80 |
81 | 255
82 |
83 |
84 | Qt::Horizontal
85 |
86 |
87 |
88 | -
89 |
90 |
91 | picker color
92 |
93 |
94 |
95 | -
96 |
97 |
98 | green
99 |
100 |
101 | Qt::AlignCenter
102 |
103 |
104 |
105 | -
106 |
107 |
108 | red
109 |
110 |
111 | Qt::AlignCenter
112 |
113 |
114 |
115 | -
116 |
117 |
118 | backgrond color =>
119 |
120 |
121 |
122 | -
123 |
124 |
125 |
126 |
127 |
128 | Qt::AlignRight|Qt::AlignTrailing|Qt::AlignVCenter
129 |
130 |
131 |
132 |
133 |
134 |
144 |
145 |
146 |
147 |
148 |
149 |
--------------------------------------------------------------------------------
/lesson4/TFLiteFaceDetector.py:
--------------------------------------------------------------------------------
1 | from functools import partial
2 | import cv2
3 | import tensorflow as tf
4 | import numpy as np
5 |
6 |
7 | class UltraLightFaceDetecion():
8 | def __init__(self, filepath, input_size=(320, 240), conf_threshold=0.6,
9 | center_variance=0.1, size_variance=0.2,
10 | nms_max_output_size=200, nms_iou_threshold=0.3) -> None:
11 |
12 | self._feature_maps = np.array([[40, 30], [20, 15], [10, 8], [5, 4]])
13 | self._min_boxes = [[10, 16, 24], [32, 48], [64, 96], [128, 192, 256]]
14 |
15 | self._resize = partial(cv2.resize, dsize=input_size)
16 | self._input_size = np.array(input_size)[:, None]
17 |
18 | self._anchors_xy, self._anchors_wh = self._generate_anchors()
19 | self._conf_threshold = conf_threshold
20 | self._center_variance = center_variance
21 | self._size_variance = size_variance
22 | self._nms = partial(tf.image.non_max_suppression,
23 | max_output_size=nms_max_output_size,
24 | iou_threshold=nms_iou_threshold)
25 |
26 | # tflite model init
27 | self._interpreter = tf.lite.Interpreter(model_path=filepath)
28 | self._interpreter.allocate_tensors()
29 |
30 | # model details
31 | input_details = self._interpreter.get_input_details()
32 | output_details = self._interpreter.get_output_details()
33 |
34 | # inference helper
35 | self._set_input_tensor = partial(self._interpreter.set_tensor,
36 | input_details[0]["index"])
37 | self._get_boxes_tensor = partial(self._interpreter.get_tensor,
38 | output_details[0]["index"])
39 | self._get_scores_tensor = partial(self._interpreter.get_tensor,
40 | output_details[1]["index"])
41 |
42 | def _generate_anchors(self):
43 | anchors = []
44 | for feature_map_w_h, min_box in zip(self._feature_maps, self._min_boxes):
45 |
46 | wh_grid = min_box / self._input_size
47 | wh_grid = np.tile(wh_grid.T, (np.prod(feature_map_w_h), 1))
48 |
49 | xy_grid = np.meshgrid(range(feature_map_w_h[0]),
50 | range(feature_map_w_h[1]))
51 | xy_grid = np.add(xy_grid, 0.5)
52 |
53 | xy_grid /= feature_map_w_h[..., None, None]
54 |
55 | xy_grid = np.stack(xy_grid, axis=-1)
56 | xy_grid = np.tile(xy_grid, [1, 1, len(min_box)])
57 | xy_grid = xy_grid.reshape(-1, 2)
58 |
59 | prior = np.concatenate((xy_grid, wh_grid), axis=-1)
60 | anchors.append(prior)
61 |
62 | anchors = np.concatenate(anchors, axis=0)
63 | anchors = np.clip(anchors, 0.0, 1.0)
64 |
65 | return anchors[:, :2], anchors[:, 2:]
66 |
67 | def _pre_processing(self, img):
68 | resized = self._resize(img)
69 | image_rgb = resized[..., ::-1]
70 | image_norm = image_rgb.astype(np.float32)
71 | cv2.normalize(image_norm, image_norm,
72 | alpha=-1, beta=1, norm_type=cv2.NORM_MINMAX)
73 | return image_norm[None, ...]
74 |
75 | def inference(self, img):
76 | # BGR image to tensor
77 | input_tensor = self._pre_processing(img)
78 |
79 | # set tensor and invoke
80 | self._set_input_tensor(input_tensor)
81 | self._interpreter.invoke()
82 |
83 | # get results
84 | boxes = self._get_boxes_tensor()[0]
85 | scores = self._get_scores_tensor()[0]
86 |
87 | # decode boxes to corner format
88 | boxes, scores = self._post_processing(boxes, scores)
89 | boxes *= np.tile(img.shape[1::-1], 2)
90 |
91 | return boxes, scores
92 |
93 | def _post_processing(self, boxes, scores):
94 | # bounding box regression
95 | boxes = self._decode_regression(boxes)
96 | scores = scores[:, 1]
97 |
98 | # confidence threshold filter
99 | conf_mask = self._conf_threshold < scores
100 | boxes, scores = boxes[conf_mask], scores[conf_mask]
101 |
102 | # non-maximum suppression
103 | nms_mask = self._nms(boxes=boxes, scores=scores)
104 | boxes = np.take(boxes, nms_mask, axis=0)
105 |
106 | return boxes, scores
107 |
108 | def _decode_regression(self, reg):
109 | # bounding box regression
110 | center_xy = reg[:, :2] * self._center_variance * \
111 | self._anchors_wh + self._anchors_xy
112 | center_wh = np.exp(
113 | reg[:, 2:] * self._size_variance) * self._anchors_wh / 2
114 |
115 | # center to corner
116 | start_xy = center_xy - center_wh
117 | end_xy = center_xy + center_wh
118 |
119 | boxes = np.concatenate((start_xy, end_xy), axis=-1)
120 | boxes = np.clip(boxes, 0.0, 1.0)
121 |
122 | return boxes
123 |
124 |
125 | if __name__ == '__main__':
126 | import sys
127 | import time
128 |
129 | fd = UltraLightFaceDetecion("weights/RFB-320.tflite",
130 | conf_threshold=0.88)
131 |
132 | cap = cv2.VideoCapture(sys.argv[1])
133 | color = (125, 255, 125)
134 |
135 | while True:
136 | ret, frame = cap.read()
137 |
138 | if not ret:
139 | break
140 |
141 | start_time = time.perf_counter()
142 | boxes, scores = fd.inference(frame)
143 | print(time.perf_counter() - start_time)
144 |
145 | for det in boxes.astype(np.int32):
146 | cv2.rectangle(frame, (det[0], det[1]),
147 | (det[2], det[3]), (2, 255, 0), 1)
148 |
149 | cv2.imshow("result", frame)
150 | if cv2.waitKey(1) == ord('q'):
151 | break
152 |
--------------------------------------------------------------------------------
/lesson4/TFLiteFaceAlignment.py:
--------------------------------------------------------------------------------
1 | import numpy as np
2 | import cv2
3 | from numpy.ma.core import left_shift
4 | import tensorflow as tf
5 | from functools import partial
6 | from TFLiteFaceDetector import UltraLightFaceDetecion
7 | import sys
8 |
9 | #left_eye = 35,36,33,37,39,42,40,41
10 | #righ_eye = 89,90,87,91,93,96,94,95
11 | #lips = 52,55,56,53,59,58,61,68,67,71 63,64
12 |
13 |
14 | class CoordinateAlignmentModel():
15 | def __init__(self, filepath, marker_nums=106, input_size=(192, 192)):
16 | self._marker_nums = marker_nums
17 | self._input_shape = input_size
18 | self._trans_distance = self._input_shape[-1] / 2.0
19 |
20 | self.eye_bound = ([35, 41, 40, 42, 39, 37, 33, 36],
21 | [89, 95, 94, 96, 93, 91, 87, 90])
22 |
23 | # tflite model init
24 | self._interpreter = tf.lite.Interpreter(model_path=filepath)
25 | self._interpreter.allocate_tensors()
26 |
27 | # model details
28 | input_details = self._interpreter.get_input_details()
29 | output_details = self._interpreter.get_output_details()
30 |
31 | # inference helper
32 | self._set_input_tensor = partial(self._interpreter.set_tensor,
33 | input_details[0]["index"])
34 | self._get_output_tensor = partial(self._interpreter.get_tensor,
35 | output_details[0]["index"])
36 |
37 | self.pre_landmarks = None
38 |
39 | def _calibrate(self, pred, thd, skip=6):
40 | if self.pre_landmarks is not None:
41 | for i in range(pred.shape[0]):
42 | if abs(self.pre_landmarks[i, 0] - pred[i, 0]) > skip:
43 | self.pre_landmarks[i, 0] = pred[i, 0]
44 | elif abs(self.pre_landmarks[i, 0] - pred[i, 0]) > thd:
45 | self.pre_landmarks[i, 0] += pred[i, 0]
46 | self.pre_landmarks[i, 0] /= 2
47 |
48 | if abs(self.pre_landmarks[i, 1] - pred[i, 1]) > skip:
49 | self.pre_landmarks[i, 1] = pred[i, 1]
50 | elif abs(self.pre_landmarks[i, 1] - pred[i, 1]) > thd:
51 | self.pre_landmarks[i, 1] += pred[i, 1]
52 | self.pre_landmarks[i, 1] /= 2
53 | else:
54 | self.pre_landmarks = pred
55 |
56 | def _preprocessing(self, img, bbox, factor=3.0):
57 |
58 | maximum_edge = max(bbox[2:4] - bbox[:2]) * factor
59 | scale = self._trans_distance * 4.0 / maximum_edge
60 | center = (bbox[2:4] + bbox[:2]) / 2.0
61 | cx, cy = self._trans_distance - scale * center
62 |
63 | M = np.array([[scale, 0, cx], [0, scale, cy]])
64 |
65 | cropped = cv2.warpAffine(img, M, self._input_shape, borderValue=0.0)
66 | inp = cropped[..., ::-1].astype(np.float32)
67 |
68 | return inp[None, ...], M
69 |
70 | def _inference(self, input_tensor):
71 | self._set_input_tensor(input_tensor)
72 | self._interpreter.invoke()
73 |
74 | return self._get_output_tensor()[0]
75 |
76 | def _postprocessing(self, out, M):
77 | iM = cv2.invertAffineTransform(M)
78 | col = np.ones((self._marker_nums, 1))
79 |
80 | out = out.reshape((self._marker_nums, 2))
81 |
82 | out += 1
83 | out *= self._trans_distance
84 |
85 | out = np.concatenate((out, col), axis=1)
86 |
87 | return out @ iM.T # dot product
88 |
89 | def get_landmarks(self, image, detected_faces=None):
90 |
91 | for box in detected_faces:
92 | inp, M = self._preprocessing(image, box)
93 | out = self._inference(inp)
94 | pred = self._postprocessing(out, M)
95 |
96 | # self._calibrate(pred, 1, skip=6)
97 | # yield self.pre_landmarks
98 |
99 | yield pred
100 |
101 |
102 | def warp_effect(frame,landmark,num1,num2):
103 |
104 | x = min(landmark[:,0])
105 | x_max = max(landmark[:,0])
106 | y = min(landmark[:,1])
107 | y_max = max(landmark[:,1])
108 | w = x_max-x
109 | h = y_max-y
110 | median_x = (x+x_max)//2
111 | median_y = (y+y_max)//2
112 |
113 | mask = np.zeros(frame.shape,np.uint8)
114 | cv2.drawContours(mask,[landmark],-1,(255,255,255),-1)
115 | img_resize = cv2.resize(frame,(0,0),fx=num2,fy=num2)
116 | img_resize=img_resize / 255
117 | mask_resize = cv2.resize(mask,(0,0),fx=num2,fy=num2)
118 | mask_resize=mask_resize / 255
119 | image = frame[int(median_y - (num1*h)):int(median_y+(num1*h)),int(median_x-(num1*w)):int(median_x+(num1*w))]
120 | image=image / 255
121 | try:
122 | forground = cv2.multiply(mask_resize,img_resize)
123 | background = cv2.multiply(image,1-mask_resize[y*num2:(y+h)*num2,x*num2:(x+w)*num2])
124 | resualt = cv2.add(background,forground[y*num2:(y+h)*num2,x*num2:(x+w)*num2])
125 | resualt = resualt*255
126 | frame[int(median_y - (num1*h)):int(median_y+(num1*h)),int(median_x-(num1*w)):int(median_x+(num1*w))]= resualt
127 | except:
128 | pass
129 |
130 | # ---------> ((y_min+y_max)/2) -/+ h |2x
131 | # ---------> ((x_min+x_max)/2) -/+ w |2x
132 |
133 | # ---------> ((y_min+y_max)/2) -/+ 2*h |4x
134 | # ---------> ((x_min+x_max)/2) -/+ 2*w |4x
135 |
136 | # ---------> ((y_min+y_max)/2) -/+ 1.5*h |3x
137 | # ---------> ((x_min+x_max)/2) -/+ 1.5*w |3x
138 |
139 | return frame
140 |
141 |
142 | if __name__ == '__main__':
143 | fd = UltraLightFaceDetecion("weights/RFB-320.tflite",conf_threshold=0.88)
144 | fa = CoordinateAlignmentModel("weights/coor_2d106.tflite")
145 |
146 |
147 | cap = cv2.VideoCapture(0)
148 | format = cv2.VideoWriter_fourcc(*"XVID")
149 | save = cv2.VideoWriter("video.mp4",format,20.0,(640, 480))
150 | while True:
151 | ret , frame = cap.read()
152 | boxes, scores = fd.inference(frame)
153 |
154 | for pred in fa.get_landmarks(frame, boxes):
155 | pred_int = np.round(pred).astype(np.int)
156 |
157 | eye_left = [35,36,33,37,39,42,40,41]
158 | landmark_left_eye = []
159 | for i in eye_left:
160 | landmark_left_eye.append(tuple(pred_int[i]))
161 |
162 | eye_right = [89,90,87,91,93,96,94,95]
163 | landmark_right_eye = []
164 | for i in eye_right:
165 | landmark_right_eye.append(tuple(pred_int[i]))
166 |
167 |
168 | lips = [52,55,56,53,59,58,61,68,67,71,63,64]
169 | landmark_lips = []
170 | for i in lips:
171 | landmark_lips.append(tuple(pred_int[i]))
172 |
173 | landmark_left_eye = np.array(landmark_left_eye)
174 | landmark_right_eye = np.array(landmark_right_eye)
175 | landmark_lips = np.array(landmark_lips)
176 |
177 | # for i,p in enumerate(np.round(pred).astype(np.int)):
178 | # cv2.circle(img, tuple(p), 1, (125, 255, 125), 1, cv2.LINE_AA)
179 | # cv2.putText(img,str(i),tuple(p),cv2.FONT_HERSHEY_COMPLEX,0.25,(0,0,255),1)
180 | # print(i,p)
181 |
182 | _,y1 = pred_int[60]
183 | _,y2 = pred_int[62]
184 |
185 | warp_effect(frame,landmark_left_eye,1,2)
186 | warp_effect(frame,landmark_right_eye,1,2)
187 | if 5 <= y1-y2 <=15:
188 | warp_effect(frame,landmark_lips,1,2)
189 | if 16<= y1-y2 <=27:
190 | warp_effect(frame,landmark_lips,1.5,3)
191 | if 28<= y1-y2:
192 | warp_effect(frame,landmark_lips,2,4)
193 | save.write(frame)
194 | cv2.imshow("Face warp effect",frame)
195 | if cv2.waitKey(1) & 0xFF==ord("0"):
196 | break
197 |
198 | cap.release()
199 | save.release()
200 | cv2.destroyAllWindows()
201 |
--------------------------------------------------------------------------------
/lesson9/logo_microsoft.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 19,
6 | "id": "8ab728fd-a811-4b21-b144-3087df6cc001",
7 | "metadata": {},
8 | "outputs": [],
9 | "source": [
10 | "import cv2 \n",
11 | "import matplotlib.pyplot as plt\n",
12 | "import numpy as np"
13 | ]
14 | },
15 | {
16 | "cell_type": "code",
17 | "execution_count": 31,
18 | "id": "b4f4fad1-b4d6-476d-9142-d8574d3b5c8b",
19 | "metadata": {},
20 | "outputs": [
21 | {
22 | "data": {
23 | "text/plain": [
24 | ""
25 | ]
26 | },
27 | "execution_count": 31,
28 | "metadata": {},
29 | "output_type": "execute_result"
30 | },
31 | {
32 | "data": {
33 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAADsCAYAAACPFubKAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/MnkTPAAAACXBIWXMAAAsTAAALEwEAmpwYAAAOY0lEQVR4nO3cXYxd1XnG8f9TDx910mK+avlLhShWI1QpQC1klFyk0LRAo5gLEoGiYiFLc0NV0kRKTXtRIfUiSFVIkCpUK6R1ojQJJUmxEEpKDVHVixCGQvkyhAkJsS2DEwJO2lHa0ry9OMv44IyZsefMHLPm/5OOzlrvWmfO2nv2PN6zZx+nqpAk9eVXxr0ASdLoGe6S1CHDXZI6ZLhLUocMd0nqkOEuSR1alHBPckWSZ5NMJ9m+GO8hSTq2jPo+9yQrgO8C7wf2AQ8D11XV0yN9I0nSMS3GmfslwHRVPV9V/wN8GdiyCO8jSTqGxQj3dcDeof6+VpMkLZGJcb1xkklgEuCUU075nXPOOWdcS5Gkt6QDBw78uKrOnW1sMcJ9P7BhqL++1d6gqnYAOwDWrl1bk5OTi7AUSerXLbfc8sKxxhbjsszDwMYk5yc5FbgW2LUI7yNJOoaRn7lX1WtJ/hj4JrAC+FxVPTXq95EkHduiXHOvqvuA+xbja0uS5uYnVCWpQ4a7JHXIcJekDhnuktQhw12SOmS4S1KHDHdJ6pDhLkkdMtwlqUOGuyR1yHCXpA4Z7pLUIcNdkjpkuEtShwx3SeqQ4S5JHTLcJalDhrskdchwl6QOGe6S1CHDXZI6ZLhLUocMd0nqkOEuSR0y3CWpQ3OGe5LPJTmY5Mmh2llJ7k/yXHs+s9WT5PYk00keT3LxYi5ekjS7+Zy5/z1wxVG17cDuqtoI7G59gCuBje0xCdwxmmVKko7HnOFeVf8K/OSo8hZgZ2vvBK4eqn++Br4NrEqyZkRrlSTN04lec19dVQda+0VgdWuvA/YOzdvXapKkJbTgP6hWVQF1vK9LMplkKsnUzMzMQpchSRpyouH+0uHLLe35YKvvBzYMzVvfar+kqnZU1aaq2rRy5coTXIYkaTYnGu67gK2tvRW4Z6h+fbtrZjNwaOjyjSRpiUzMNSHJl4D3Aeck2Qf8JfBJ4K4k24AXgA+36fcBVwHTwAxwwyKsWZI0hznDvaquO8bQ5bPMLeDGhS5KkrQwfkJVkjpkuEtShwx3SeqQ4S5JHTLcJalDhrskdchwl6QOGe6S1CHDXZI6ZLhLUocMd0nqkOEuSR0y3CWpQ4a7JHXIcJekDhnuktQhw12SOmS4S1KHDHdJ6pDhLkkdMtwlqUOGuyR1yHCXpA4Z7pLUoTnDPcmGJA8meTrJU0luavWzktyf5Ln2fGarJ8ntSaaTPJ7k4sXeCEnSG83nzP014ONVdQGwGbgxyQXAdmB3VW0Edrc+wJXAxvaYBO4Y+aolSW9qznCvqgNV9e+t/TNgD7AO2ALsbNN2Ale39hbg8zXwbWBVkjWjXrgk6diO65p7kvOAi4CHgNVVdaANvQisbu11wN6hl+1rNUnSEpl3uCd5O/BV4KNV9dPhsaoqoI7njZNMJplKMjUzM3M8L5UkzWFe4Z7kFAbB/sWq+lorv3T4ckt7Ptjq+4ENQy9f32pvUFU7qmpTVW1auXLlia5fkjSL+dwtE+BOYE9VfWpoaBewtbW3AvcM1a9vd81sBg4NXb6RJC2BiXnMeQ/wR8ATSR5rtT8HPgnclWQb8ALw4TZ2H3AVMA3MADeMcsGSpLnNGe5V9W9AjjF8+SzzC7hxgeuSJC2An1CVpA4Z7pLUIcNdkjpkuEtShwx3SeqQ4S5JHTLcJalDhrskdchwl6QOGe6S1CHDXZI6ZLhLUocMd0nqkOEuSR0y3CWpQ4a7JHXIcJekDhnuktQhw12SOmS4S1KHDHdJ6pDhLkkdMtwlqUOGuyR1yHCXpA7NGe5JTk/ynST/keSpJLe0+vlJHkoyneQrSU5t9dNaf7qNn7fI2yBJOsp8ztz/G7isqt4NXAhckWQzcCtwW1W9E3gF2NbmbwNeafXb2jxJ0hKaM9xr4D9b95T2KOAy4O5W3wlc3dpbWp82fnmSjGrBkqS5zeuae5IVSR4DDgL3A98DXq2q19qUfcC61l4H7AVo44eAs0e4ZknSHOYV7lX1f1V1IbAeuAR410LfOMlkkqkkUzMzMwv9cpKkIcd1t0xVvQo8CFwKrEoy0YbWA/tbez+wAaCNnwG8PMvX2lFVm6pq08qVK09s9ZKkWc3nbplzk6xq7V8F3g/sYRDy17RpW4F7WntX69PGH6iqGuGaJUlzmJh7CmuAnUlWMPjH4K6qujfJ08CXk/wV8ChwZ5t/J/CFJNPAT4BrF2HdkqQ3MWe4V9XjwEWz1J9ncP396PrPgQ+NZHWSpBPiJ1QlqUOGuyR1yHCXpA4Z7pLUIcNdkjpkuEtShwx3SeqQ4S5JHTLcJalDhrskdchwl6QOGe6S1CHDXZI6ZLhLUocMd0nqkOEuSR0y3CWpQ4a7JHXIcJekDhnuktQhw12SOmS4S1KHDHdJ6pDhLkkdmne4J1mR5NEk97b++UkeSjKd5CtJTm3101p/uo2ft0hrlyQdw/Gcud8E7Bnq3wrcVlXvBF4BtrX6NuCVVr+tzZMkLaF5hXuS9cAfAp9t/QCXAXe3KTuBq1t7S+vTxi9v8yVJS2S+Z+6fBj4B/KL1zwZerarXWn8fsK611wF7Adr4oTZfkrRE5gz3JB8ADlbVI6N84ySTSaaSTM3MzIzyS0vSsjcxjznvAT6Y5CrgdODXgc8Aq5JMtLPz9cD+Nn8/sAHYl2QCOAN4+egvWlU7gB0Aa9eurYVuiCTpiDnP3Kvq5qpaX1XnAdcCD1TVR4AHgWvatK3APa29q/Vp4w9UleEtSUtoIfe5/xnwsSTTDK6p39nqdwJnt/rHgO0LW6Ik6XjN57LM66rqW8C3Wvt54JJZ5vwc+NAI1iZJOkF+QlWSOmS4S1KHDHdJ6pDhLkkdMtwlqUOGuyR1yHCXpA4Z7pLUIcNdkjpkuEtShwx3SeqQ4S5JHTLcJalDhrskdchwl6QOGe6S1CHDXZI6ZLhLUocMd0nqkOEuSR0y3CWpQ4a7JHXIcJekDhnuktQhw12SOjSvcE/ygyRPJHksyVSrnZXk/iTPteczWz1Jbk8yneTxJBcv5gZIkn7Z8Zy5/25VXVhVm1p/O7C7qjYCu1sf4EpgY3tMAneMarGSpPlZyGWZLcDO1t4JXD1U/3wNfBtYlWTNAt5HknSc5hvuBfxzkkeSTLba6qo60NovAqtbex2wd+i1+1rtDZJMJplKMjUzM3MCS5ckHcvEPOe9t6r2J/kN4P4kzwwPVlUlqeN546raAewAWLt27XG9VpL05uZ15l5V+9vzQeDrwCXAS4cvt7Tng236fmDD0MvXt5okaYnMGe5J3pbk1w63gd8HngR2AVvbtK3APa29C7i+3TWzGTg0dPlGkrQE5nNZZjXw9SSH5/9DVX0jycPAXUm2AS8AH27z7wOuAqaBGeCGka9akvSm5gz3qnoeePcs9ZeBy2epF3DjSFYnSTohfkJVkjpkuEtShwx3SeqQ4S5JHTLcJalDhrskdchwl6QOGe6S1CHDXZI6ZLhLUocMd0nqkOEuSR0y3CWpQ4a7JHXIcJekDhnuktQhw12SOmS4S1KHDHdJ6pDhLkkdMtwlqUOGuyR1yHCXpA4Z7pLUIcNdkjpkuEtShwx3SeqQ4S5JHUpVjXsNJPkZ8Oy413GSOAf48bgXcZJwXxzhvjjCfXHEb1bVubMNTCz1So7h2araNO5FnAySTLkvBtwXR7gvjnBfzI+XZSSpQ4a7JHXoZAn3HeNewEnEfXGE++II98UR7ot5OCn+oCpJGq2T5cxdkjRCYw/3JFckeTbJdJLt417PYkuyIcmDSZ5O8lSSm1r9rCT3J3muPZ/Z6klye9s/jye5eLxbMFpJViR5NMm9rX9+kofa9n4lyamtflrrT7fx88a68BFLsirJ3UmeSbInyaXL+Jj40/az8WSSLyU5fbkeFwsx1nBPsgL4G+BK4ALguiQXjHNNS+A14ONVdQGwGbixbfN2YHdVbQR2tz4M9s3G9pgE7lj6JS+qm4A9Q/1bgduq6p3AK8C2Vt8GvNLqt7V5PfkM8I2qehfwbgb7ZNkdE0nWAX8CbKqq3wZWANeyfI+LE1dVY3sAlwLfHOrfDNw8zjWNYR/cA7yfwYe41rTaGgb3/gP8LXDd0PzX573VH8B6BqF1GXAvEAYfTpk4+vgAvglc2toTbV7GvQ0j2g9nAN8/enuW6TGxDtgLnNW+z/cCf7Acj4uFPsZ9WebwN/Kwfa22LLRfIS8CHgJWV9WBNvQisLq1e95HnwY+Afyi9c8GXq2q11p/eFtf3w9t/FCb34PzgR8Bf9cuUX02ydtYhsdEVe0H/hr4IXCAwff5EZbncbEg4w73ZSvJ24GvAh+tqp8Oj9XgNKTr25iSfAA4WFWPjHstJ4EJ4GLgjqq6CPgvjlyCAZbHMQHQ/q6whcE/eGuBtwFXjHVRb1HjDvf9wIah/vpW61qSUxgE+xer6mut/FKSNW18DXCw1XvdR+8BPpjkB8CXGVya+QywKsnh/xZjeFtf3w9t/Azg5aVc8CLaB+yrqoda/24GYb/cjgmA3wO+X1U/qqr/Bb7G4FhZjsfFgow73B8GNra/hJ/K4A8nu8a8pkWVJMCdwJ6q+tTQ0C5ga2tvZXAt/nD9+naHxGbg0NCv6m9ZVXVzVa2vqvMYfN8fqKqPAA8C17RpR++Hw/vnmja/izPZqnoR2Jvkt1rpcuBpltkx0fwQ2JxkZftZObwvlt1xsWDjvugPXAV8F/ge8BfjXs8SbO97Gfx6/TjwWHtcxeA64W7gOeBfgLPa/DC4o+h7wBMM7iIY+3aMeJ+8D7i3td8BfAeYBv4ROK3VT2/96Tb+jnGve8T74EJgqh0X/wScuVyPCeAW4BngSeALwGnL9bhYyMNPqEpSh8Z9WUaStAgMd0nqkOEuSR0y3CWpQ4a7JHXIcJekDhnuktQhw12SOvT/GUIrsE5vZKAAAAAASUVORK5CYII=\n",
34 | "text/plain": [
35 | ""
36 | ]
37 | },
38 | "metadata": {
39 | "needs_background": "light"
40 | },
41 | "output_type": "display_data"
42 | }
43 | ],
44 | "source": [
45 | "logo = np.ones((600, 1000, 3), dtype = \"uint8\") * 127\n",
46 | "plt.imshow(logo)"
47 | ]
48 | },
49 | {
50 | "cell_type": "code",
51 | "execution_count": 32,
52 | "id": "5ff372c8-38d6-44fb-a7c4-df0a4c2f9ad4",
53 | "metadata": {},
54 | "outputs": [],
55 | "source": [
56 | "logo[150:250, 150:250] = (246, 83, 20)\n",
57 | "\n",
58 | "logo[260:360, 150:250] = (0, 161, 241)\n",
59 | "\n",
60 | "logo[150:250, 260:360] = (124, 187, 0)\n",
61 | "\n",
62 | "logo[260:360, 260:360] = (255, 187, 0)\n"
63 | ]
64 | },
65 | {
66 | "cell_type": "code",
67 | "execution_count": 33,
68 | "id": "0f6d7470-7cb2-49c8-b19a-5a7f52bd6772",
69 | "metadata": {},
70 | "outputs": [
71 | {
72 | "data": {
73 | "text/plain": [
74 | ""
75 | ]
76 | },
77 | "execution_count": 33,
78 | "metadata": {},
79 | "output_type": "execute_result"
80 | },
81 | {
82 | "data": {
83 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAXcAAADsCAYAAACPFubKAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/MnkTPAAAACXBIWXMAAAsTAAALEwEAmpwYAAAkjUlEQVR4nO3daXBV553n8e9fV0JoRwuLBEICJMDGYRUxdGgSQwxeYuOY4E6ma0J1uYqqqUxNerqrup2Zqpl21bzorprqTKemKzOuLHa60502jh2wO14xaZMawIjF7EICjCSQBBKSEFrQ9swLnXu4Ai1XG1c++n0ole55zjn3Pvdw9LvnPuc5zzHnHCIiEixxsa6AiIiMP4W7iEgAKdxFRAJI4S4iEkAKdxGRAFK4i4gE0ISEu5k9YWZlZlZhZi9NxGuIiMjgbLz7uZtZCLgAPA5UA0eA7zjnzo7rC4mIyKAm4sj9y0CFc+6Sc64T+BWwbQJeR0REBjER4T4XqIqYrvbKRETkAYmP1Qub2S5gF0BCQsKanJycWFVFROQLqaampt45N3OgeRMR7leB/IjpeV5ZP865V4BXAPLy8tyuXbsmoCoiIsH18ssvXxls3kQ0yxwBis1sgZlNA74N7J2A1xERkUGM+5G7c67bzP4j8D4QAn7mnDsz3q8jIiKDm5A2d+fcb4HfTsRzi4jI8HSFqohIACncRUQCSOEuIhJACncRkQBSuIuIBJDCXUQkgBTuIiIBpHAXEQkghbuISAAp3EVEAkjhLiISQAp3EZEAUriLiASQwl1EJIAU7iIiAaRwFxEJIIW7iEgAKdxFRAJI4S4iEkAKdxGRAFK4i4gEkMJdRCSAFO4iIgGkcBcRCSCFu4hIAA0b7mb2MzO7bmanI8qyzOxDMyv3fmd65WZmPzKzCjM7aWarJ7LyIiIysGiO3F8Fnrin7CVgn3OuGNjnTQM8CRR7P7uAH49PNUVEZCSGDXfn3CfAzXuKtwGveY9fA56LKP+F63MImGFmueNUVxERidJo29xnO+dqvMe1wGzv8VygKmK5aq9MREQeoDGfUHXOOcCNdD0z22VmpWZW2tbWNtZqiIhIhNGGe124ucX7fd0rvwrkRyw3zyu7j3PuFedciXOuJDk5eZTVEBGRgYw23PcCO73HO4E9EeXf9XrNrAOaI5pvRETkAYkfbgEz+2fga0COmVUD/x34a+B1M3sRuAK84C3+W+ApoAJoA/5kAuosIiLDGDbcnXPfGWTW5gGWdcD3xlopEREZG12hKiISQAp3EZEAUriLiASQwl1EJIAU7iIiAaRwFxEJIIW7iEgAKdxFRAJI4S4iEkAKdxGRABp2+AGJkhvxqMcTyww38pGYJ4xhsa6CyJSicB9Hj9X+P2Z33IhpHeqmz2T/nD/om7AeXPFe3LSWmNbJbi7Grq2PaR1EphqF+zia3XGDgtYBh6+PDevFpVVDUmNs69GRFdvXF5mC1OYuIhJACncRkQBSuIuIBJDCXUQkgBTuIiIBpHAXEQkghbuISAAp3EVEAkjhLiISQAp3EZEAUriLiATQsOFuZvlmtt/MzprZGTP7vleeZWYfmlm59zvTKzcz+5GZVZjZSTNbPdFvQkRE+ovmyL0b+HPn3MPAOuB7ZvYw8BKwzzlXDOzzpgGeBIq9n13Aj8e91iIiMqRhw905V+OcO+Y9bgHOAXOBbcBr3mKvAc95j7cBv3B9DgEzzCx3vCsuIiKDG1Gbu5kVAquAw8Bs51yNN6sWmO09ngtURaxW7ZWJiMgDEnW4m1kq8GvgT51ztyLnOeccjOy2P2a2y8xKzay0ra1tJKuKiMgwogp3M0ugL9h/6Zx70yuuCze3eL+ve+VXgfyI1ed5Zf04515xzpU450qSk5NHW38RERlANL1lDPgpcM4597cRs/YCO73HO4E9EeXf9XrNrAOaI5pvRCadhIQEsrOzmT59eqyrIjJuornN3leAfw+cMrMTXtl/Af4aeN3MXgSuAC94834LPAVUAG3An4xnhSWYQqEQPT094/qccXFxOOdwQ9y8PC0tjW9+85vk5eVx+/Zt9u7dS2Vl5bjWQ75YEhISiI/vi8be3l7u3Lkz5PJ9x78MuZ/FwrDh7pz7PQx66/rNAyzvgO+NsV4yhTz88MOsWbOG0tJSzp07Ny7PmZGRweOPP05bWxsffvghXV1d9y0TFxfHM888w4IFCzAzEhMTef755/n5z39Oc3PzuNRDvjjS09NZvXo1RUVFZGRkYGbcuXOHgwcPUlpaOuA6iYmJbN26lbi4ON5//33a29sfcK0HpxtkS0wlJiayadMmcnJymDlzJpWVlbS2to75eb/yla+wbNkyent7uXTpEufPn79vmeTkZObMmeMfeZkZaWlp5OTkKNynmNWrV/PVr36V9PR0f38ASE1NZf369Zw+fZqOjo771nvooYdYuXIlZsbVq1c5cuTIg6z2kDT8gMRUQkICKSkpQN8f0tKlS8f8nOnp6SxZsgQzIxQKkZ6ePuBy7e3t3Lhxo9/X6ba2NhoaGsZcB/nimDlzJps3b/aP1p1zdHR00N7eTlNTE6WlpQMGO/Tta3FxcZjZoPtZrOjIXSaNuLg4Hn74YY4fP05vb++on6ewsDCqP7Senh727t3L9u3bmTNnDm1tbezdu5empqZRv7Z88RQVFRHusXf79m2OHj3KZ599RmdnJ729vXxRu2or3GVSmT9/PnPnzqWqqmr4hQcQHx/P2rVro16+ubmZX/7yl2RmZnLr1q0v7B+yjE4oFPK/5fX09LBnzx7Ky8tjXa1xoWYZmVTi4+NZsmTJqNfPyclh1qxZ/dpNh3Pnzh1qa2sV7FNQVlYWc+bMAeDmzZuB6imlcJdJxcwoLi4edZ/zJUuWMG3atHGulQRVUVERiYmJAFy8eHHYbo9fJAp3mXRmzpxJYWHhiNdLTExk+fLlIzpql6ltxowZ/v4StHMtCneZdOLi4njooYdGvN7cuXPJzMycgBqJfPHohKpMGuGrSePi4li0aBGZmZk0NjZGta6Z+f2NI58nGklJSSxZsoSqqqoRd4MMhUIUFBQwb948MjIy/PLOzk5u3LhBeXk5LS0tUT9feno6ixYtoqKiot96GRkZFBcXM3PmTP/qSYCqqirOnDkz4EVakdLS0vz1I5utmpqauHr1KleuXBn1FcJmRnJyMvn5+SxatKjfdu/s7KSsrIyampoxNXkkJiZSVFTE7Nmz/a6z0Nd1tba2loqKiqieP3wCddGiRQDk598dBmvZsmXMnDnTn66treXkyZP9nje8b4ZPwubm3h3NvLi4mMhxsurr6/nss89idi5H4S6TRltbG1VVVSxdupSUlBSKioqivigkLS2NRYsWYWbcunWLuro6iouLh13PzHjsscdYu3YtNTU1vPbaa1GFhJmxcOFC1q9fT2FhIaFQqF9zULjvfFNTE8eOHePYsWPDXpwVCoV45plnKCoq4ty5c7zxxhukpKRQUlLCqlWrSEtL8187bNWqVcTHxw96BWVKSgqrV69mzZo1/ofPvfXs6enh8uXLHDx4kMuXL0d9GX1iYiILFizgoYceYsGCBQPWzznHl7/8ZRobG7l48SLnzp2jqqoq6g+S+Ph4li1bxqOPPupfcHbv8zvnqKur49ChQ5w9e3bID7qioiK2b9/u902PlJ+f3y/snXOkpKTwu9/9rt8yL7zwAvHx8fetP2fOHP/kbHj9zMxM3n333ZgMTaBwl0nDOceZM2coLi4mFAqxZs0av7/xcJYvX+4fNV25ciXqo8RQKOQPPzBr1izS09O5cePGkOuYGSUlJWzZsmXAP/LwMgCZmZls2rSJRYsW8etf/3rIo/ikpCTmzp2LmTF//nxyc3N5+umnyc3NHfQ8Qnd396BHhmlpaWzfvp2CgoJB1zcz4uPjKSoqorCwkA8++IDS0tJhwygjI4Nt27axYMGCfu93oOcPhULk5OSQnZ1NSUkJJ06c4L333hv220Z8fDxbt25lzZo1g34LC4d9bm4u27ZtIz8/n/fff3/Q5+7o6KCzszOqE/bd3d33fSB3dHRw586dft+eBtPT00Nra2vMxpxRuI+juukzh1/oQdbBxWEt83B3MgZf4UFoy4l60atXr9LU1ER2djbZ2dnMmTNn2O5p4e6TZkZvby/nzp3zQ2e8RQZ7QkIC0BcClZWVnD9/3r/4Kisri+XLl5OSkoKZUVBQwPbt24cN+HBIhse5ycrK8puabt26xcmTJ/sNjVBbW8vVq/eNqH1fsDvnuH37NqdOneLmzZtAXxPD0qVLKSgoIBQKkZCQwJYtWwCGDfiSkhL/Q9E5R2trK9XV1Vy8eLHfBWjTpk1j8eLF5ObmMm3aNEKhECtXrqSiomLIcYQGCvY7d+5QVlbWb3+YP3++30MqLi6O1av7btk8WMBfuXKFV1991T9CX7Zsmb+vnD17lkuXLvnL1tfX37fv1dXV8eqrr/rbtbi42O+6W1FR0W+Yi8bGRj7//PNB3+NEU7iPo/1z/iDWVejPhbAL3xx01LfJqL29nRMnTrB582YSEhJYunTpsOE+a9YsZs2aBcD169epqKiYsHBfs2aNH+zh5oB9+/Zx+fJluru7+y175MgRHn30UdauXeu3zW/fvp3du3cP20QTHoYYoKuryx+86tatW0OuB31NMZHB3tPTw5EjRzh8+PB95zCOHTvGwoUL2bRpE7Nnz/YD3jk3aFPPjBkz+p3fOHr0KAcOHODWrVsDfiAcOnSIrKwsvvGNb1BYWEhcXBzr16+noqJiwAAOhUJs2bLFD3bnHBcuXOCTTz7h2rVr/V7j6NGj5ObmsnHjRpYsWdIv4N99990Bm3/q6uqoq6sD+npmhfeVysrKQd9zpPr6eurr64G+8YnC4V5TUxPV+g+KesuMF7PJ9QPYJPo3EuXl5f5YHo888ki/E2gDWblypX+SsKKiIqpmnNFIS0tj48aN/YL99ddfp7y8/L5gh74jtw8++IADBw7Q09PjH8GPpJtnV1cX+/btY//+/VEFO/S1w0cG+4EDB/jggw8GPDnd3d3NhQsX2L17N3V1dTjnSEhIYOPGjX4b+r3y8vL8/5OWlhb+7d/+jebm5kGP9Ht7e6mvr2f//v10dXVhZsycObPfCehI+fn5rF692g/2c+fO8dZbb3H16tX7XsM5x7Vr1/jNb37D2bNn/RPpK1eupKCgIKrtFVQK93HigG4L0WnxMf3ptlDE/Q4d8XFdJMR1xvQnZPcH31Dq6ur8r7OpqanMnz9/0GWnT5/un0gN98yYKIWFhaSmpgJ93xBef/11v4ljML29vXzyySccOHCAO3fucOfOnah7T/T09LBv3z4OHz4cdbttfHw8ixcv9puoDhw4wCeffDLsWD0NDQ3s3r3bP9+Qmpo6aDhGPle4OScaVVVVnDp1is7OThobG7l9+/aAyy1ZsoT4+Hicc5SVlbF3795BB+4K6+jo4O233+bcuXM458Z8pXMQqFlmHO3NeZzq6XkxrcO8jmt888Z7AMTHdfPHD/8TGYmxHb72dP0yPr5y39D/gwofrYW/Zq9YsYKysrIBA2rRokXMmDEDgOrq6gHbn8eDmbF06VLi4uLo7e3l97///bDBHhYO+DNnzhAXF8f169eHX4m+8w/RnNyMlJ2dzezZffeqv3HjBgcPHox6ELaGhgYOHDjA888/77fHnzlz5r7Xr6qqoqmpiaysLJKTk9m6dSsffvghDQ0NQ9a1t7eXd955h6NHj9Lc3DxgYCcmJvrdFDs7O/n444+HDfawjo4O9u/fz8KFC/0P/enTp0e9ftAo3MdRS3wqjQkzYlqHjO67X90NR0ZiM1lJ0fUVnygpCSPv53vx4kWamprIzMyksLCQzMzM+/qgmxmPPPKIH7ifffbZmEaTHErkN4jW1tYRnyjr7e0dthdOpPBR60DNPUMpLi7u10Q10r7lV65c4fbt26SlpTF//nxSU1PvOwHc2tpKaWkpjz/+OGbG4sWLyc/P58KFC5w7d46WlhZu3LhBT0/Pff8fvb29Q34A5+bmkpWVBfS1YY/0uoObN29SU1PDggULmDFjBnl5ef1Okk4lCneZlG7fvk1FRQUlJSUkJiayatUqPvroo37LzJ49m4ULF2JmtLS0UFFRMWH1KSgo8NuZwwE4kTo7O0f8fiKbZLq7u0fVRNXS0kJlZSXLli3zm2ZOnz5933InTpwgPz+fpUuX+hcxrVixghUrVtDT00NzczONjY1cv36dK1euUF9fz82bN4f9FhLZJHPhwoURX1jV09NDWVkZhYWFftOMwl1kkjl//jyrV68mFApRVFTEJ5980u9kaeRR6ueffz4ud3AaTFZWlt8lr7GxccL7Lnd1dUV9AjUsFAr5TVTd3d2jGivFOeefeI2Lixt0OIfw2PdXrlxh7dq1fpdN6PuQCXdlXbRoEevXr6e9vZ0zZ87w6aefUl9fP+j2C/cQAkZ905TI9SKfb6pRuMukVVlZybVr18jPzyc7O5vc3FyuXLkC9HUVDB+ldnV1TaouaFNFe3s7hw4d4uTJkyxZsoS5c+cye/ZssrOz/T7t4cBPTk6mpKSEZcuW8d5773Hq1KlJd0PpoFG4y6TV1dVFWVkZ8+bNIyEhgTVr1vjhnp+fT15e38nrhoYGamtrJ7Qu4cvc7738fbIJt3GbWdRj69wr/P7C73k4bW1tHD9+nOPHj/u3m0tOTqagoICcnBwWLFhAZmYmcXFxJCUl8eSTT1JbWzvgieXI1xvtdo5cb6LOwXwRqCukTGonT570uw4WFhb67d4PPfSQ3w+6vLx8wvq2h12+fNlv/12wYAGhUGhCX280Ojs7qaqq8vuqD9WFdDDx8fF+P/yenp4Rnzh2ztHc3ExNTQ2HDh3inXfe4Sc/+Qnvv/8+ra2tmBnTp0/n0UcfHTC8Kyoq/IAvKioacf0j13POcfHixVE9RxAo3GVSa2lp8QMrNTWVxYsX+yMcmhl37tzhxIkTE16Puro6/6rEWbNm9Rs9cLIIdyGF0Q+bHL6TFfRdiRm+knMs2tvbOXz4MPv376e3t9fvVjrQRUzhG2aEB2Yb6U1bwl0pw/vGRJ5kn+wU7jKpOef8Lo5xcXF86Utfori42A+GS5cuRT0s8Fh0dXVRXl7uXyAz0puCZGZmsmXLFrZu3UpSUtKE1bOystLvyTN//vwRfQiZGcuXL/d7q5SXlw84PEBCQgKPPfYYmzdvHvQq04GcPn3aP9k5ffr0AW9iHh6CGPoGJxvp0XvkdQ81NTUTvm90dHT43zRGe/ewiaJwl0nv8uXLfs+P/Px8NmzYAPS1p546deqBtauWlZX5wwisXbuWkpKSqAI+MzOTHTt2sH79etatWzehV06G++A750hOTua5557zw24o4QHR1q5d6w9bMFhXyoKCAjZs2MCGDRt44oknom7bjzwPMFh7fm9vL+fPn/eHEdi6dWvU4wQVFhby5JNP+s11kQO5TZTIW/OFL5qaLIb9XzGz6Wb2qZl9ZmZnzOxlr3yBmR02swoz+xczm+aVJ3rTFd78wgl+DxJwHR0dXLp0yW9LDne7u3379gO9oXFdXR3V1dV+PbZs2UJJScmQ4RYO9vCwvd3d3VFf2ToazjlOnjzpfwjl5eWxY8eOIe9QFRcX12+kS+cc1dXVgzbJhEPZzCgqKoq6bX/58uV+PTo6Ogbt6lleXs6tW7cwM1JTU3n++ef9ESgHU1hYyPbt20lNTfWve7hw4UJU9RqLxsZGrl27BvQNqDZ37twJf81oRfORewfY5JxbAawEnjCzdcDfAD90zhUBjcCL3vIvAo1e+Q+95UTG5NixY/edND116tSE9m2/V1dXF2+//Xa/Aba2bNnCjh07/GFzwz+pqals2LCBnTt3+sEeHgSsqqpqQutZUVHBRx99RHd3tx/wO3fuZMOGDaSmpvarZ0FBATt27OgX7LW1tezdu3fQMdErKyv9ppP4+HieffZZNmzYwKxZs/o9dygUYtq0aeTn5/P444/zta99zT+qPnv27KDh3tTUxJ49e7h9+zZmRlpaGi+88AJPPfUUOTk5/Z4/JyeHp556ij/6oz/yg721tZU9e/Y8kOa6yG8aZsbTTz/NihUrSExMJBQKjbrH0ngYtiuk6/uYDl+Ol+D9OGAT8O+88teAvwJ+DGzzHgO8AfxvMzOnTq0yBjdu3KCuro78/Hw/KCdykLDBNDQ08Prrr/PCCy/4Q+QuXbqUoqKifldgJiUlkZ6e7h9thoN9JIOAjZZzjsOHDwPw9a9/nfj4eGbMmMHmzZtZu3Yt7e3tQN+Rd1ZWln/DkXCw7969e8hvF11dXRw6dIi8vDzi4+PJyspi8+bNbNy48b4LvEKhkH8BWPg12tra+PTTT4fcDpcuXeLNN9/k+eefJzU1laSkJL+ffOSHQnp6OklJSf52bm1t5c0333ygvWQuXrxIR0cHSUlJZGVlsW3bNjZu3EhXVxednZ0cOXKEU6dOPbD6hEXVz93MQsBRoAj4e+Ai0OScCw98UQ2Ev4/MBaoAnHPdZtYMZAP141hvCYje3l46OztJSkqis7Nz0DbS7u5ujh496t9kob6+fsi+7eETXc65IcdXiZzf3d0d1eXuN2/eZPfu3Tz77LPMmzfPHxkxPGDXvc/f2trKgQMHhg20aLdFNMIB75zjD//wD/2bhmRkZAx4ErSnp4fq6mr27NkTVbPRhQsX+Nd//VfWr19PdnY2cXFxTJs2bcBtEK5PZ2cndXV1fPzxx1FdfXrp0iXeeustnnzySbKzs/1hDiLvUxr5/Ddv3uTdd98dUbBHnhAd7T1ewwOuffWrX/VvGhJ5ZWxGRgaXL1+e8CEr7hVVuDvneoCVZjYDeAtYOtYXNrNdwC5gRGfcJVjCR3ElJSUcPnx4yD+w8vJyzp8/T05ODh999NGQfdtPnDhBUVER7e3tQ7a99vT0cOjQITZt2sT58+ej/irf0NDAP/7jP1JcXMy6devIzs7udzKtp6eHtrY2zpw5Q2lpaVTPO5JtEY1wwF+4cME/6k1OTu7XR7+jo4OGhgYOHTo0aO+YgXR3d3P8+HHOnDnDnDlzWLJkCcXFxf2GIYC+7VBXV0dZWRnl5eXU19ePaLyYixcv8rOf/YwvfelLrFmzhvT09H5DDHd1ddHS0kJpaSmnTp0a8c2oP/vsM4qLi/27PI3WwYMH+fzzz1m3bh2FhYUkJyf7J6YvXrzof1t6kGykXxHN7L8B7cBfAnO8o/P1wF8557aa2fve44NmFg/UAjOHapbJy8tzu3btGv27mAQc8Ivcb/F50sgvHBlPhe2VfLfmDQxIiOvkP6z6PzEfFfJo7Wrernhm0PlmRlJSUlR/mOGj5GiGcU1MTKSnpyeqkRWTk5Npb28fVZNJQkICqamp94V7a2vriM8JjGRbjFRKSgopKSn3hfvt27ejDvWhTJs2bcBwb2hoGPEAYAOZPn06KSkp/nhC0HfhVmtr65iG9U1MTKS3t3dctkH4JHD4m1J3dzcNDQ0T1mvn5ZdfPuqcKxlo3rBH7mY2E+hyzjWZWRLwOH0nSfcD3wJ+BewE9nir7PWmD3rzP1Z7uwwl3A4bjZ6enqiDYiRHvmMJ066urnE7eTeSbTFSo/mwGYnOzs4JHQaio6NjQsZmH+s3pEjOOVpaWoa8T+6DEk2zTC7wmtfuHge87px7x8zOAr8ys/8BHAd+6i3/U+AfzKwCuAl8ewLqLSIiQ4imt8xJYNUA5ZeALw9Q3gHsGJfaiYjIqOgKVRGRAFK4i4gEkMJdRCSAFO4iIgGkcBcRCSCFu4hIACncRUQCSOEuIhJACncRkQBSuIuIBJDCXUQkgBTuIiIBpHAXEQkghbuISABFdZs9ic7itktkdTXFtA45XXfvf9nr4jhd/wjJCRN3g4ZoVDbH9u5UIlORwn2cGLC++Visq9FPj4vn4yubYl0NEYkBNcuIiASQwl1EJIAU7iIiAaRwFxEJIIW7iEgAKdxFRAJI4S4iEkAKdxGRAIo63M0sZGbHzewdb3qBmR02swoz+xczm+aVJ3rTFd78wgmqu4iIDGIkR+7fB85FTP8N8EPnXBHQCLzolb8INHrlP/SWExGRByiqcDezecDTwE+8aQM2AW94i7wGPOc93uZN483f7C0vIiIPSLRH7v8L+Aug15vOBpqcc93edDUw13s8F6gC8OY3e8uLiMgDMmy4m9k3gOvOuaPj+cJmtsvMSs2stK2tbTyfWkRkyotmVMivAM+a2VPAdCAd+DtghpnFe0fn84Cr3vJXgXyg2szigQyg4d4ndc69ArwCkJeX58b6RkRE5K5hj9ydcz9wzs1zzhUC3wY+ds79MbAf+Ja32E5gj/d4rzeNN/9j55zCW0TkARpLP/e/BP7MzCroa1P/qVf+UyDbK/8z4KWxVVFEREZqRDfrcM79Dvid9/gS8OUBlukAdoxD3UREZJR0haqISAAp3EVEAkjhLiISQAp3EZEAUriLiASQwl1EJIAU7iIiAaRwFxEJIIW7iEgAKdxFRAJI4S4iEkAKdxGRAFK4i4gEkMJdRCSAFO4iIgGkcBcRCSCFu4hIACncRUQCSOEuIhJACncRkQBSuIuIBJDCXUQkgBTuIiIBpHAXEQkghbuISABFFe5m9rmZnTKzE2ZW6pVlmdmHZlbu/c70ys3MfmRmFWZ20sxWT+QbEBGR+43kyP0x59xK51yJN/0SsM85Vwzs86YBngSKvZ9dwI/Hq7IiIhKdsTTLbANe8x6/BjwXUf4L1+cQMMPMcsfwOiIiMkLRhrsDPjCzo2a2yyub7Zyr8R7XArO9x3OBqoh1q72yfsxsl5mVmllpW1vbKKouIiKDiY9yuQ3OuatmNgv40MzOR850zjkzcyN5YefcK8ArAHl5eSNaV0REhhbVkbtz7qr3+zrwFvBloC7c3OL9vu4tfhXIj1h9nlcmIiIPyLDhbmYpZpYWfgxsAU4De4Gd3mI7gT3e473Ad71eM+uA5ojmGxEReQCiaZaZDbxlZuHl/8k5956ZHQFeN7MXgSvAC97yvwWeAiqANuBPxr3WIiIypGHD3Tl3CVgxQHkDsHmAcgd8b1xqJyIio6IrVEVEAkjhLiISQAp3EZEAUriLiASQwl1EJIAU7iIiAaRwFxEJIIW7iEgAKdxFRAJI4S4iEkAKdxGRAFK4i4gEkMJdRCSAFO4iIgGkcBcRCSCFu4hIACncRUQCSOEuIhJACncRkQBSuIuIBJDCXUQkgBTuIiIBpHAXEQkghbuISAAp3EVEAkjhLiISQAp3EZEAUriLiASQOediXQfMrAUoi3U9JokcoD7WlZgktC3u0ra4S9virgLn3MyBZsQ/6JoMosw5VxLrSkwGZlaqbdFH2+IubYu7tC2io2YZEZEAUriLiATQZAn3V2JdgUlE2+IubYu7tC3u0raIwqQ4oSoiIuNrshy5i4jIOIp5uJvZE2ZWZmYVZvZSrOsz0cws38z2m9lZMztjZt/3yrPM7EMzK/d+Z3rlZmY/8rbPSTNbHdt3ML7MLGRmx83sHW96gZkd9t7vv5jZNK880Zuu8OYXxrTi48zMZpjZG2Z23szOmdn6KbxP/Gfvb+O0mf2zmU2fqvvFWMQ03M0sBPw98CTwMPAdM3s4lnV6ALqBP3fOPQysA77nveeXgH3OuWJgnzcNfdum2PvZBfz4wVd5Qn0fOBcx/TfAD51zRUAj8KJX/iLQ6JX/0FsuSP4OeM85txRYQd82mXL7hJnNBf4TUOKcewQIAd9m6u4Xo+eci9kPsB54P2L6B8APYlmnGGyDPcDj9F3EleuV5dLX9x/g/wLfiVjeX+6L/gPMoy+0NgHvAEbfxSnx9+4fwPvAeu9xvLecxfo9jNN2yAAu3/t+pug+MReoArK8/+d3gK1Tcb8Y60+sm2XC/5Fh1V7ZlOB9hVwFHAZmO+dqvFm1wGzvcZC30f8C/gLo9aazgSbnXLc3Hfle/e3gzW/2lg+CBcAN4OdeE9VPzCyFKbhPOOeuAv8TqARq6Pt/PsrU3C/GJNbhPmWZWSrwa+BPnXO3Iue5vsOQQHdjMrNvANedc0djXZdJIB5YDfzYObcKaOVuEwwwNfYJAO+8wjb6PvDygBTgiZhW6gsq1uF+FciPmJ7nlQWamSXQF+y/dM696RXXmVmuNz8XuO6VB3UbfQV41sw+B35FX9PM3wEzzCw8LEbke/W3gzc/A2h4kBWeQNVAtXPusDf9Bn1hP9X2CYCvA5edczecc13Am/TtK1NxvxiTWIf7EaDYOxM+jb4TJ3tjXKcJZWYG/BQ455z724hZe4Gd3uOd9LXFh8u/6/WQWAc0R3xV/8Jyzv3AOTfPOVdI3//7x865Pwb2A9/yFrt3O4S3z7e85QNxJOucqwWqzGyJV7QZOMsU2yc8lcA6M0v2/lbC22LK7RdjFutGf+Ap4AJwEfivsa7PA3i/G+j7en0SOOH9PEVfO+E+oBz4CMjyljf6ehRdBE7R14sg5u9jnLfJ14B3vMcLgU+BCmA3kOiVT/emK7z5C2Nd73HeBiuBUm+/+A2QOVX3CeBl4DxwGvgHIHGq7hdj+dEVqiIiARTrZhkREZkACncRkQBSuIuIBJDCXUQkgBTuIiIBpHAXEQkghbuISAAp3EVEAuj/AxEitWxFNaWIAAAAAElFTkSuQmCC\n",
84 | "text/plain": [
85 | ""
86 | ]
87 | },
88 | "metadata": {
89 | "needs_background": "light"
90 | },
91 | "output_type": "display_data"
92 | }
93 | ],
94 | "source": [
95 | "cv2.putText(logo, \"Microsoft\", (370, 300), cv2.FONT_HERSHEY_SIMPLEX, 4, (255, 255, 255), 8)\n",
96 | "plt.imshow(logo)"
97 | ]
98 | },
99 | {
100 | "cell_type": "code",
101 | "execution_count": null,
102 | "id": "993a7764-32c0-47cb-9635-92df2407a72a",
103 | "metadata": {},
104 | "outputs": [],
105 | "source": []
106 | }
107 | ],
108 | "metadata": {
109 | "kernelspec": {
110 | "display_name": "Python 3 (ipykernel)",
111 | "language": "python",
112 | "name": "python3"
113 | },
114 | "language_info": {
115 | "codemirror_mode": {
116 | "name": "ipython",
117 | "version": 3
118 | },
119 | "file_extension": ".py",
120 | "mimetype": "text/x-python",
121 | "name": "python",
122 | "nbconvert_exporter": "python",
123 | "pygments_lexer": "ipython3",
124 | "version": "3.7.9"
125 | }
126 | },
127 | "nbformat": 4,
128 | "nbformat_minor": 5
129 | }
130 |
--------------------------------------------------------------------------------
/lesson7/11.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 108,
6 | "id": "1b6a569d-b1d1-4d09-9503-e3087bfea4fa",
7 | "metadata": {},
8 | "outputs": [],
9 | "source": [
10 | "import cv2\n",
11 | "import matplotlib.pyplot as plt"
12 | ]
13 | },
14 | {
15 | "cell_type": "code",
16 | "execution_count": 109,
17 | "id": "65b88433-c1a1-422c-a0ae-d81d83ca5233",
18 | "metadata": {},
19 | "outputs": [],
20 | "source": [
21 | "# img_original = cv2.imread(\"0.jpg\")\n",
22 | "img_original = cv2.imread(\"0.jpg\", cv2.IMREAD_GRAYSCALE)\n",
23 | "_, img = cv2.threshold(img_original, 80 ,255, cv2.THRESH_BINARY)"
24 | ]
25 | },
26 | {
27 | "cell_type": "code",
28 | "execution_count": 110,
29 | "id": "3b7b190d-71fc-4cdf-a9cd-0b5498a0baab",
30 | "metadata": {},
31 | "outputs": [
32 | {
33 | "data": {
34 | "text/plain": [
35 | ""
36 | ]
37 | },
38 | "execution_count": 110,
39 | "metadata": {},
40 | "output_type": "execute_result"
41 | },
42 | {
43 | "data": {
44 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAUUAAAD8CAYAAADgxrZUAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/MnkTPAAAACXBIWXMAAAsTAAALEwEAmpwYAAASFklEQVR4nO3de4zdZZ3H8fe3086UUqCUNk1t6bbGCkVjuIyFRmOw6EZZA9RUqUFBAqkLLCli1LokazZujK4R1MRUiMDiBqgCLmADdqGFeEkE24Uilxam3QJFeqHSKksKrXz3j/O0PpRepu2cOWeY9yuZzPN7fs+c8znk9NPfZQ6NzESS1DCk1QEkqZ1YipJUsRQlqWIpSlLFUpSkiqUoSZWmlGJEfCwiVkVET0TMb8ZzSFIzRF//nmJEdABPAx8F1gG/Bz6TmU/26RNJUhM040hxOtCTmWsy83VgIXB2E55Hkvrc0CY85gTg+Wp7HXDqvn5gzJgxOXny5CZEkaS3Wr58+UuZOXZP+5pRir0SEXOBuQCTJk1i2bJlrYoiaZCJiGf3tq8Zp88vAMdW2xPL3Jtk5nWZ2Z2Z3WPH7rGwJanfNaMUfw9MjYgpEdEJzAHubsLzSFKf6/PT58zcERH/BCwGOoAbMvOJvn4eSWqGplxTzMx7gHua8diS1Ex+okWSKpaiJFUsRUmqWIqSVLEUJaliKUpSxVKUpIqlKEkVS1GSKpaiJFUsRUmqWIqSVLEUJaliKUpSxVKUpIqlKEkVS1GSKpaiJFUsRUmqWIqSVLEUJaliKUpSxVKUpIqlKEkVS1GSKpaiJFUsRUmqWIqSVLEUJaliKUpSxVKUpIqlKEkVS1GSKpaiJFUsRUmqWIqSVLEUJamy31KMiBsiYmNEPF7NjY6I+yLimfL96DIfEfGDiOiJiMci4uRmhpekvtabI8X/AD6229x8YElmTgWWlG2AjwNTy9dcYEHfxJSk/rHfUszMXwF/2m36bOCmMr4JOKea/0k2/A4YFRHj+yirJDXdwV5THJeZL5bxemBcGU8Anq/WrStzbxERcyNiWUQs27Rp00HGkKS+dcg3WjIzgTyIn7suM7szs3vs2LGHGkOS+sTBluKGnafF5fvGMv8CcGy1bmKZk6QB4WBL8W7ggjK+ALirmj+/3IU+DdhanWZLUtsbur8FEXErcDowJiLWAV8HvgX8LCIuAp4FPl2W3wOcCfQArwIXNiGzJDXNfksxMz+zl11n7GFtApcdaihJahU/0SJJFUtRkiqWoiRVLEVJqliKklSxFCWpYilKUsVSlKSKpShJFUtRkiqWoiRVLEVJqliKklSxFCWpYilKUsVSlKSKpShJFUtRkiqWoiRVLEVJqliKklSxFCWpYilKUsVSlKSKpShJFUtRkiqWoiRVLEVJqliKklSxFCWpYilKUsVSlKTK0FYH0ODy3HPPsXnzZm655RY2bNjAyJEjufDCCznuuOM48sgjWx1PshTVP7Zv387ixYu5/PLLee6553jjjTd27bv22ms566yz+MY3vsF73/veFqaUPH1WP9i2bRuzZs1i1qxZrF279k2FCPDGG29w55138uEPf5j777+/RSmlBktRTfeLX/yCxYsXs2PHjn2ue+mll/jmN7/Jyy+/3E/JpLfabylGxLER8UBEPBkRT0TEvDI/OiLui4hnyvejy3xExA8ioiciHouIk5v9ItS+enp6mD9//n4LcacHH3yQG2+8scmppL3rzZHiDuBLmXkCcBpwWUScAMwHlmTmVGBJ2Qb4ODC1fM0FFvR5ag0Yy5cvZ82aNb1en5nce++9vPbaa01MJe3dfm+0ZOaLwItl/JeIeAqYAJwNnF6W3QQ8CHy1zP8kMxP4XUSMiojx5XE0yCxZsgSAYcOGccopp9DZ2cnWrVtZsWLFXn9m5cqVbN++na6urv6KKe1yQHefI2IycBLwEDCuKrr1wLgyngA8X/3YujJnKQ5Cc+bMYdu2bUyYMIHu7m6mT5/OEUccwYwZM1i5ciXHH38806ZNY8iQIfz6179my5YtdHR0tDq2BrFel2JEjATuAK7IzD9HxK59mZkRkQfyxBExl8bpNZMmTTqQH9UA0tHRwaJFi5g9ezZTpkxhy5YtLFiwgLVr1wKNmyvveMc7uOyyy+jq6mL79u2sXLmSzs7O1gbXoBWNs9z9LIoYBiwCFmfm1WVuFXB6Zr4YEeOBBzPzuIi4toxv3X3d3h6/u7s7ly1b1gcvR+3m9ddfZ9WqVTz77LMsXbqUW2+9lfXr179l3dFHH82cOXO4/PLLOe644xgyxF+MUPNExPLM7N7Tvt7cfQ7geuCpnYVY3A1cUMYXAHdV8+eXu9CnAVu9njh4dXZ2ctdddzF79myuueaaPRYiwMsvv8yCBQv45Cc/yZYtW/o3pFTpzenzB4DPAX+IiEfL3D8D3wJ+FhEXAc8Cny777gHOBHqAV4EL+zKwBp7p06dTX27Zm4jgvPPOY/To0f2QStqz3tx9/g2wt3f0GXtYn8Blh5hLbyMf+chH+M53vsOXv/xltm3btsc148aN4/Of/zxf+tKX+jmd9GZ+9llNN2TIEC699FJGjBjBL3/5SxYvXszOa9kjRozg/PPP55JLLmHKlCktTir18kZLs3mjZfDYvn07GzZs2LU9dOhQxo0b16vTa6mv7OtGi0eK6lfDhg1j4sSJrY4h7ZW/9yBJFUtRkiqWoiRVLEVJqliKklSxFCWpYilKUsVSlKSKpShJFUtRkiqWoiRVLEVJqliKklSxFCWpYilKUsVSlKSKpShJFUtRkiqWoiRVLEVJqvgPV2lQ27ZtG2vWrHnT3MSJEznyyCNblEitZilqUFq3bh033HADS5cu5be//e2b9p144ol88Ytf5KyzzmLkyJEtSqhW8d991qCzevVqzjnnHB5//PF9rvvsZz/LggULLMa3If/dZ6nITH74wx/utxABbr75Zjo6Orj22mvp6urqh3RqB95o0aDy9NNPc8stt/RqbWZy2223veX0Wm9vlqIGlYcffpgNGzb0ev2rr77KAw88QDtcZlL/sBQ1qNx4440H/DMLFy7ktddea0IatSOvKWpQOfXUUzn88MMZMWIEF198McOHD2f16tVcccUVbN26FYCIeNOR4Y4dO1oVVy1gKWpQmTlzJu9617vo7Oxk8uTJTJ06le7ubv74xz9y1VVXcdRRRzFmzBhWr16962fe85730NHR0cLU6k+ePmtQGTVqFKtXr6arq4sjjjiCJ598kpkzZ/Ld734XgK1bt76pEKFRpMOGDWtFXLWAR4oaVN7//vfT3d3NzTffzLnnnsuKFSt2nTbvyfjx45kxY0Y/JlSrWYoadB599FGuuOIKNm/evM91EcG8efMsxUHG02cNOtOmTWPatGlExF7XDBkyhC984QvMmzevH5OpHViKGnSGDx/OHXfcwdVXX8273/1uDjvsMCKCoUOHcthhh3H66adz5513cvXVVzN8+PBWx1U/2+9nnyNiOPAroIvG6fbtmfn1iJgCLASOAZYDn8vM1yOiC/gJcAqwGTg3M9fu6zn87LNaZdOmTbzyyivcdtttTJo0idNOO40xY8b4eee3uX199rk3pRjA4Zn5SkQMA34DzAOuBH6emQsj4kfAisxcEBGXAu/LzH+MiDnArMw8d1/PYSlK6k/7KsX9nj5nwytlc1j5SmAmcHuZvwk4p4zPLtuU/WfEvi7eSFIb6dU1xYjoiIhHgY3AfcBqYEtm7vxV/3XAhDKeADwPUPZvpXGKvftjzo2IZRGxbNOmTYf0IiSpr/SqFDPzr5l5IjARmA4cf6hPnJnXZWZ3ZnaPHTv2UB9OkvrEAd19zswtwAPADGBUROz8PceJwAtl/AJwLEDZfxSNGy6S1Pb2W4oRMTYiRpXxYcBHgadolOPssuwC4K4yvrtsU/YvTf+/S5IGiN58omU8cFNEdNAo0Z9l5qKIeBJYGBH/BjwCXF/WXw/8Z0T0AH8C5jQhtyQ1xX5LMTMfA07aw/waGtcXd5/fBnyqT9JJUj/zEy1quqeffrrVEaResxTVVOvXr2fFihWtjiH1mqWopho9ejSzZs1qdQyp1/xfh6mpOjs7Wx1BOiAeKUpSxVKUpIqlKEkVS1GSKpaiJFUsRUmqWIqSVLEUJaliKUpSxVKUpIqlKEkVS1GSKpaiJFUsRUmqWIqSVLEUJaliKUpSxVKUpIqlKEkVS1GSKpaiJFUsRUmqWIqSVLEUJaliKUpSxVKUpIqlKEkVS1GSKpaiJFUsRUmqWIqSVLEUJanS61KMiI6IeCQiFpXtKRHxUET0RMRPI6KzzHeV7Z6yf3KTsktSnzuQI8V5wFPV9reBazLzXcDLwEVl/iLg5TJ/TVknSQNCr0oxIiYC/wD8uGwHMBO4vSy5CTinjM8u25T9Z5T1ktT2enuk+D3gK8AbZfsYYEtm7ijb64AJZTwBeB6g7N9a1ktS29tvKUbEJ4CNmbm8L584IuZGxLKIWLZp06a+fGhJOmi9OVL8AHBWRKwFFtI4bf4+MCoihpY1E4EXyvgF4FiAsv8oYPPuD5qZ12Vmd2Z2jx079pBehCT1lf2WYmZ+LTMnZuZkYA6wNDPPAx4AZpdlFwB3lfHdZZuyf2lmZp+mlqQmOZTfU/wqcGVE9NC4Znh9mb8eOKbMXwnMP7SIktR/hu5/yd9k5oPAg2W8Bpi+hzXbgE/1QTZJ6nd+okWSKpaiJFUsRUmqWIqSVLEUJaliKUpSxVKUpIqlKEkVS1GSKpaiJFUsRUmqWIqSVLEUJaliKUpSxVKUpIqlKEkVS1GSKpaiJFUsRUmqWIqSVLEUJaliKUpSxVKUpIqlKEkVS1GSKpaiJFUsRUmqWIqSVLEUJaliKUpSJTKz1RmIiL8Aq1qd4yCMAV5qdYgDNBAzw8DMPRAzw8DMfaCZ/y4zx+5px9C+yXPIVmVmd6tDHKiIWDbQcg/EzDAwcw/EzDAwc/dlZk+fJaliKUpSpV1K8bpWBzhIAzH3QMwMAzP3QMwMAzN3n2VuixstktQu2uVIUZLaQstLMSI+FhGrIqInIua3Os9OEXFDRGyMiMerudERcV9EPFO+H13mIyJ+UF7DYxFxcgtzHxsRD0TEkxHxRETMa/fsETE8Ih6OiBUl87+W+SkR8VDJ9tOI6CzzXWW7p+yf3N+Zq+wdEfFIRCwaQJnXRsQfIuLRiFhW5tr2/VHlHhURt0fEyoh4KiJmNCV3ZrbsC+gAVgPvBDqBFcAJrcxUZfsQcDLweDX378D8Mp4PfLuMzwTuBQI4DXiohbnHAyeX8RHA08AJ7Zy9PPfIMh4GPFSy/AyYU+Z/BFxSxpcCPyrjOcBPW/jf+0rgFmBR2R4ImdcCY3aba9v3R5XxJuDiMu4ERjUjd0teXPUiZwCLq+2vAV9rZabd8k3erRRXAePLeDyN368EuBb4zJ7WtfoLuAv46EDJDowA/gc4lcYv4w7d/b0CLAZmlPHQsi5akHUisASYCSwqfwDbOnN5/j2VYlu/P4CjgP/d/b9ZM3K3+vR5AvB8tb2uzLWrcZn5YhmvB8aVcVu+jnKKdhKNI6+2zl5OQx8FNgL30TiD2JKZO/aQa1fmsn8rcEy/Bm74HvAV4I2yfQztnxkggf+OiOURMbfMtfX7A5gCbAJuLJcrfhwRh9OE3K0uxQErG3/9tO2t+4gYCdwBXJGZf673tWP2zPxrZp5I4+hrOnB8axPtW0R8AtiYmctbneUgfDAzTwY+DlwWER+qd7bj+4PG0fXJwILMPAn4Pxqny7v0Ve5Wl+ILwLHV9sQy1642RMR4gPJ9Y5lvq9cREcNoFOLNmfnzMj0gsmfmFuABGqeeoyJi50dR61y7Mpf9RwGb+zcpHwDOioi1wEIap9Dfp70zA5CZL5TvG4H/ovGXULu/P9YB6zLzobJ9O42S7PPcrS7F3wNTyx27ThoXoO9ucaZ9uRu4oIwvoHG9buf8+eWO12nA1uqQvl9FRADXA09l5tXVrrbNHhFjI2JUGR9G4xroUzTKcfZeMu98LbOBpeUood9k5tcyc2JmTqbxvl2amefRxpkBIuLwiDhi5xj4e+Bx2vj9AZCZ64HnI+K4MnUG8CTNyN2KC727XSg9k8Yd0tXAVa3OU+W6FXgR2E7jb6mLaFwDWgI8A9wPjC5rA/hheQ1/ALpbmPuDNE4hHgMeLV9ntnN24H3AIyXz48C/lPl3Ag8DPcBtQFeZH162e8r+d7b4vXI6f7v73NaZS74V5euJnX/m2vn9UWU/EVhW3id3Akc3I7efaJGkSqtPnyWprViKklSxFCWpYilKUsVSlKSKpShJFUtRkiqWoiRV/h82afOEQbIjqQAAAABJRU5ErkJggg==\n",
45 | "text/plain": [
46 | ""
47 | ]
48 | },
49 | "metadata": {
50 | "needs_background": "light"
51 | },
52 | "output_type": "display_data"
53 | }
54 | ],
55 | "source": [
56 | "plt.imshow(img, cmap='gray')"
57 | ]
58 | },
59 | {
60 | "cell_type": "code",
61 | "execution_count": 111,
62 | "id": "4ffeeecf-d1ee-4d2c-8414-911d7cb68f53",
63 | "metadata": {},
64 | "outputs": [
65 | {
66 | "data": {
67 | "text/plain": [
68 | ""
69 | ]
70 | },
71 | "execution_count": 111,
72 | "metadata": {},
73 | "output_type": "execute_result"
74 | },
75 | {
76 | "data": {
77 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAUUAAAD8CAYAAADgxrZUAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/MnkTPAAAACXBIWXMAAAsTAAALEwEAmpwYAAARsUlEQVR4nO3de6xV5ZnH8e8jVy8dEEVKwA7iZYghQ6vGYm2bBtupotb+YR1a2xrrhF40qXWaFmeaaSaZNLaTWGyiVaJ11Iy3oeNITRvHAaf9p0IPo/UCosdLKxRF6x0sHM955o/94rwyHDjA2Wftw/l+kjfnXe9ae+9nk83vvO9aa0NkJpKklgOaLkCSOomhKEkVQ1GSKoaiJFUMRUmqGIqSVGlLKEbE6RGxLiK6I2JRO15DktohBvs+xYgYBTwBfAJYD/wG+GxmrhnUF5KkNmjHTPFkoDszn87MbcDtwDlteB1JGnSj2/Cc04Dnqu31wAd39YCI8Gs1kobSS5k5eWc72hGKAxIRC4GFTb2+pBHtd/3taEcobgCOrLanl7F3ycwlwBJwpiipc7TjnOJvgGMj4qiIGAssAJa14XUkadAN+kwxM9+OiEuAe4FRwE8y87HBfh1JaodBvyVnr4pw+SxpaK3OzJN2tsNvtEhSxVCUpIqhKEkVQ1GSKoaiJFUMRUmqGIqSVDEUJaliKEpSxVCUpIqhKEkVQ1GSKoaiJFUMRUmqGIqSVDEUJaliKEpSxVCUpIqhKEkVQ1GSKoaiJFUMRUmqGIqSVDEUJaliKEpSxVCUpIqhKEkVQ1GSKoaiJFUMRUmqGIqSVDEUJaliKEpSxVCUpIqhKEkVQ1GSKoaiJFV2G4oR8ZOI2BQRj1ZjkyLivoh4svw8tIxHRPwoIroj4uGIOKGdxUvSYBvITPFfgNN3GFsELM/MY4HlZRvgDODY0hYCPx6cMiVpaOw2FDPzV8DLOwyfA9xU+jcBn67Gb86WB4CJETF1kGqVpLbb23OKUzJzY+k/D0wp/WnAc9Vx68vY/xMRCyOiKyK69rIGSRp0o/f1CTIzIyL34nFLgCUAe/N4SWqHvZ0pvrB9WVx+birjG4Ajq+OmlzFJGhb2NhSXAReU/gXA3dX4F8tV6LnAa9UyW5I63m6XzxFxG/Ax4PCIWA98F7gCuDMiLgJ+B5xXDv85MB/oBrYAF7ahZklqm8hs/nSe5xQlDbHVmXnSznb4jRZJqhiKklQxFCWpYihKUsVQlKSKoShJFUNRkiqGoiRVDEVJqhiKklQxFCWpYihKUsVQlKSKoShJFUNRkiqGoiRVDEVJqhiKklQxFCWpYihKUsVQlKSKoShJFUNRkiqGoiRVDEVJqhiKklQxFCWpYihKUsVQlKSKoShJFUNRkiqGoiRVRjddgEaW973vfUyaNInzzz+fKVOm8MYbb3DjjTfyxBNP8PrrrzddngSZ2XgD0rZ/tzFjxuSZZ56ZTz/9dPb29matt7c377rrrpw9e3bjddpGTOvqN4+aDkRDcf9v48ePz5/97GfZ09OTu/Liiy/mxz/+8cbrtY2I1m8oek5RbXf22Wdz+umnM3r0rs/WHH744Vx++eUceuihQ1SZtBMDmMUdCdwPrAEeA75exicB9wFPlp+HlvEAfgR0Aw8DJzhTHLntmGOOyaeeemqXM8RaX19ffuMb32i8btt+3/Zppvg28LeZeTwwF7g4Io4HFgHLM/NYYHnZBjgDOLa0hcCPB/Aa2k+deOKJzJw5c8DHRwTz589n3LhxbaxK6t9urz5n5kZgY+m/ERFrgWnAOcDHymE3Af8NfLuM35ytKeADETExIqaW59EIc9pppwHQ09NDV1cXPT09TJgwgTlz5vT7mFmzZjF69Gi2bt06VGVK79ijW3IiYgbwAWAlMKUKuueBKaU/DXiuetj6MmYojkC33XYb48ePZ8OGDXR1dbFq1SreeOMNfv3rXzNr1izWrl3L448/Tl9fHx/5yEeYOHEivb29TZetEWzAoRgRhwA/BS7NzNcj4p19mZkRkXvywhGxkNbyWvuxvr4+zjrrLJYuXcozzzzDhAkT+MpXvsKMGTMAmDx5MsuXL+fqq69m27ZtjBkzhlmzZtHT09Ns4Rq5BnjLzBjgXuCyamwdMLX0pwLrSv864LM7O84LLSOvjR07NmfPnp1nnXVWXnnllblx48adXmB5+eWX8+qrr85Zs2blAQcc0Hjdtv2+7f19irSuJt8MLN5h/J+BRaW/CPhB6Z8J/KI8bi6wyqvPI7t95zvfyT/96U8Duvq8Zs2anDRpUuM12/b71m8oDmT5fCrwBeCRiHiojP0dcAVwZ0RcBPwOOK/s+zkwn9YtOVuACwfwGtqPrVq1avsvv13KTG699VZefvnlIahK6sdAls/tbjT/W8PWxnbAAQfkJZdckm+99Va/M8Tnn38+r7jiijzwwAMbr9c2Ito+zRSlfdLX18c111zD5s2bOeOMM/jkJz/J9gt1W7Zs4eabb+aaa67h2WefbbZQCYiBLGvaXsQeXrnW8DVmzBiOOOKId7Z7e3t54YUXBrS8lgbR6sw8aWc7nClqSPX09LBhw4amy5D65T8IIUkVQ1GSKoaiJFUMRUmqGIqSVDEUJaliKEpSxVCUpIqhKEkVQ1GSKoaiJFUMRUmqGIqSVDEUJaliKEpSxVCUpIqhKEkVQ1GSKoaiJFUMRUmq+B9XaUQbP348M2fOfNfY+vXref311xuqSE0zFDUiTZ8+nS996UvMmzePU0899V37HnroIa688kqWLVvG5s2bG6pQjcnMxhuQNttQtaOPPjofeeSR3J1bbrklDznkkMbrtbWldfWXR84UNaJEBBdffDGzZ8/e7bHnn38+vb29fPnLX2br1q1DUJ06gRdaNKIcd9xxfO5znxvQsRHBZz7zGT70oQ+1uSp1EkNRI8rJJ5/MlClTBnz8QQcdxLx584iINlalTmIoakS58MIL9/gxCxYsYNy4cW2oRp3Ic4oaUVauXMnmzZvZsmUL119/PW+99RbHHHMMixcvZsKECQBk5rtmhqNGjWqqXDXAUNSIsmLFCrq7u9m2bRvPPPMM3d3drF69mqlTp/K9732P1157jZdeeomjjz76ncc89thj9Pb2Nli1hpLLZ40or7zyCjNnzmTr1q28+eabHH/88axYsYJvfvObAEyYMOFdgQitIO3p6WmiXDWh6XsUvU/RNtQtIvLzn/98/vKXv8xXX311l/cq/uEPf8i5c+c2XrNt0Jv3KUrbzZkzh8WLF3PYYYft8rjM5KqrruKBBx4YosrUCVw+a8R5/PHHWbNmzfZVyk719fVx3XXXcdVVVw1hZeoITS+dXT7bmmhHHHFEXnrppblu3brcsmVL9vX1ZU9PT27ZsiXvv//+PPvss/PAAw9svE5b21q/y+fY1W9LgIgYD/wKGEfravXSzPxuRBwF3A4cBqwGvpCZ2yJiHHAzcCLwR+CvM/PZ3bzGrouQ2mTy5MkcfPDBnHfeefz+97/ngQce4MUXX/Qfgtj/rc7Mk3a6ZwCzuAAOKf0xwEpgLnAnsKCMXwt8tfS/Blxb+guAO5wp2my2Dmv9zhR3e06xXIR7s2yOKS2BecDSMn4T8OnSP6dsU/afFn5HStIwMaALLRExKiIeAjYB9wFPAa9m5tvlkPXAtNKfBjwHUPa/RmuJveNzLoyIrojo2qd3IEmDaEChmJm9mfl+YDpwMjBrX184M5dk5kn9ruslqQF7dEtOZr4K3A+cAkyMiO33OU4HNpT+BuBIgLJ/Aq0LLpLU8XYbihExOSImlv6BwCeAtbTC8dxy2AXA3aW/rGxT9q/I3V3ilqQOMZBvtEwFboqIUbRC9M7MvCci1gC3R8Q/AQ8CN5TjbwBuiYhu4GVaV6AlaVjY7X2KQ1KE9ylKGlr93qfo1/zUdscdd1zTJUgDZiiqrd773vcyZ86cpsuQBszls9pq7Nix9PX18fbbb+/+YGno9Lt89p8OU1tt27at6RKkPeLyWZIqhqIkVQxFSaoYipJUMRQlqWIoSlLFUJSkiqEoSRVDUZIqhqIkVQxFSaoYipJUMRQlqWIoSlLFUJSkiqEoSRVDUZIqhqIkVQxFSaoYipJUMRQlqWIoSlLFUJSkiqEoSRVDUZIqhqIkVQxFSaoYipJUMRQlqWIoSlLFUJSkiqEoSZUBh2JEjIqIByPinrJ9VESsjIjuiLgjIsaW8XFlu7vsn9Gm2iVp0O3JTPHrwNpq+/vADzPzGOAV4KIyfhHwShn/YTlOkoaFAYViREwHzgSuL9sBzAOWlkNuAj5d+ueUbcr+08rxktTxBjpTXAx8C+gr24cBr2bm22V7PTCt9KcBzwGU/a+V4yWp4+02FCPiLGBTZq4ezBeOiIUR0RURXYP5vJK0L0YP4JhTgU9FxHxgPPBnwFXAxIgYXWaD04EN5fgNwJHA+ogYDUwA/rjjk2bmEmAJQETkvr4RSRoMu50pZublmTk9M2cAC4AVmXk+cD9wbjnsAuDu0l9Wtin7V2SmoSdpWNiX+xS/DVwWEd20zhneUMZvAA4r45cBi/atREkaOtEJkziXz5KG2OrMPGlnO/xGiyRVDEVJqhiKklQxFCWpYihKUsVQlKSKoShJFUNRkiqGoiRVDEVJqhiKklQxFCWpYihKUsVQlKSKoShJFUNRkiqGoiRVDEVJqhiKklQxFCWpYihKUsVQlKSKoShJFUNRkiqGoiRVDEVJqhiKklQxFCWpYihKUsVQlKTK6KYLKN4E1jVdxF44HHip6SL20HCsGYZn3cOxZhiede9pzX/e345OCcV1mXlS00XsqYjoGm51D8eaYXjWPRxrhuFZ92DW7PJZkiqGoiRVOiUUlzRdwF4ajnUPx5pheNY9HGuG4Vn3oNUcmTlYzyVJw16nzBQlqSM0HooRcXpErIuI7ohY1HQ920XETyJiU0Q8Wo1Nioj7IuLJ8vPQMh4R8aPyHh6OiBMarPvIiLg/ItZExGMR8fVOrz0ixkfEqoj4ban5H8v4URGxstR2R0SMLePjynZ32T9jqGuuah8VEQ9GxD3DqOZnI+KRiHgoIrrKWMd+Pqq6J0bE0oh4PCLWRsQpbak7MxtrwCjgKWAmMBb4LXB8kzVVtX0UOAF4tBr7AbCo9BcB3y/9+cAvgADmAisbrHsqcELpvwd4Aji+k2svr31I6Y8BVpZa7gQWlPFrga+W/teAa0t/AXBHg3/elwG3AveU7eFQ87PA4TuMdezno6rxJuBvSn8sMLEddTfy5qo3eQpwb7V9OXB5kzXtUN+MHUJxHTC19KfSur8S4Drgszs7rukG3A18YrjUDhwE/A/wQVo3447e8bMC3AucUvqjy3HRQK3TgeXAPOCe8hewo2sur7+zUOzozwcwAXhmxz+zdtTd9PJ5GvBctb2+jHWqKZm5sfSfB6aUfke+j7JE+wCtmVdH116WoQ8Bm4D7aK0gXs3Mt3dS1zs1l/2vAYcNacEti4FvAX1l+zA6v2aABP4zIlZHxMIy1tGfD+Ao4EXgxnK64vqIOJg21N10KA5b2fr107GX7iPiEOCnwKWZ+Xq9rxNrz8zezHw/rdnXycCsZivatYg4C9iUmaubrmUvfDgzTwDOAC6OiI/WOzvx80Frdn0C8OPM/ACwmdZy+R2DVXfTobgBOLLanl7GOtULETEVoPzcVMY76n1ExBhagfivmfnvZXhY1J6ZrwL301p6ToyI7V9Fret6p+ayfwLwx6GtlFOBT0XEs8DttJbQV9HZNQOQmRvKz03AXbR+CXX652M9sD4zV5btpbRCctDrbjoUfwMcW67YjaV1AnpZwzXtyjLggtK/gNb5uu3jXyxXvOYCr1VT+iEVEQHcAKzNzCurXR1be0RMjoiJpX8grXOga2mF47n91Lz9vZwLrCizhCGTmZdn5vTMnEHrc7siM8+ng2sGiIiDI+I92/vAXwGP0sGfD4DMfB54LiL+ogydBqyhHXU3caJ3hxOl82ldIX0K+Pum66nqug3YCPTQ+i11Ea1zQMuBJ4H/AiaVYwO4uryHR4CTGqz7w7SWEA8DD5U2v5NrB/4SeLDU/CjwD2V8JrAK6Ab+DRhXxseX7e6yf2bDn5WP8X9Xnzu65lLfb0t7bPvfuU7+fFS1vx/oKp+T/wAObUfdfqNFkipNL58lqaMYipJUMRQlqWIoSlLFUJSkiqEoSRVDUZIqhqIkVf4XctY1MNr4ezcAAAAASUVORK5CYII=\n",
78 | "text/plain": [
79 | ""
80 | ]
81 | },
82 | "metadata": {
83 | "needs_background": "light"
84 | },
85 | "output_type": "display_data"
86 | }
87 | ],
88 | "source": [
89 | "img = 255 - img\n",
90 | "plt.imshow(img, cmap=\"gray\")"
91 | ]
92 | },
93 | {
94 | "cell_type": "code",
95 | "execution_count": 112,
96 | "id": "2a91e27e-b6e0-4063-958d-1886fb0edbde",
97 | "metadata": {},
98 | "outputs": [],
99 | "source": [
100 | "contours , _ =cv2.findContours(img, cv2.RETR_LIST, cv2.CHAIN_APPROX_NONE)"
101 | ]
102 | },
103 | {
104 | "cell_type": "code",
105 | "execution_count": 114,
106 | "id": "7869d33d-d164-426d-a8b4-64f1b6a9548a",
107 | "metadata": {},
108 | "outputs": [
109 | {
110 | "name": "stdout",
111 | "output_type": "stream",
112 | "text": [
113 | "2\n"
114 | ]
115 | },
116 | {
117 | "data": {
118 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAUUAAAD8CAYAAADgxrZUAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/MnkTPAAAACXBIWXMAAAsTAAALEwEAmpwYAAAyhUlEQVR4nO2de4xkd3Xnv6er+jWPnfE88IzHMztjGTYEtDazI2M0UXCwWGFj4YAcYjZKnMgrSwsRiViRmF1p2ZX2D7N/hBA2wmtlHGwrG8OaBCxehh0DEdLaYYwfYBvMgA3zfuCZ8XT3dD26f/tH3VOcOn1+91Fd1VW3+nykUt3H7/7uubfqfus8fvcWhRDgOI7jtBgbtAGO4zjDhIui4ziOwEXRcRxH4KLoOI4jcFF0HMcRuCg6juMI+iKKRPQuIvoxER0morv7sQ/HcZx+QL0ep0hEFQAvAXgngKMAvgfgAyGEF3q6I8dxnD7QD0/xOgCHQwg/CyHUATwM4NY+7MdxHKfnVPvQ5w4AR8T8UQBvTdtgy5YtYffu3X0wxXEcZylPPfXU2RDCVmtdP0QxF0R0F4C7AGDXrl04dOjQoExxHGeVQUQ/j63rR/h8DMBOMX9lsqyDEMJ9IYR9IYR9W7eagu04jrPi9EMUvwfg9US0h4gmANwO4NE+7MdxHKfn9Dx8DiE0ieiPATwGoALg/hDC873ej+M4Tj/oS04xhPBVAF/tR9+O4zj9xO9ocRzHEbgoOo7jCFwUHcdxBC6KjuM4AhdFx3EcgYui4ziOwEXRcRxH4KLoOI4jcFF0HMcRuCg6juMIXBQdx3EELoqO4zgCF0XHcRyBi6LjOI7ARdFxHEfgoug4jiNwUXQcxxG4KDqO4whcFB3HcQQuio7jOAIXRcdxHIGLouM4jsBF0XEcR+Ci6DiOI3BRdBzHEbgoOo7jCFwUHcdxBC6KjuM4AhdFx3EcgYui4ziOwEXRcRxH4KLoOI4jcFF0HMcRuCg6juMIXBQdx3EELoqO4zgCF0XHcRxBpigS0f1EdJqIfiiWbSKibxLRT5L3y5LlRER/RUSHieg5ItrbT+Mdx3F6TR5P8bMA3qWW3Q3gYAjh9QAOJvMAcBOA1yevuwB8pjdmOo7jrAyZohhC+CcAr6rFtwJ4IJl+AMBvi+UPhhZPANhIRNt7ZKvjOE7f6TaneHkI4UQyfRLA5cn0DgBHRLujybIlENFdRHSIiA6dOXOmSzMcx3F6y7ILLSGEACB0sd19IYR9IYR9W7duXa4ZjuM4PaFbUTzFYXHyfjpZfgzATtHuymSZ4zhOKehWFB8FcEcyfQeAL4nlf5BUoa8HcEGE2Y7jOENPNasBEf09gBsAbCGiowA+DuAeAJ8nojsB/BzA+5PmXwVwM4DDAOYA/FEfbHYcx+kbmaIYQvhAZNWNRtsA4EPLNcpxHGdQ+B0tjuM4AhdFx3EcgYui4ziOwEXRcRxH4KLoOI4jcFF0HMcRuCg6juMIXBQdx3EELoqO4zgCF0XHcRyBi6LTNSEEtO7sdJzRIfPeZ8eRuAg6o457ik4u0rxCF0pnlHBP0QHgwuY4zFB5in5hrjzd5gX9s3JGlaESRaccuCA6o4yHz6uQbkXNxdBZDbgojjhayIgIRGSuy7t9L8WR+5J96v6t/VnL+Li6mXYcZmhEUV4c/mVdPlmikVdoNIuLi0tEVQolvy8uLrbf5SuE0PEu9231baGFOUvoeJl8lz8OY2OtLFKlUmkvHxsb62in+3BGl6ERRad35B06043HJwVpYWEBi4uLaDabaDabCCFgYWGhLXCW+AG/EiGrb7mPmBClCZMU6pjAxn4wGo2GKbAskPJdC6gzOrgojghFBa6b0JlpNpuo1Wqo1WpYWFhAs9ns2IZflkep+7UEjkVGbyexhFKLqhbItFSCJcBa7FjkWUDHxsbar0qlgkqlYpwtp2y4KJaUIiLYi7YsMo1GAxcvXkSj0WiLRGwb9hC1CMaEh5cvLCzkClO1aFl9WdM6jWB5prH9S4+Rt5cecaVScc+x5LgoDjErVSXO275Wq2FmZgaNRqMdOse8PikWcp3O0+nQmgXKEha9LyloAMwwPZZP1MvkOi2uOvcY247TB2mi6gw/LoojQpqwLadaLPOHc3Nz7fyhzBkCS4VC5hVjgpglHrHcn5U31MuBTpGUgiZFTHuJvJ0WwDzwNuwxOuXERXFAWPmttPVZ2xfZtmjbEALm5+fbYihzdrrqLAVJe25Wv5ZHqD1IbSPbIIVL9mOF6zok19VlyzZ9XCyWlnesPVwfRVFeXBRXmCIPVcgrbssRwbyiKHOIMpdohbT8YmHjSq3uk4WGp6XXZhVGeDvp4ekQWmINp5Fhe1oV3OpXirWVv5R2uyiWFxfFklNUTLNE2RKvhYUFNBqN9rwliNKzkoIoPSsd4mrhsfqz5rPGNMYKJrJIkiaMlj267xhp2zrlwEWxz/QylI0NbenWy8yzXQgBzWazo7CiQ+M0O7RnleYB6qE0aXaneWLW8BrtibI46nlZVIkVkWLI/WalDpzhxUWxD/Sj+hvzymJ99Cr0ZlHkaZ1HLBoiykqxNTymqM2Wl2h5vSxyLIBy/7q6bBVorGIMF1N0wca9xHLjotgDelHdzVqe16sralceUdReYt4CixSSvJ5TVtU3TRCtZVoEeb0ldlI05Q+AHNqj7ZT7jeVNnXLhojgA8ub88opckW2yPBndl75jRQ9p4WXc3hqwzfMy3yhFVd4+x7CQWXeV6DZpVCoV0xZZjdZVbKtPGWLrwdt62sPncuOi2AX99gyL5Aqt+TThyyOg8mEOjUbDLLIASwdr833PTL1exyOPPIKTJ08uEcOFhYV2Oy2KY2Nj2L9/P66//npTXPgY8wiPtFd6gFIQ2S5ez7fuSZHXOUbGGueYttwZflwUI/Q6L5THOysSGuYRt5iXaOXxrKfaNJtN1Ot11Ot1VKvVjva6aixDbO7/oYcewqc//emuvKYvfvGLuPfee/GmN71pybEVEZo0UZXjF62wPYTQ9jQXFxc7vEt5O1/eFIhTDlwUFb38IncTJvdKGNPskALI6/mil0+9qdfrmJ+fXxJW6oKDvuWP3w8fPozFxUVs3LgRmzdvxi9+8Yv2k2gsezdt2oRt27bhpZdewvnz53HixAm88Y1vXDLWkMkTPqedE+lB6mNjj1EiRdTylq19OOXD71xPkBfJcvvQhQjdt16XZzpPH1nHJHN6UgDr9TpqtRrm5+cxOzuLmZkZnD9/HufOncP58+dRr9fbfbBAyryafl6i3u8b3vAG7Ny5s2M7a3p6ehrvec97sHbt2ra9+v5qwK4S5/lM9LMd5Y9C2mdnbWcVk1wER4NV7SmulFeo2+QJfWN9xvYTGwQNdIqHvMi5iNJsNtFoNNqeoXzV63WMj48v2RezsLDQziXqYSm835deeqkdhlvHwu2PHz+Ohx56CHNzcx22WmF/US/R8uzkWEU+T9pTlMci0wOVSiXzHmcXyXKSKYpEtBPAgwAuBxAA3BdC+BQRbQLwOQC7AbwC4P0hhHPU+lZ9CsDNAOYA/GEI4fv9Mb8Y/fiSFs0nxTy7mKCl9ZXVRntCLIT84iKKFMO5uTlcunQJtVoN9XodzWYTmzdv7gg1WZCs+5str+m1117LZScAHD9+PNXL1u1jyGE40i5pgx5YLpdbhRZezudPD9VhW724Um7yeIpNAP8xhPB9IloP4Cki+iaAPwRwMIRwDxHdDeBuAH8O4CYAr09ebwXwmeR95CgisnlEL48gpoVrcl4XTtgrZDHkkJkF8dKlS+0Xe4j1er0dZjOWKOaxe2pqquMJ3VYbPdRHh+PLLbCktdV3uMgfEm0fn0/5gFktjj6Iu7xkimII4QSAE8n0RSJ6EcAOALcCuCFp9gCAb6MlircCeDC0vhFPENFGItqe9LOirKRnmNZGi0Be8Stig76AQwhLhJDDZM4fSjGcn59vL6/Vau22sWcmsrcUex6iFIWpqSlcccUV2LRpExYXF3HmzBkcO3asY1gOEWHdunUYGxvDhQsXzHNm/SDosFiPPdRYxSJenhZOyyFAXHCJjYF0yk2hnCIR7QbwFgBPArhcCN1JtMJroCWYR8RmR5NlKy6Kvcb6wlsegbUsS+TScoJ5bEobUrOwsNBRTJFiODc31/YYa7VaO6RmMdUhLNupBVHfCcLLAGDDhg1485vfjPXr12Pbtm2oVqu4//778eqrr2LLli1Ys2YNpqenMTU1hfn5eczMzCz5iwM9bXmOlicZG4jNyNxk7AERljiyMLI4Si9XCreH0+UjtygS0ToAXwDwpyGE11S4EIio0E8kEd0F4C4A2LVrV5FNV4S8wmRdpN2IW9Z+LWGwCih8oeriSa1Wa3uELIa8nHOH7EXqMYf6Aa3SA9VCYgnAxYsXUavV8Pa3vx2bN2/Go48+inPnzrX737FjB2644Qbs2bMHR48exT333NMWRTkcJ++50ueGkQKY5knK+6T1/nme+7LOgVNucokiEY2jJYh/F0L4h2TxKQ6LiWg7gNPJ8mMAdorNr0yWdRBCuA/AfQCwb9++gccc3QpYzMOLTXez/zRBZPHii5M9PZk35OIJi6EspNTr9Y6/F5Dv2gYWC2ugtkSHsFu2bMG2bdvw3HPP4eDBgzh+/Hjb/hMnTuDUqVP40Y9+hOuuuw5XX311ux/rnmML/WOkt8kjhhKrrfaY5Y9Qs9ls5xd5nXuH5SVP9ZkAHADwYgjhL8SqRwHcAeCe5P1LYvkfE9HDaBVYLgwin9hPsgQvrZDQbe5Q5gzlBcoXJgsbC6IMkWdmZtrzHD7L9rJgoqvKXEiQNmhRtEJHycWLF/G1r30Nr776akehhVlcXMTZs2fx9a9/HVu3bkWtVmufryxxySs+aWIoRVMeg/YA5XmX50qu03045SOPp7gfwO8D+AERPZMs+09oieHniehOAD8H8P5k3VfRGo5zGK0hOX/US4NHgVhlMm2ZvvvEGmfI4S+HynNzc5ibm8Ps7Gx7GXuQ2iPUoigvbF1ZlflEmTeLiVi1WsXs7Gz7bhZ9/DxfrVaxf/9+PPbYY7h48WLmcJc8OUV57iQ65NdDeOS55oKKFkQ5bMfKpTrlJE/1+bsAYp/yjUb7AOBDy7RrRVlueMvrs4Zh5M01ygtMXtAyVNZiyMNoOFcoQ2UZLvO22suRx6AHRuuKLOcT5Torp8pcffXV2LNnD77whS+gVqt1eGDcdv369Xj3u9+Nm266CQcPHmz3rcVWCnBMuLPQVWa5XJ8T+XnI8yRfHD5PTEzktsEZXlb1HS15KJJrzCN6aYUUna+Sy3UOS+cN5ThD/dJjDvkilv2zSFjjDqWA6DtYeL08Nr38mWeewcsvv9wO1YGlRaL5+Xl85zvfwXe/+11cuHChvb3uy1qWhXX3i/T29DHyPHuOlsfKP07y6TnyPHaTo3aGAxfFHtDtBRAr0KTdiSKryjzEhsVvdna2wzNk79D6n2Y55s4SHmmTDDWtu1h0Pzy/d+9efOMb38Ds7CxmZ2dTz0W9Xsfx48fb81dccQV27dq1xFPsNjS1Hu5g5Rl1UUb+TYH+IQE6h0DJUNspLyMrinm/mL3+Aqd5gnraetd3cejcIYuczBuyGMrQWY431MUTOVBZ2iQrztZxsJepParYsb7vfe/Dpk2bcObMmSU5Ucsbla9rr70WV111VWquUqPFW955E/v3vdixcn+6ks59S49Qe4aeUyw3IymKvRK6Xvdj5al42vIOdbjMYXCtVsPs7Gz7qTZcUGEPUd69YhUH9J80sR3ygauMJZwyn8jvVs5vbGwMN954Y8c+rLSA7MPqM0bWUJu08YO6aCO30WibLCG05p1yMnKiOOyCGPMOeVoKonVHihxvKF88EJsLGfKhBXIfeeyUAhZCaA/J4X5jx6KXSS8r5p1a4qRzk5JY1bgIeXK/advxvjnvKD8zp/yUXhSH7Rc5rQJtXYxp+UO+00Q+tEF7hiyIOneow2Vto2Vn7KKW4/Zig7bThEz2G/vPlViRJtaX/nsA6RXqin3eu0308XOOUNrHtqUJuofP5abUotgPQVxOn3nzhtpzk9VM9hBluCyH2HDRgoVR3q8s71XWd6QwUgx1SKvt0eIiHzsmxULeFpcH2c4SspiHaIm2FEkdSseqy1YuMfaDINMOcjud/tDbuDCWl1KL4jDRjSBmFVTq9XpHZZmfii2fbMPtpSBq9F0ZANqhtYUcniPFQg7atoawWOfEGmCt849sY1b4KcXO8gBlYUXvM2ZjFrJgk9bXsEUsTve4KC4D60KICWHMK+NlLG7ywQy6wjwzM9OuNMuxhyxWsWqqDl+1B6jttMRVeooydLTOgbVc5xLzFFFkX5YIxkLm2LhE2baIQEphtIotscKLe4vlpLSiOMhfZitcSlvOWHeQyPGH8v9SpCDOzMxgZmbGrDCzoEr08BG5XF6o1t0bPG/ZrgUUsD1GyzvU85aAy4KMPodymX7cl0YPx5HbWGMei3yX0j5r9xZHg9KK4qCwwmQ5bVVxYznEtCE30kPURRX5AFgrDI6FoZbgSA/WEkzZ1hpfaBUc0rxEDVdwmbSiiBTgtHDb6iOtONItLoKjiYtiAfJ6CbGQWXuIi4tLH/Ul/ytFFlU4ZE67O8WyVQuAlW+TxRKrgCBFXO6z22cIamGS3lye6n0asX/6s8SwiKjJ4439sDijgT8ZMyeWIFoXRFrILIsXMo8ob9vTT7jhgop8uo0U1TTSPKI0z1aiixu6XWyQtZVnk6Kqw2ZLEJcz7s+6rS/Ne4+RlQ+W7eS7U16G0lMctiR11hc+zbOSbeRdKvrBDlIM9f+msIfIomL9paimyPlLK8zo45EFC51b1H1pwbRyhWl2WLfmyaJLXk9Vj2mUFP1hybpLRn4evQ7XnZXBPcUMskJm6wUsfQqMlUeMeYlSEDlc5nuOWVjTcnhFji0WyupjsSrW+vxoQcyzb8v22O1+Mp+YhzTxyrLNmo+9W9u5x1heXBRTyBMya1FIyy/GCivyz+dZHKWHKO9h1k93iYWvVlHEOpa0kFWH+2l9Zh277pttt6ZjApv3wRCSbvKe2iuVy9lDTRM9F8RyM5Th87Ch81FA/IsfqzLrO0Lk8BvpKeo/k5K37eXJbUnbrEHSsSqszrfpd7nvarXa0Zcc6mLdOaLPpfUe8xj1Oi2WVniaFtJn5QXzDCcC7P+P8TB5NHBPURC7+GKeYsxDstbp8Yj6IbHsNco7VORgaRbVrKqvJW6x5Vo09HLplWqvMbYf3i4mEHm9qNj2acu1IOsfpViVPu1Y5HzWcCFnNFi1opgVBlvL9fZy2hrcLMXMEkQ9HEeLor6Y5YMZYrbwvJXs12MCLY8xdq7kMKC0fGBaH2x7mlcop/PYpY/T2l8esoRch9KxPuS+nXIylKLY71/dNIErsjzry689ROuvBOTfjFpiqEVI5xQBmAKosTylWO5OrreG0WgPjLeNeZ7aJtmnFkMrvJYv3U5jrdPnK8s7LEo3uU5neCltTjFtkG+MIsnxPPlDXqcHZ/NFL3OJ1v3NLIRSDGXYrB/ykJUPs8JYKzS28nK8zHr4gf7HP8sr0yJn3aWSFfbrHGfWYGuZ0+Sn9liw3VZu2OpbtrWIFYgsu10sy0dpRbFX5PH25HQszJbL+ELVuUEZQsuXbhPL21m3tnGRI4+Ia2/OKpCkecdyG/ljYD06THuGlUqlo32WrbwuTXR42hJE65xYPwxSMLmdVURJwz3F0aLUoljEW8zrJeYJpeW09VAFmYPTA7UtAbQEkfux9pW1bz4vcuiIle/Kul1Nh+V8XABQqVSWDOLWHpb1YAqZ18wSH108kTZZAqy9Yj2cJoSAc+fOoV6vdxyP/IsFHnJTqVRQqVTaNmzYsAHT09OZPzhZXqsz/JRaFPNSNGeo11u5Jytslsv1SwogP91Gt9UhtxWqxuy0/l9Fb68FRQ8Ct/qVxy7vqJEPmpX9WAJtrbMExPIMua0VXgNo26G3s1INL7zwAj760Y/i1VdfXXKc1j4lv/Vbv4WPf/zjWLduXXu95WW7x1h+hlIU8365ioS+seVZXmKaMMo2Mry0coP6D+ilUMpt8hyXZY8uiKSNF0zzHiU6LGRBlAKsQ2jeTgtqniE6WTlEyz4piGntiQif/exncfTo0dQ+Y3zlK1/Be9/7Xuzfv39J4Se2P6ecDGX1eaVIE8Q0gQTioWvMS7S8QhYZ7XVqD8/yFvUyKUhWjlD3FesvrUKt0wHyT6z0AHPLe7L6t/aVR3T0uU8bh6iPY+fOnXjd614XHYDNy3fu3IkPf/jDWLNmTUdf0j75MFzZh1NehtJTHBZi3qEVosppXaWNhciWYGUNjI4tA37lrcUET/apn0Jt5We1UHLxiPNu7DWyCMh/DowJhsbKLxYJQ7XNWhhlyoDbnjx5cokAWz9yJ06cwJNPPrmkGi/79iLL6LHqRFGHazGPK2176wKyvMA0z9DyCGWfaaG/JV7ywra2t8JUnVPUYagVlsq/Tm00Gu2qshRkLW5aVLLCegtLeOS+0jxQ+dRtAO0nlcdCd17ebDZx6NChjiFJ0kO0vHH9+bhglo/Shs9Z4tXNNlaolSVSvE6LYVoIbImiFJSYuGnPS4uQXKfbpZ0LabO1rS6w6KFFVnHI6ld6Vdq2rLtFrGOQomT9iZXVnteNj4+bVWK9H+tfEfU5jnnZTjlZdZ4ik+dLHAtvdRvtGeplljeYdtHo/xexhIPF0PJ8mSzPMau9PCYZGi8sLLSLHM1msz08R3qL0jPj7a1zGsPyJvU5zPIS9ZAjFrjx8XFs2LABlUoF9XodFy5c6HhGpeyf0wR6PzI94IwWq1YUY6SFrbFlOl+YFh4DS6u6clqKobwoY7kyiR7IneZdSaGKhab8rj3ShYUF1Ov1jvF8umghPUI5dEfbKofbSJvywGG89T/P+nilbZdddhmuueYabN++HZdffjmef/55HDp0CCdPnmy342MaHx/H3Nzckh8f7fHKc+aUm1Uviln5vCzPq2juT4eS+sVCoy9CeeHrdZaHx+ti+TuZE5MhohZWvUwKf71eR6VSQbVaXSKM1thBLU6WbbLwotvo7WP/+xy7Y4aXs81jY2PYvn07du/ejVqthjNnzmDbtm3YuHEjms0mZmZm0Gg0cOnSJTNEZ7zyPFq4/98FsVA4Fm7HhFMKIQsKv+sXExtGYuXoOMy1bNLjDGMCxe20mFmPPJNP0pHDdfR5kJ5nLO8pi1S83hrao+2N/XGVJISA9evX45prrsGuXbvw4IMP4umnn8bi4iJOnTqFl19+GfV6HVu2bMHmzZs7vELr/LuHOFqsCk+x2y9t3lxi7GWhhU4m/2VujpdJ8WBh0bfX6YHT0vPThQIdbnI/0ju0Bpnzg2VDCO1bFgHg0qVLpoBXKpW2KMfOh+XVai9PizELn/YKLRGMheOXXXYZpqamcODAAZw7dw4nTpxon1suHr3yyiuYnp7Gpk2bOs5dbBiOC+PoMNKeYp5QJm/oY/1Zk57O8k70fvXwDukxVqvVjotPiqbuQ/ef9adOeqCzzkPqae0FslDqJ4brZ0LyuEbpJephQPqHxMrJaq9R5yb1scSOlW04e/YsHn/8cbz44os4depUR+Vc0mw2sW/fPkxOTi75zKx9OaPBSHuKeYomeX/h0+70iO1D5/4sLGHknGK1WkWz2TQvQvYIpTel84sSXdG27LTESPYpRYuFRIqcrD6Pj493VKylNxvL48q8oc5r5j1OeaukzkPy+1VXXYXp6WmcPn26/Ydgsk0IARMTE7jttttwyy234ODBg+3jS3uIhXuLo8HIiqJ1AcbadLt9GpZHYb3rkEw+pYWFMZbbk33pAcpWjk6jCyjy2GVuUHti0gPkP9WyhqtI78sKj9PEJRaeStFMKyTp8yDXz87O4pprrsGRI0fwyiuvLElPTExM4Nprr8XWrVtx6NChdqogzeY8x+CUg0xRJKIpAP8EYDJp/0gI4eNEtAfAwwA2A3gKwO+HEOpENAngQQD/BsAvAfxuCOGVXhuuPYnlkNVP3oHFckybFDk5/ITX6eKKfrGA8LYyh8YixMKph/DIXKO2X3pQclspjNIblM9w1GIp/3aV84dSjFhgdJ6TbdXTlndnpR30MehwXPYpbeIw+Nlnn8Wzzz4b/TxrtRqeeOIJPPHEE+1llUqlfSxZdkrhdspHHk+xBuAdIYQZIhoH8F0i+hqAjwD4ZAjhYSK6F8CdAD6TvJ8LIVxNRLcD+ASA3+2T/R3kEcoiIW9aW11csC5Ca16Kmyys8Ly+n1gOHNbCyMLHoqO9JynWWhitarAWP96vzvOxByjvbLHyfXz8i4uLGB8fRwihLeTSQ9Yhs+UlWu1i4bWe53Yf/OAHceTIEZw9ezbze6JtuOWWW7B3795U++S+3FMsL5miGFqf8kwyO568AoB3APh3yfIHAPxXtETx1mQaAB4B8D+JiMIKJFyWG/JafeXFEkbt6fF9wnLZ2NgYqtVq+7mAlUoF4+PjaDQaS6rKclvrkVkyn6afr8heo3XnhuUxWpVuHf6zKPK0DPGlmI6Pj3f0zedCpw3kftI8LS2K8hyleY07duzAgQMHlgiq1b8eIjU5OYlqtbrEo9bese7HKR+5copEVEErRL4awF8D+CmA8yGEZtLkKIAdyfQOAEcAIITQJKILaIXYZ1WfdwG4CwB27dpV2PAV0NgoOpclvRgZ+krPSIajnCeUgiG9Mb0v9h6l15iWD+R36UXycinMsXOo+5O5Snm83I/+Y66FhYWOP+Kanp7G4uIiJiYmMD4+3h7eI71Fnpf71eIdEx9tuxZvKU4TExNmH1rApAdveeBpniCnNlwUy0kuUQwhLAC4log2AvhHAL+23B2HEO4DcB8A7Nu3r5DC5RXE5QhnngtQh3RaOKQXxN4dI8f98bsUOCloLIjcnxz/x8LEF6EMs+XdIbH+rbF+WgTYi7VuC+RiCwDU6/WOP+mS4fWaNWs6htbo2wPlXTx5KryWV6iFyhJU3TYt5RL7kUrDEmWnXBSqPocQzhPRtwC8DcBGIqom3uKVAI4lzY4B2AngKBFVAWxAq+DSE5abM+wVOv+lhVELEQ+vYe9RioO0jUW00Wi0BVC+OO+o7xyR3h+Lpi7YyH2HENoPc5ChsgyBWQQbjQaq1WqHp8ciLPfNL/0vhfxqNBqYnJzE5ORk+yk13BfvU07z+WCK3k1ijYnU28pwX+5T53DlZ87bpgmqU17yVJ+3AmgkgjgN4J1oFU++BeA2tCrQdwD4UrLJo8n8/0vWP74S+cSVQofO+gKWuTstjPr/SGSfcppzbpawyJCVBVCLkvznPC2YvI20XwqizEtyH41GA+Pj45iamsL09DTq9Trm5+c7BolzsUV6h/w3rrVaDY1GA2vWrMGaNWva4jg+Pt4WWZlzZdt07lSeq1guT/446c8mz9dQbi/Pob7LKE8/TjnJ4yluB/BAklccA/D5EMKXiegFAA8T0X8H8DSAA0n7AwAeIqLDAF4FcHsf7B4aLEGTIhN7OIFE5q1kVZo9KRYZFiopiHKZFEZeLkUR6LynWG4vK9/Sk11cXMT8/DwqlQomJyexdu3a9t0s9Xq97RmyaPPTc8bGxtpt+HXp0iVcunQJk5OTWLNmDaamptreJxeYdC5PnkMpkFrsdBpDimDa3T3yc9HpDi2Ocl9WWJ0ndHeGnzzV5+cAvMVY/jMA1xnL5wH8Tk+sWya9Cm/0kBbZv14vvQqGl8WS79rTlGGy9e9/WhRjgihFT17M+sGwMuyWfXFlmcWvUqlgamoK9Xod69ata7fnB0PwcbCAsxjyrYAsilNTU7h06RKmp6cxPT3dFkYZmsvhSjJfyufJOo8yvJbrpWesPxf9OehcsPSGrf3GBI9tySrKOMPHSN3RUiSfmDVfZH+6yMLvcpgJv1sXlR7+IS9GzuVpgdNeoM4pyjbWH2fpl/wLVimKfFHX63VMTExgbGwMExMTmJ6eXnJPtBZWeX/0/Px8OwSfmprC5OQkpqen29MTExPtd51v1I8m0/d2yx8T+RnwtDzvWYUz7Sny/oHO/6CRqRHuV750mO3CWB5GShRXCnmhybAN6Mw5yXFs+iKSoRlvyx6SFBXL07PmZXis2+gwm9vpfWjPU97bPDc3h4mJiY6QlMXRGt4jb/+ToXWtVsPc3BzGx8fbRRd+SWGURR1+ybSC9uo4X6vHdjJSvOQ7o+8o4s/C+qzkZyk/Y56ORQQujOVg1YpiVmgt18dCZy2Mer0uvMjKqr6QZP6MhVGOcZSFDxmq65dcboknbx/zOHU4zuH27Ows1q5d29EeQDsXyH8Sz/brJ+bwfnnYTqPRwPz8fFvwWAS5ACNDaplvrFar7WmZg2XSBEkeL39Gsh/eF++P78LRIiu9Tjl6gAtGciykFbK7MA43q1YUGSuvJJdZeUNNLE8ot+V9SRHUL/77UB2eacGzRJGJrcvqRwqoFkwOo2dnZzuEgr1OFpH169ejWq1iamqqo+rMQ3SkRythL7LZbHY8zZsFkD1EXsbTOudoFTr0sXNoyx6dLGjJcJ1FkT1X3Vez2Wxvw/lWPnYOt51yUqpPr5u8Xy/IKrRYv/5aCLmiK0XXSuxzLk/nI7XYyXVWSKjFMk0UdXvtYcpcIQ/UlqG+/D+TiYkJrFu3riNs5lBaPkRCP79Q2qJFS+YQpWCzMFo/NLIf/ZlYHp9OHcgqvD4GFmU+N0TUHm7ED52Q/Wti3qJ7kcNBqURxUEjBytOW4W3k3RpafOR2sohgeXl6G0lMGNOmY/uQ+9FeIXt17EVJD1CmE4DW02Zee+21jj+5ktVlfc6s5zPKNnre+lGJiaIc5qOH/cgfIA6Jx8bGMDU1hTVr1mB8fLyjH+lJysKRrn5bKZo00XNBHA5WjShm5RCttnqbLGG08osy8S/H/1nDdnh7HTrrdmnHIb1Qy6sEbGGNeZlpuUpd9dbHIsczyuV8LuT51SG8FGHLdksUZYVaD+2RBRsdKnM7GU7L3KLlYWoBjnl+TvlYNaLYLTGBtNpY01bb2MBuSwjTQuQYlpDmmdbHKEXQ6s8SaOs86fNh5T3ThgvpHKfcl/awdZ5QC5ws1OjhP3rQtrRZk5Y6cY+v3Lgo5kAKY1p+MU0MZTv5LoVRXvRpwmgR23eWQKaJWMxTTZuX/WbZytO64BOrjuv2+k4g68WCKAVSimOaGOYRt1hxJ62dM9y4KEaIeYZFhDHNi9ADgfX2Me/MIo+3ptvm6S/WVh6XFuO0fmMhphZh7UFaaQC5X5075GVWOKxDZysPGLO1CHnOhzOclEoUi+QF826vxStv/90IoyWSMn9oeZsxkZRw0UIXbmLkDcW7Cd1j5AkxLXG05nU/WsiskNrKE2oPMa93WOQ4nfJRKlHsJUUvcEvs8lSkYx6jXGcJgGzP+8o6Fl0QSGsvq7xZba3pInSTc4uF5TFhtN65mKOLKJYY5rUrtu80+10oy8WqFcU8aM8yrzBqQUsTRD1t5fPyiFzavLVfKQQxAdLkGZJkoQXd2ndeocwjNjKU1mG0NRSnW9EqmnN0ysGqEcU0gSuyrXUhZ93tottnhfFFw/luPLi8obOcTvNW04gVI7IEIy3E1tN6Gx0+s8coQ2tuZ3mKRXOj3bRxhpNVI4oWeYQx5tXoHKCuIlt9MLKfLPGLbVu0jWybVR3W/XSTc7Xsyrusm/CabbQKLloQs0Lm5eRO855bZ3hZNaJoeXpMWoFDY4mK3ibPIO883qLVfx5xKuKBZYWj2jPLe8Hn9QhjgthNocgqmqQVU/L+mLjIrS5WjSgC2YJYdBursqw9xyyvUW6b1a7I+l6gj6+b8LlbbzFPn1ZaQnuKsVe39uf1mIvkSp3honSimCZiefNxsYuKieUA04Srm1xgTBxi/eTJecUuwm5CQstDzdpPbHs5n6evvOdPbysfHqG9wqyw2XGAEopiUaSIFhlekjeMzuov5jFa+4rN59kmrd1y8lx5h5bkWbccDy2LtFv0uvUSLfJ+b3R7F+HyMJKiaOX8ioTN3eYY07w6K/Qs+tSdblmOIGYJSS/sSytSpbWV+7dCaB1Oy3bLKabEcOEbDUZOFGW+z1oeW2aJWtYQHh1eW+sswWTyeJHLJe8jzyx6KXjyfuW87a22+seOz6015jDNO0w7tuVW2GN9umiWg6EUxTxFhqLFkTxttXeXNi9JW5fn4osJRa/EUgqj3pd+uGvR/ef1gIsWabI8Qt3W8hhj7WMhbmx9L3BBLA9DKYr9oluxzNo2lrdLy8dleQ5WyF3Efk1MlNLEKq+Q6RRClofXDZbIxfKHel1e+/uFC2K5WFWiCBTLL6blCYF8openSpxnQHbW8kHTj6pulteXlU+M9bdSDOtn5aQzNKJY9Ne6lyF01n4Ya1wiT+fZXvYTW2eRJbDW/mIpgTTb8laa81DknKSdj9j9yZYnGFuWh6wfqaJ9OOVlaESxLOTxKHlZWvus7a32ywn/rf1m2bUcdEohb97Vmu5mmTVfxHZn9bIqRdESrG68PivnmKc4UyRcjtmZB/2PgFn77MaDTSOPcBXdppfeoeNYrEpRTGM5YXdeDzCr+plmU5ELPlYASrMlbzvrByDWPuuOlth2WTnEtDaO0y1DJYpFv9DLzSvmLbCkbS8pIoDdHGs3FBXRXraVopy38JElckX6cpxuGCpRHCaKenPWNtZ2aRd0P4eF9JusfGG33mGePlwQnV4y8qKYt4hR9J5WSTf9j8KFXPShFEXC+Lxh8SicR2e4KL0oFi2QFL2Qs/q2ti1aSFku3Xi1vd7vckPvPCLoAuisBKUXxaIsp5DS73306qIfhHh0W9BxMXSGjZERxSJ5uaI5vKyLsleeYZlyit2IV5FtXAidQTEyotgNecLqlaTMQtBNKO2C6AwjIyeK3VZylyOQg8rpDQvdeIjdtHGclSD385yIqEJETxPRl5P5PUT0JBEdJqLPEdFEsnwymT+crN/dJ9vz2Dyw/eZ5lY0ixxFbX9Zjd1YPRR5y9ycAXhTznwDwyRDC1QDOAbgzWX4ngHPJ8k8m7VacPOPj0rZdCQHLK57D8ipyLDH4AcBl/4FwRpdcokhEVwJ4N4C/SeYJwDsAPJI0eQDAbyfTtybzSNbfSAP+1hfJccUu0tV+AffS612t59ApB3lzin8J4M8ArE/mNwM4H0JoJvNHAexIpncAOAIAIYQmEV1I2p/thcHdQl0Ok4n11SuGLf/Yb8FyQXSGnUxPkYhuAXA6hPBUL3dMRHcR0SEiOnTmzJledp22z1TvhkO7lRSqlfRA+5Xn7FUI7jjDQB5PcT+A9xDRzQCmAPwLAJ8CsJGIqom3eCWAY0n7YwB2AjhKRFUAGwD8UncaQrgPwH0AsG/fvoG4S/Ii7fUDaWMUfSDtShL7ocjb1nFGgUxPMYTwsRDClSGE3QBuB/B4COH3AHwLwG1JszsAfCmZfjSZR7L+8TBsMaJBLzwZ6WnGXoMmzXNLs9c9Pme1UOwv1jr5cwAfIaLDaOUMDyTLDwDYnCz/CIC7l2eis1J42Os4BQdvhxC+DeDbyfTPAFxntJkH8Ds9sG0gLDcELhsueI7TyXI8RadkuAA6TjYjd5vfSmDl4oYVF0LHKYaLYg9w4XGc0cHDZ8dxHIGLouM4jsBF0XEcR+Ci6DiOI3BRdBzHEbgoOo7jCFwUHcdxBC6KjuM4AhdFx3EcgYui4ziOwEXRcRxH4KLoOI4jcFF0HMcRuCg6juMIXBQdx3EELoqO4zgCF0XHcRyBi6LjOI7ARdFxHEfgoug4jiNwUXQcxxG4KDqO4whcFB3HcQQuio7jOAIXRcdxHIGLouM4jsBF0XEcR0AhhEHbACK6CODHg7ajC7YAODtoIwpSRpuBctpdRpuBctpd1OZ/GULYaq2o9saeZfPjEMK+QRtRFCI6VDa7y2gzUE67y2gzUE67e2mzh8+O4zgCF0XHcRzBsIjifYM2oEvKaHcZbQbKaXcZbQbKaXfPbB6KQovjOM6wMCyeouM4zlAwcFEkoncR0Y+J6DAR3T1oexgiup+IThPRD8WyTUT0TSL6SfJ+WbKciOivkmN4joj2DtDunUT0LSJ6gYieJ6I/GXbbiWiKiP6ZiJ5NbP5vyfI9RPRkYtvniGgiWT6ZzB9O1u9eaZuF7RUiepqIvlwim18hoh8Q0TNEdChZNrTfD2H3RiJ6hIh+REQvEtHb+mJ3CGFgLwAVAD8FcBWACQDPAvj1QdokbPtNAHsB/FAs+x8A7k6m7wbwiWT6ZgBfA0AArgfw5ADt3g5gbzK9HsBLAH59mG1P9r0umR4H8GRiy+cB3J4svxfAf0imPwjg3mT6dgCfG+D5/giA/w3gy8l8GWx+BcAWtWxovx/CxgcA/PtkegLAxn7YPZCDEwf5NgCPifmPAfjYIG1S9u1WovhjANuT6e1oja8EgP8F4ANWu0G/AHwJwDvLYjuANQC+D+CtaA3GrervCoDHALwtma4m7WgAtl4J4CCAdwD4cnIBDrXNyf4tURzq7weADQBe1uesH3YPOnzeAeCImD+aLBtWLg8hnEimTwK4PJkeyuNIQrS3oOV5DbXtSRj6DIDTAL6JVgRxPoTQNOxq25ysvwBg84oa3OIvAfwZgMVkfjOG32YACAC+QURPEdFdybKh/n4A2APgDIC/TdIVf0NEa9EHuwctiqUltH5+hrZ0T0TrAHwBwJ+GEF6T64bR9hDCQgjhWrS8r+sA/NpgLUqHiG4BcDqE8NSgbemC3wgh7AVwE4APEdFvypXD+P1Ay7veC+AzIYS3AJhFK1xu0yu7By2KxwDsFPNXJsuGlVNEtB0AkvfTyfKhOg4iGkdLEP8uhPAPyeJS2B5COA/gW2iFnhuJiG9FlXa1bU7WbwDwy5W1FPsBvIeIXgHwMFoh9Kcw3DYDAEIIx5L30wD+Ea0foWH/fhwFcDSE8GQy/whaItlzuwctit8D8PqkYjeBVgL60QHblMajAO5Ipu9AK1/Hy/8gqXhdD+CCcOlXFCIiAAcAvBhC+AuxamhtJ6KtRLQxmZ5GKwf6IlrieFvEZj6W2wA8nngJK0YI4WMhhCtDCLvR+t4+HkL4PQyxzQBARGuJaD1PA/i3AH6IIf5+AEAI4SSAI0T0r5JFNwJ4Af2wexCJXpUovRmtCulPAfznQdsj7Pp7ACcANND6lboTrRzQQQA/AfB/AWxK2hKAv06O4QcA9g3Q7t9AK4R4DsAzyevmYbYdwL8G8HRi8w8B/Jdk+VUA/hnAYQD/B8BksnwqmT+crL9qwN+VG/Cr6vNQ25zY92zyep6vuWH+fgjbrwVwKPmefBHAZf2w2+9ocRzHEQw6fHYcxxkqXBQdx3EELoqO4zgCF0XHcRyBi6LjOI7ARdFxHEfgoug4jiNwUXQcxxH8f1+RjfV8UF0dAAAAAElFTkSuQmCC\n",
119 | "text/plain": [
120 | ""
121 | ]
122 | },
123 | "metadata": {
124 | "needs_background": "light"
125 | },
126 | "output_type": "display_data"
127 | }
128 | ],
129 | "source": [
130 | "number_tas = 0\n",
131 | "for c in contours:\n",
132 | " if len(c) > 100:\n",
133 | " x, y, w, h = cv2.boundingRect(c)\n",
134 | " cv2.rectangle(img_original, (x, y), (x+w, y+h), (0, 255, 255), 3)\n",
135 | " number_tas += 1\n",
136 | "plt.imshow(img_original, cmap=\"gray\")\n",
137 | "print(number_tas)"
138 | ]
139 | },
140 | {
141 | "cell_type": "code",
142 | "execution_count": null,
143 | "id": "2805583d-cf36-496a-b57c-0ab297af355a",
144 | "metadata": {},
145 | "outputs": [],
146 | "source": []
147 | },
148 | {
149 | "cell_type": "code",
150 | "execution_count": null,
151 | "id": "40b40c00-1150-44bd-bb97-4e6e6b7d4dd0",
152 | "metadata": {},
153 | "outputs": [],
154 | "source": []
155 | }
156 | ],
157 | "metadata": {
158 | "kernelspec": {
159 | "display_name": "Python 3 (ipykernel)",
160 | "language": "python",
161 | "name": "python3"
162 | },
163 | "language_info": {
164 | "codemirror_mode": {
165 | "name": "ipython",
166 | "version": 3
167 | },
168 | "file_extension": ".py",
169 | "mimetype": "text/x-python",
170 | "name": "python",
171 | "nbconvert_exporter": "python",
172 | "pygments_lexer": "ipython3",
173 | "version": "3.7.9"
174 | }
175 | },
176 | "nbformat": 4,
177 | "nbformat_minor": 5
178 | }
179 |
--------------------------------------------------------------------------------
/lesson9/rubic.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 77,
6 | "id": "7dd5dc72-fc78-4b06-a6c9-eb47861c4e79",
7 | "metadata": {},
8 | "outputs": [],
9 | "source": [
10 | "import cv2\n",
11 | "import matplotlib.pyplot as plt\n"
12 | ]
13 | },
14 | {
15 | "cell_type": "code",
16 | "execution_count": 78,
17 | "id": "f75ba131-1dc3-489b-8730-dca4ad61e30f",
18 | "metadata": {},
19 | "outputs": [],
20 | "source": [
21 | "img = cv2.imread(\"im.png\")"
22 | ]
23 | },
24 | {
25 | "cell_type": "code",
26 | "execution_count": 79,
27 | "id": "6e2003c6-0716-4af7-8082-212250306600",
28 | "metadata": {},
29 | "outputs": [
30 | {
31 | "data": {
32 | "text/plain": [
33 | ""
34 | ]
35 | },
36 | "execution_count": 79,
37 | "metadata": {},
38 | "output_type": "execute_result"
39 | },
40 | {
41 | "data": {
42 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAQoAAAD8CAYAAACPd+p5AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/MnkTPAAAACXBIWXMAAAsTAAALEwEAmpwYAABqKklEQVR4nO2dd5wV9bn/39+ZOXU7S1l6ly5FlCIIqKiAIFhjojEx+ZleTDEmN+16jebmJrk3uV4TNdYYuyKKooioqPQO0ju7LGyvp87M8/vjnN09CwsLyznLLs7b18o5c2a+85w58/3MtzzP81UigoODg8Op0M61AQ4ODm0fRygcHByaxREKBweHZnGEwsHBoVkcoXBwcGgWRygcHByaJWVCoZS6Rim1Uym1Ryl1b6rO4+DgkHpUKvwolFI6sAuYDuQDa4BbRWRb0k/m4OCQclLVorgE2CMi+0QkArwAXJeiczk4OKQYI0XldgcOJ7zPB8adbOeOHTtKnz59UmSKg4PD6XDgwAFKSkpUU5+lSiiaRSl1F3AXQK9evVi7du25MsXBwQEYO3bsST9LVdejAOiZ8L5HfFs9IvKoiIwVkbGdOnVKkRkODg7JIFVCsQYYqJTqq5RyA18A3kjRuRwcHFJMSroeImIqpb4LvAvowBMi8lkqzuXg4JB6UjZGISJvA2+nqvyTnLPRe6WaHJdxcHA4Q84bz8xAIMCQIUPw+Xz4fD6uv/56QqHQuTbLweG84LwRinnz5rFz50769etHz549ef3117nvvvvOtVkODucF52x6NFWsW7eOAwcOMHTo0JPuc+jQIXbs2IHL5WpFyxwczh3BYJAxY8aQl5fXouPPO6E4GbZt88ADDyAibN++HbfbzbhxJ/UBc3A4r3jttde4++67mTlzZouO/9wIBcDAgQMREWpraxk+fDi33XbbuTbJwaFV2Ldv31kdf94Jxfjx44lEIids1zSNW265BQCv10swGGxt0xwc2i3njVC8+uqrjBkzhu3btwMwe/ZsfvWrX51jqxwczg/OG6FIT09n586djbY5fhQODsnhvBEKcITBwSFVnDd+FA4ODqnDEQoHB4dmcYTCwcGhWRyhcHBwaBZHKBwcHJrFEQoHB4dmcYTCwcGhWRyhcHBwaBZHKBwcHJrFEQoHB4dmcYTCwcGhWRyhcHBwaBZHKBwcHJrFEQoHB4dmcYTCwcGhWc6rfBQO7QMRQUSwbRtN01BKOblE2jiOUDikjONXbhMRTNPk2LFjrFq1ii1btjBmzBgmTZpEVlZWvWjU4YhH28ERCoeUUCcSlmURiUSoqqpiw4YNvPXWW3zwwQfs27ePSCSCz+dj5MiRzJs3j9mzZ9O9e3e8Xi+6riMijli0ERyhcEgKia2HuiURiouK2bN3D6tWrmLxe4vZsmULlZWVjY6rra1l+fLlrFmzhieeeILZs2czdepUhg0bRqdOnfB6vfX7OqJx7nCEwuGsqBMI27apra2lsLCQffv2sX79elauXMmmTZs4evQo0Wg0foSG0tJQWneUykLkGGIVEo2G2b59O7t37+b5559n4sSJTJkyhYsvvph+/fqRmZmJruuOWJwjHKFwaBF1A5LhcJjCwkI2b97M2rVr2bBhAzt27ODIkSONFolWmhfd6InSL0GsUcAIUB1R7EcZaxBZihXdjmnWcvjwYV566SUWL17MkCFDuPjii5kyZQpjx46lc+fOuN1uRzBaGUcoHE6butaDiFBRUcGqVav45JNPWLt2LXv27OHYsWMEg0Fs244foaO7uqIZ40FNQqyRWNEBiJ2L2B5AgRqJpl2B0m/C8KwFlmBFP8Y2iykvL2f58uWsX7+eN998k2HDhjF16hRmzJhJ//7969eOdUQj9ThC4XBSjp+1ACgsLOTFF1/knXfeYevWLVRUVBIKhRLEQaH0LAz3SDRtBpY5BSvSD7EzEPHQ4LoTr9xiYFvZYI3BVsNQ2nXorq0YntexIm9jRQ8TCoXYt28fBw8eZNmyZTz77L+4/PLLmTt3LqNHj8bn89WLhSMaqcERCod6jhcGy7IIhUIUFBRQWlpCdnYOL7/8Mn/9618pLy9P2F9HaRkY7n5orpnY5mys6CCiVgaITr0owHGvG28T8SJWHrbVBaVdiu76Pt7MBZiRf2GF92BZISorK9mwYQNbtmzhmWeeYdKkSdx+++1cddVV+P3+Rt/BEY3k4QiFQ6MuRTQapba2lqNHj7Jx40YWLVrE8uXLKS4upnv37gSDQSoqKuqP0Yw8DPdMYAa2OZ5wTV5cHKBpUTgZjcVEbD9m+ALM8I8x3Lfh8n2A2G9gmasRqwjTDFJcXMz8+fPZuHEjv/nNb5g5YwamZeF2u8nIyHC6JknkrIRCKXUAqAYswBSRsUqpDsCLQB/gAHCziJSfnZkOqSDR16GiooIDBw6wbds2Vq1axfLly9m1axeBQKB+/507d9C40aFhuPuBmoMZHoNYnVooEidDARpmpCtEbkXTr8Vwr0F5XyUafBHbit1Whw4d4pFHHuHTTz7hWFEReXl5TJs2jZEjR9KjRw/S0tIc78+zJBktimkiUpLw/l7gfRH5vVLq3vj7nyXhPA5nSWKz3LZtKisr2b9/P9u2bWPNmjWsXr2avXv3Ul5ejmVZABgujZyOnSk5eicoRWbW+0TCawkFTcAmElyDbvwETZ8A+iRExmKbgxDbn3DmJFRQZYMKYtsGutYJpbljjydiQrdq1SpWrVpV7xa+YMECRo4cyZQpU5g0aRJDhgyhQ4cOaFpsjMQRjTMjFV2P64Cp8ddPAx/iCMU5p246MxAIcOjQIVavXs3y5cvZsmULBw8epKSkpN7XQdMVHfP8VJT9FrF6Eg1nI3INCJjRG7DtXQwf/W8c2HuY2uoIVnQPsB9Nfxel9cNwjQd1DbY1Gsvs0MQ4xWlZDNhoRi26vhulLce2l2Nbn2FFDyN2g+OW4dLo1MVDeqbBsSNhqiqjHDt2jPfee4+VK1fy8ssvM3r0aK655homTJhAXl4ehmE4YnEGnK1QCLBYKSXAIyLyKNBFRArjnx8FurS08EAgwOTJkwH4yle+wve+9z1uv/12tm3bVr/PddddR1paGs8991z9tj59+vDqq6+29LTnDXXiYJomR48e5dNPP2Xp0qVs2LCB/Px8KioqCIfD9fv7/C786TMpLf41VeUaVnQQIj4qyhrKDNSOBkZzcO9IgoEgLvducnLvpKgwgG0VgVWErTahtNfRjAtx+67DNq/CjOQBzXVLBBCUFkV3HUQ3lmJbH2BFtyJyFJEqELN+b3+Gmz59+7B9y/OUlWhUVSjCYRvEIrfzNEqLaqiqqmLjxo1s27aNxYsXM2jQIGbMuIY5c66jT58+9YLhiMapOVuhmCQiBUqpzsB7SqkdiR+KiMRF5ASUUncBdwH06tWrycJt22bz5s2Ypsn06dMB2LFjB5s2bWLTpk0MHz6cUaNGkZmZyfr16zGM2Nepra3FNM36958n6sTBsixKS0tZu3Yt7777Lh9++CGHDh0iEAhgWVY8jgJ0w0W33llcNLYLr7+4jFDIDZJOJHzq81RXDQbAMkdQfPRK+gx4GNP8bwoO1WBbQcQ6gG0dRmkfoBsX4Embi23PwwwPQGwXjcUi1nrQ3WUYrpWIvIkV/ZhI4DAiYer7GGi4PT76DPRxaO8iAjUD2LlNRySLcAjCCeWVlRwiLX0LPfrMY9+uaiKRCAUFBRQWFrJixQqeeuppZs2axbx58xg+fDg+n8/plpyCs6pJIlIQ/7dIKTUfuAQ4ppTqKiKFSqmuQNFJjn0UeBRg7NixTYpJWloamzdvZujQoY22d+3alezs7BP23759O507dyYrK4sbb7yR119/PfF8FBQUAFBWVtYohqC90pSfQzgcZsuWLbz55pu8++67bNu2jdra2vp9dV3h8fpwufMYPiqLXdsf4/De0RzeC6Ah9glFNoOBbXdg/+5/A34BQLee4zhWWIimFRKNVGNG1mFG1qO7Hsbtvw7buhkzMhgRP5pWi27sR3MtxjYXEAnuQuxgfem6obCs7mRme0jLuIHCQ79n11aICY3CMpuySSF2DrU1k9m5tZihFz6MZT3M3l21KFVAMBjks88+Y/v27fzzn//k6quv5gtf+AIjRoygQ4cOeDyeWCmOYNTTYqFQSqUBmohUx19fBdwHvAHcAfw+/u+CszhHkz/Whg0bUEoxevToE/aveyocX4ls2+b222+vD1j6zne+01Kz2gR1LYfa2loqKiqwbRufz8d7773Hr3/9aw4ePFg/IKkbGukZBtWV4+jYJYu87mPZtOa3rPgomRYp6loJRw6vweUuoveAuygq2I3Ibmqqo1jRQqzoI2jGKxjuMSjVB5G9WNHNREOlgJ1gr04oeCEdOnWh8PAbVJXrVJ3x3FnMpm2bvwt8F4CBw27h4J58fGlrqK40KSws5Omnn2bBggWMHz+e6667jmnTptGnTx9cLpcjFnHOpkXRBZgfv5AG8JyIvKOUWgO8pJT6GnAQuPnszWzM008/zTe/+U2uuOIKysrKmj8A0HWdDz74AIDXX3+dYDDYzBFtjzpxCIVCFBUVsWPHDjZsWM+mTZuJRKJ069aV999/n3379gGg6xq9+2UQiVyOL20g1VW/5dgRH8eOpN7WaKQze7a9TpeuKxg55tdsXLuComO1gGCbJdjm4iaPc7n6oruupXNXD4WHv03h4b5JtWv3Zy/i9pTSOe/3BAMhdO+HmNFtlJeXs2jRIj799FNmz57Nv/3bv3HBBRfUH1f30Pq8CkeLhUJE9gEjm9heClxxNkY1x89+9jO+8IUv8Mc//pE777yzfvu///u/4/P56NKlC3fddVcqTWgVEltF0WhsJH/Lli2sXbuWTZs2sXXrVo4cKaC2NoCIYBhGfSsCwO124fPNo7LiPvIP9jwXX4FjhROoKh+PYaxsdl+lFIZrBMHAX9m9rdndW0wknMvubf8FgC9tGbAVpX6JSDlVVVUsXbqU3r17M3jwYAKBAEop+vXrx4UjLiS3Y259q7XO5s8DbXq0LxgM8pWvfAWA559/ntWrV7Nz504sy+KWW245Yf9//vOfAAwePJhZs2a1pqlJJTF0u6Kigu3bt/PBBx+wfPlydu/eTXFxMTU1NY3iKww9Ew0Diyog1nEPh6Ps2bWcHv1+SKD2zwQDvVvtO8S6Ht/i0N4aNqzbTtSsbfhQ6WjuXJTuwwoXgRWs/97h0HLSMq7Btu8mWHt1yu0M1l7GoOFL2L8rTCQS21ZUVMQjjzyC2+3GNGPXskOHDowYMYJZs2YxZcoUunfvjsvl+twk12nTQuHxeHjxxRdPuU96ejpKKX74wx/Wb6tz3W0PNJUuLhwOs3fvXt59910WL17Mjh07KC0tJRQKNWoxaMqDy+iH25iJJVcgdgZe9zKi5jOEInuwbYtwaBeH9uxBaasZOLQzu7etIXE8IUnfov7V8FG3UFiwmfLSWg7uOYIZtRu8OY00XOkjUe7ZSHQSYqfjSduEbb6AWf0JYtZg2yUEat8FWYvHl8Xw0VmsW7EKxEiSzQ22ZmQ9g1L3c2DPESLRBg9Uy4KySlBEsc1ywKK4uJi9e/fywQcf0L9/f2bOnMn111/PgAED8Hg8530KvzYtFJqm0bv36T0FO3TokGJrkktifIVt24TDYYqKivj0009ZtGgRn3zyCYWFhZim2Sj4SlM+XEZX3MZkhNmY1nhqQp0Qif2Uoeg4PMZtpPteJWq9QCT6GdFIEMhnz/Z8PN50cjtP58ihpwA/4GnpN8DlrsI0hbxu79Cl293s2lbNZ5sDiB1vEUV10NLRff3R/dNRXINZOxqrKgPsmBOWqUag++bizl2OWC9j1ryHHS4GKSMcLGX9CvB4sunc9WIO75+PbihsKw2RM3sY6EYtth0FCTFizAh2bqulujJCw9SrAZofwz0CzZgNcjkoA8USrOirWJHPMM0gpaWllJaWsn79eh599BGuuupqbrrpJkaNGkVubm6jh9T5JBhtWijONxJbD6ZpUl1dTVFREdu3b2fJkiUsW7aM3bt3N3KCUhhoWga66oxhDMfQrsayp1Eb6oVdX1lUwjkUoWhPQtHv43HdiN/zBqY1n6j1GbZdQjgU5MihN/D5uyD8nEjoevzpBjVVQzmdJ7Y/rRCRUsIhi2kzrmXD6gqOHqmlMD/+3TQXyshE6V3RvKPR3NORyFSiZXmIWXe7JZxHdKxAJlbgGjTPNIy0zyB9IVZgMXZkN2KVEw4FOLz/I9yezgwclk5x4e+oLJ9MODSUBieuE9GNIP60vQRqLIaO+jVFhe9TdCTA5nVxW5ULpXJQWjd0YyyaMRfLHE+ktgNIfBxCXYjh+Sru9KVY0dewousQuxDTDHDkSCFPPfUUr732GhdffDE33ngjkyZNonv3HqSnp2MYMdvOB8FwhKIVSAy+qqysJD8/n507d7Jy5UqWL1/Ozp07qaysrN9PoaNr2WhaNzQ1BF2fiG2PI2peQNDK4oScDo2o26YTjvYgYt6FW5+Dx/gI4S1Max2WnU8wEATuw+v7Hf0GZLB969/IyMqjrHhqk9/BMIpxez+mR69niUbfo+BQkMUL4k9jpaNcOWiuXihjOMo1EcyJWOE+mNVpYDfX1Yl9Zoc9RMJjUK7h6N5bMTI+RszF2NFNSPQwkXCAz9ZXoBvfpWt3L0fy/4bH24Vg7TXHX3Gycxcg9h76DriP3duDbF1nxrtACqVlo/ReaPpwlLoMkUuxzL5EQ/4T7RQdM5SLGb4RzZiO4d6EyGLEXo5YO7GtYqqqqnj//fdZtWoVQ4YM4fLLL+eSS8YxYsRwunfvjs/na/im7VQ0HKFIMXW+DocPH2bt2rX1MxZ1g5INuSQVupaOofdDU6OBscAILHswkXAudgtDt0VchM0ewK24jSsw9HUY+kfY8iFRczuhYC2b11fg8d6Gz98bn/8raPo0aqsnAdCl+39TeqwKpe/H5X6B3Tsi8a6FQhkZaO4+KGMscBEwGjEvwKrNRqyWxHfE81JEPZjRgSi9H5p3Bpp7M7g/BXs5VngzVrSM/INBlPZVDKMTSn2T9EwDf5pGbY1NbXUUr/dPFB8LsXFNfMBXedFc3dD00cBEYAxiD8YycxG7iZbO8XaJwo5mY0cvQ9MvRjP2o1xr0VyfIPZKrOg+ampqWLNmDRs3biQvL48xY8YwefJkLr30UgYNGkRmZma79f50hCKFiAiFhYU8+eSTvP/+++zcuZOSkhIidcPrxAYk3UYvdH0iIhdj2SOJWv2w7Vxsccf3OtubSgE6ETMPmIGuTcTQr8fr/giRt4mYawmHghQc3IfL/Vt0eRndGIRtC6HAImwJYoeFyjCge9DTe6O5J4BMwI4Ow470R8wOiOVOGCs8e5vF0rFqu4LKQ7kmorkOYqStRbnexax+FztUQXVlEaj7iEZ0QkphRgURi6MFsTKUnovuuhilJiP2RdjWIMTKQ2x3go2na2usZWRbfmxrGGiD0bRrUPpOXN6ViHyAFV1NNFrB4cOHKSgoYNmyZfTv359LLrmEKVOmcOmll5KXl3fCGiZtHUcoUoiIsHr1ap5++mn27t2bMJ0ZEwi/5zI0bQ7R6ARCkZ6IpGM3lS4uacTyO1h2DpZ9Cbo2HK97Bt1yf0Z+8WIEIRqxibIF1BYQqKzzhlQGRsYYdO+t2JFLsWp7IWZmLPelJHsWJdFeQBQSycCKDkO8fUnL647m2kGosBJEQCAUtAgd50OnNA8u3xzEugcz3B0RX5LyZcSPtXVsuwuYnbC1i1DGTbi8qxHmY4aXYpsllJeXs27dOrZu3cr8+fMZOnQos2bNYsaMGQwYMKDdZBZ3hCLFVFZWHufzEEPTXChtCFFzGuFof2xa8oQ7XRKnYG00FcGlF+NxL8e2X+ZY+WqExtO06rij0DQ0Vy/EnoQVGIId9TYM+KVEJBLOrllonmoM/w5QrxDIfxsrsJf6eVcFShmAARJB4gErYoeJht7F5c3A8H4RKzIU2/QTE2JJgt11x2uInYZE+hKJ9ETpszA8O9F8rxANPYMdLSQUClFYWFgfxfvSSy/x4IMPMmXKlLO0oXVwhCKFNBW0VYdp1VATfBi38Tbp/luImrcQNnth22k0H4592hbES7FABTG0CjyurWjaQiLmB9QE92NLLKW+UqDrHmzpQW4XP5nZHo4eqsa29xEKRhErQqTsdXTfelxZcxHrJsyaQdhmOjTbxz8zewHQoii9Ft1/FN33MRJ5DbN6HXakjLqYEJdbwzT70KWHB4/nqxzc/RN69v8qRYWfothHOGQj5hEiNQ+hjBdxeaagvDdjRsbF8mTYyWq91R0rgIFY6USDI9HdXXB5KwlH/97wDeMu+Nu2bWPFihVMmjSpXUQ5t30L2zFKqcZNS12hBrpBBCmwkFqTcHQPkejv8bhfw+eeiWldjWWNwLJzEVpSAesqm42uBdDUEXR9F5q2GuQjwtHNRK2q+v3cHp0OHd2UlU4hJ3coxwr+RPERKI7Hg4y6+E727DiM1/8x5SURrMA+rOD/oPtewUifgW1fg4RHYke7ImadT0ZLktQAmo0yqtFcBWiuzaB9jB1ZRrhoF9ixQV/Dpcjq4KKmajyd8jqTv/9ljh5qON/hvU8BwoXjbmHX1hqi4QKU2oIZPUbEfAmlLUL3XIzLuBrbmohYF2BbOXGHrpbYnmC/EpQWRGmFaMZnKPUB0dBbTR5h23ajsaq2jiMUKSZRKFS2C+N3GdhZYVgsyDIT+7MoUm0RimxHsRuX8QYu43IMrsSyx2Ga3RA0Tu8GFnQtjKEXAJ+hqU3Ap5j2JsLRYkTqokkVHTp6iUamYFmjyeuRxrEjP+dYwYk+CRvXPIHbU0nPfn+hqqIal+cDopENWIFDWIHH0DxvoHkvRXdfhVgTsMP9kWhdCP9p2KwEzRVCufNR2hbQ1oP9KWZgCxIpp671kJZp4PUOprb2Gjrmeamt/h75+zufrFA2r3oJALdnI7rxL7I6vElt1W5CwWrM4FJQy9FdA9Bc09CMiYg9BrF6Y1uJXcDTQUBZaEYZmr4NWA18jB1dg20W19vv0Q0yDDflkRBWXdfoFC3OtoYjFCkmcXRb+XRkqI01sAY12kDNM9A+9sHbgqwNITUmEXM3Sh3E0Baj65fg8lyDZU8havbAPuGpF8+EraIYehG6vgXFGmx7FZbsJGodxbYDsf0UpGd66Nq9C/t2/RrbcmGZ46muuoCNq079HSLhLLZv+jUAHu9K4DO6dPs1JccKscKF2JH5KNcnaK7hGGnTELkSOzQcO+zlRHfxeHdIt9A8JbGWg1qBmKuwIzuwo0frYz8Ml6JTnpfC/P9BbDeW1Z9Q7WXs3HT61z8SHgXhUXi8MxA5wOgJ97B7WyU1lSGsyFZQu9H0BShtKLp7KppMxTaHYFvp8UHaxOt9/HeIoBuHUNqniHyCba1DrH2IXR2/5ooMw81wj48pStHLcPOfSnEwVEt7wxGKFKNpWkO0oS1ga6AJkhNFLonCcB0124X2aRq8IlifBpHqCFFrP6Z9GE19iKEPxe+5DtOaQ9jsiYgOCIZei8fYjqYtImp+QtTci22XYEsNiV2LPgMzOLz/IULBfhw74sOyRlFa3LLvEw6NB8ZTWTEGpYoZMORm9u+uxoocxYocwzbWoIzn0X1TMNJvxgyMwQ756yud5o5gpO9HaYuxQkuwgtsQuwgxYzYrBWlZLizrp4QCM6ko00DGE6hRBGpa/jtUlF4OwME9FxIKRvCnryE9+2cUHwljm4eAw9jaCpT2LJoxHsMzFys6ASua3XhUVwmaUYPh2YTYb2BHP8WK7kOkHCTWlVBK0dmbzuVeP1dbUUZHwvQ0owS9wiO6zsGWf41zhiMUKabx9JdC2XWuwfFNaRYyyMLqG0Fd5cL4MB37nyb28iBSa2LJMSy7mKi5DrfrJdK8NyJyCbragGm/R8TchGUXYUuYumYuaOR09JGZdR0H9/6J/TsVppmLiIuqxouJt5hQYDRgc2DPDjp0fIes7Ls5sLcaM1qJmJXYkd1o7rcw/NNRaTdjW31Qxg6w38QKfIwVyQc7AFLn3anRqbuPrt2msmXtP0CyEPETTPLDt6x4LABW9CJCwZsZNPzXVFU9R+HBEGJXInYltrkLpb+F7r4It2cutnkF2J1BK0PTP0GsVzFDq2M5QiVMnZJ4dIML/BlcY7iZa0YYVF1OhmViiKAA07bRTm5am8YRihSTKBQStZBgtOHDxB6E20Z6hDG/GEbN9GB8mIk8FsVaHYQqC9uqIhRZjmI1mubCsqPUhZPHykrH7c6gZ/8M9m7fSHmJi/KSmKNVNOGUyUXDjOZRfPTLFB+9jXGX3cuR/Pkcyz9EJBLGDh0gEvoHyv0SmpGGVVkGdkPFQqXh9mbQd4iP3Zs2UJyfRnF+zOZUI+JBrK7s2PwI8DdA6DlwCEf2l4OUYVmFmMGFwLvo7h5oeh62XUokdKheHBQKl1JkuzyM9qdzk6ZzVbCGvNpKdNs+YbJbgPYzKtEYRyhSTKOsSJYN4SaSUiZ2gXWQDmHMeRG0aW70j9KRf5nYn4ShyETExLIbJ4rMzPKA+m+qKr7O3hQmfDk5GqCxatkfgT9y0djRrFu7Mf6ZIJFKrEjjpkxGlo7L/UvKiu9l54ZWNrcRGnVTpId378Hn30mnvHkc3rc9XqmjWJH9WOyvP8KlaWRqBn09Pia5PMxCGBWsJScSQou3Hs43HKFIMYZhoOvxJ+TpPlIUoAQ7JwzXhdEmeNCe9GL/KQSlJ2aTdbk0/OkbCdQcwzRbvDrCWeNL+4RoeD+FhcfnU248+Arg8WrkdtlGTXU+kVCPVrPxVGh6mI5dN3GsYCpKbef4SYk0w0Vvl4dRms6lmsZUselXXY4nnuH3fBSIOhyhSCFKKVwuV8NgptCQ/uC0Coj9Y3cOo6aBetlA4kLhUR5ACEuE0pIgkchj6EYFWR0GUFr0K1qj+Q7gch8lu8PfKCsOo+lvodQ2jhTUtZq8aKoPiuGgDES2YssuIEJpUZRI9HkMI0Bml8GUFv0qvtr5uSGvx39RWX4Ej+9RhBD2cSLR0+3lVo+PK0QYEQnTMRrGiE9zns8CUYcjFCmmQ4cO+P2x5fVE5MyEAhruQg8oj0IAXelYL1hImmBsMXD9wkV1VRDUv9ADBrq+lqzcIZQV/Vcyv0ojRo37Ift351NbXUKg9lNssaitikeV0hFNG41iGrZMwKYviIbiEIb2PiILsWQLVWUhlHoVpXQ0fR05nftRcuT/Umbz8fTouwiv/0kO7glRW72USCjAnq0nNvl0FDenZ/HT6gpyzMh52704FY5QpBiv19vgomtz5kLRBD7NS+30WiQHmAb29TZZ92cRfjZEoCYMvEVV2fu4PW8xfHQWxwp/T8HByzi7Z5/Qf/AbZHf4A9s2VrDrs72EgxEsSzCjAG401Q9dm41tz8CWAYjkAD7qxgCE7thyIZq6CUP7EOF5LHsttdVB4B0qit24PEsZONxPdfmvObxvzlnafOJ3AHC5C8jrNZuSwqPYdhFmxKY6DCiFlt2R67I7kKfpPFJZhl16DE0pRrg85EZjCYU+byIBjlCklBNTvJ/luLeq+yfhVvWDfYFN5T8q4e/Q95K+HD5wGKs2jGluZ+NqSMuYzfRrO/Dh4pXYVhaW5Wu6/OPQ9CC2beNyFdD3gqkc2lvJ/l0BYvFtCjBQ5KBp41HMQWQqUas7cLx3Y+LrdGwZjC390dRsDO1dhGex7LWY0QCwg+0bwOu9lUsuy2DT6hVEI3nYjRY9PsPLpiIIUSZPv4YdW7dSUhgif28oNgahNHzKwNO1BwePHMCoKEGvLEUBB5XG2wlfQaDdTm+eLY5QpJhGDlcCRM7+eRQTnuPiO92xv/1b9qPVaPSd2IfD5flQIFRXVvPewmrSM3szatwwVix9AU3PIRrpdELZhlGD4TpKOGQxeuLXObBjPWUlgYTVuTwoslCqH7qajqirsexRsRDuZqNfE7e7sKU7tnwFTV2PS38b234BSzYgdgnBQJDVy4K4PQMZNq4HW1cuRtMzscyup3mVLHxp+wgFbXK7PowZ+TsfvxeJB40q0jSDHpqG3rM/zx7LZ9SRAw3W1a2qlrAapkpaO6J9tkccoUgxjRKUCPG0cGfJqRolCuwMm31b9pOxPAPff/mIrIkQPBKkpirMJ+9tIDNnBGnpc6gsv5NIaBym2QFUlPSM9/H7l5PT8a8c3FPLuo/rZlgMFB1A9UFjNEpNRxhH1D6dhYdPYSgAOrZkY1u3oqkZGNpyROZjy0qEQ0TCNWxZcQiPdyj+jKnUVN2NbY3FMvNOWnJa5lIi4WP0HXQX+3YEKSmI9/cMN0Z2B2ZUlnNRega/KS+BfdtPYWHDdzrjlRZPSvv0pHCEIsXoul4vFiJAEpyfjs8dcTKqJ1ZTPb+abi92xdps0vMvPTgUOExVeYTqilfp0PFNbOuriPRBJIgv7Q+UFoUoOlpXfgaa6odiLHAJwhhsGYhIBifGcJwN8cxRkoMtM1CMQ1MbgWUIH2DLZsKhasKhpfjSP8LkSxjuYfS9II0dG78NKDJzNqAbS6ksjeJL+xOhQCnb1sdjMnzpXG9GuEA38GTl8OuSo6jyZlZhTkCAqPZ57XTEcIQixZwwRmGd/RPlTJvBR24phFsgc0wmErLRt+m4HnRRWhwC9Xc0TWHbQnFhXfnpaNrlIFcijEIYiC250KKw9zMh5pUpdMSSy1GMQ6m56GoF8C62rCBYUwY8g8ujEazx4vWtxuXRsO3tSHQdgklJIaA0tNzOTMzI5JuF+UwRmx6hAOw9eQviVFjttMuQLByhSDGNhEJowWrhyaPghliSCVWliMyNkPnHTEIvhYhYjfMiKOVHU5dhyy1xgTjdMPdkEUvZJ2QgMgYYimImuvYhIn/Fkk1EwzYH9wTQ9GcwzViuTAB0F0bP3nx8eC9GdQUdgrX0C7d0ndnEVlP77DIki893e6q1Ec6uRSGN/ml5MZmCfbFN9ePVDL9yaNx5qwFbijGtP6DU3RjaxygCxHrprRWtIMe9NtCUPy64jeeXbQvMqKB5/fgumsxbmdkUFuxnHMLYSJh+ZxNymmBL0r51O8iP2RROiyLFNJ71kCSNiiXntpV0Yf27G9H7aHA4vlHFyhcpwrSfA95EV5ej1Fex7PEIOcCJCw8lB0n410SpWnR1AKXmY9tvErV2AKETjvJmd+TenA78at3HSR05iaFAhEjd67O99u20YeIIRSvQKMty0m6UJBWkgUIDbJQH3CMUYoC1R7DKAasaS95Ayado6nJQ8xC5BJFuCC1NfXc8Den7FLUodQRNrQf1Hra1FJt86vNkalpMRuqSFSvFlGAtv6koOUsbmqAu6heh+vgU3y0pLl5ae6RNC0U0GuXJJ59stG3u3Lm88847hEINT5YJEyZw+PBh8vPz67f17t2bq69O/WrYzdF4MJOz88xUx79J1k0Xnx3oCPpvwO4PxhINe4lgrQOzUBC7BEteRslSNG0SSl2FyAREBiCkNWXgaZ8XImjqKIrPiKWSW4Zlb0SoAARNKbI9XgZ4PAw2DIJK8WFNDcWhUOycWmriWpRS9Zc5GX10JbHv0h5p00IRDof5xje+wfDhw+nTpw8LFy5k6dKlLFiwAJfLxZ133slf/vIX/vznP/POO++wePHi+mPnzJnTZoSikcNVoC0+UeI3rwsinQRzMGj9BGOmQl8FxjsKaxlECwQxS7DsBSg+QqkLY60MrsKWYXHBOJ3Gf2ysQ1GDpnYCK4BPETZgy2HquhcuXaeb3884n4/LlMZF0Qh9o1FChsHvcnN58sgRToylTT4KhdvjbX7HZtBFMByhSD5er5fFixfTqVMnsrKyCAaDvPjiiwBkZ2dz00038Ze//KXRMQsXLuTYsWPce++9PP7443zta187F6bXk+jGLQJUaS1fUiJpq3CdtOB6bDdE+gmqF+iXgbFF4X9Xw1woRA4IYpUjsgzYgOJ1NDUV1I3Y9iiEOhfxpnJN2miqFE2tQORtbFkLHIy3HmLNrXSPh1HZ2VxpGFwaDDIwEKBzJII3Go1lMNc0Ls3K4hmlMEUQOzVTSRL/nyCUB2rOfhBZtdeORxsXCsMwmD59OiLC3//+d1auXAnEnJhWrlzZqKtRx+WXX86BAwcoLi5m7969jT6ry3rcmtmPG7UoAA1PfE7+bGxI7uxDkyXVzegaYHYHs4ugjxfcNyvSX9QIzxci+QJShbARS7ajZAG6djXwJSx7LII7obgourYPxVtY8haWvS0uDhFiuTIVHXx+JmVnc73LxaVVVXQuL8dnmuj2ieHcfsvihIQRSUYprb7rETHP3lNOCWjts0HRvFAopZ4ArgWKRGR4fFsH4EWgD3AAuFlEylWsM/4XYCYQAL4iIuvPxkDLsnjllVf43ve+h9vtZuXKlcyZM4esrCy6du3Kn//859MqxzRNevTogW3bGIbB/ffffzZmnTYej4esrCw0TcMWCymKxBLsqrpckWdeZpOxHmfBKU2oO40BVjYExwtqjOD7lob7CUXkFTvWJYmGENmHaT+C4kV0bS5wM7b0RFOHgQVY8hYihcRS+MX66z5dp2daGrNyc7khGmV4aSm+UKheHJq0UQS9NUK9dR0sFRekZDjKtd/w9NMZo3kKOH5d+XuB90VkIPB+/D3ADGBg/O8uYskIW4xlWSxcuJAvfOELdOjQgZdeeolx48ZhWRZDhgxhzZo1/OhHP2p0zJYtW9i5cyeZmZnk5TXEAxiGwdGjRykqKuLhhx9utBR9KsnOzubyyy8nKysLLMFeHkFfmwa1eosbBq2+HoRK+NNAvBAYZBP4nY2+UJH2Kw3PGIWWCWg2Qhmm/QSmfSMi0zHtGzHtvyNyCKVM/IZOb7+fazt14i/duvG218sDBQWMP3yYjEAAI55vMvHvBBKvQaq82BLHE86yhsfCfFSj2XGtHbmFN9uiEJFlSqk+x22+Dpgaf/008CHws/j2ZyR2J69USmUrpbpK7DFyxgSDQebOnQvApZdeSjAY5OWXXyYSiWBZFh988MEJx4wbNw6IDWZ+//vfb8lpk4qu68yaNYs333yTd955B3tDEO1HPrQbfchUExkYhTQruaETrYEC2wXBIYL2U8E9S8OzEOwPwNosmKUANQgxhydD0+jo9THQ5eISt5tphsFFoRCdysrQTPOMv7pOvGWVUtFs+FGOz3h1JtQdesxwUWnGhl/9fj95eXntYoFiaPkYRZeEyn8UqEvU2J0G1x2A/Pi2FgmF2+3mt7/9bf37bdtimWN//OMfA7EWx29/+1smTJhAp06dmDhxYv2+gwYNaskpk45t2xw8eJBAIBDbEBXsFQH4TEdb4EZd4YUrBRkVQXzxMfz2ce/EULElPEOjbLQh4LpB4V6sof+fEN4TqyJew2B6VhZzDYOLo1H61dTgC4dRCZmqzwgRNCvedRNSJxaNnvjqjHt7dbtGNZ2Dbi9PKI2CSAiXy8XEiROZOnVqu2lVnPVgpoiIUuqMfyml1F3Euif06tWryX3cbje/+c1vTqu88ePHn6kJrUI4HOb1119nzZo1jbsMVRb2siBs0FELXKirvKhZgowOI36zVcUiKdVMge2F8BBB7yX4gzqR31hIFIZlZfETTWN8eTmuSIOP49mfM15zUyQUSjdAqXi34cwqtABBw8Vuj4+PNJ0ltsWngRpqLJMMfwaTJ0+mW7duKbE7FbRUKI7VdSmUUl2BurTLBUDPhP16xLedgIg8CjwKMHbs2PY6a9Qs4XCYo0ePEo0vrpF2QSZp30mn40/y2BXdglkdRdZbyE4NtUBHm+GDL4E1LADuBO+sE7omyZz1SOLlV2D5QMYIygMShZ4uF70DAVyRSNL0T1eJMbQpEgrD1eCdqermtE9+rnrvELebVf4M5iuNT0K1FISDVFkWZnwsJRAI8Nxzz9G/f39mz57dLrofLW33vAHcEX99B7AgYfuXVYzxQGVLxyfOF3w+H7m5uWiaho7OwPShFH/rKDuLNjHuS5fRyz8AAwNqbWR7FOuhGuybIxi/zkTfngHRuN+FrsCI3VAq2QMaKahnSqfexFTEnmq23QoVrKH8sOE6IedQ3Vi0DUSUxmFfOk93zOMWXzq31FbzWEUxW4K1lJlRTKS+K2NZFjt37mTjxo1YVhKSqLYCpzM9+jyxgcuOSql84DfA74GXlFJfAw4CN8d3f5vY1OgeYtOjX02Bze0KTdNwuVwNCxUrDXHZWNnw6T/fB+C68beyrGQJFbUlcAxkbxjzv8JoL3sxvpiJPc9EVYCEYjdVUlsAKUJS3fW27WTHdZ5IghDZunHC2aJKo8ow2Onx8p7LwxtmlG0VxYRNs/74NMOgq8tF5rBheHv2ZPMnn1BTXIxt25hma/iVJofTmfW49SQfXdHEvgJ852yNOt9IfPJZHNedABaseh4AfbOB68cezJ1h7MM29v4Q9u/DqOc90EHH3hHr30v8v7aMsmioVSl48GsiCXk+UnQtdK1eLCxAlIalhGrdoFA3+MztZaHLxdJQkMKKUqx410IzDDzZ2UypqWFydja/OHoU1q6FtWsZOX48m4uL42a37d8wkTbtmXm+UL/2KGCeIjrButDEes/E+6of86Mo3qf9BKtqkX0hZF/DfhE7ctIy2gxKpTT1QuIYRerqW8Pvti8aZaU/nWoRPlUan9oWn0WClNVUxCq8UrjS05kZidDfMMjKy+NXW7eijh5tVKInJydVxqYURyhSTuPoUfs0ElKEbgjADeAa70EVKTJ+nEOVXVb/eUSieO7xEH403HanUhPtSlFFTvVgJpYZiy0BVtdUcLfHS63AoWiAYNylWymFr2NHLs3I4NaiIqaL0DMQgK1bm7a5nUyHHo8jFClGqcaZuE05/X5p8Is1YELoolq0j3TUrxRWvEViPh5F26mRcVEGlf9dmRLbz4ZUd470VhjMtKvLY2IB1Fom6xOyZWmGQWaPHsw/eBB3TQ1dwmH619Y2W2Zb1fXmaJ/y1s5ITK57qq5HkxgQmRym0/A8+rouqN9siY39sU31w9X4evrwPuWNDb/XZaw7z2m8rF+SMn7RcAkf9Ph417ZP6Ne4vV46jxnD2+npbMvPZ4oIE0Mh+ldXn/Y56mgP06J1OELRCtR538VuxJZNhx2bU8Cen29r2JChgU9hmzbB/CChr4XI8WVzY/b16MdalshFiIVCJ4UU1wHtuKTFZ0uZprPH5SJ97GS8vjR+GQ4SMhvGglwuF3fk5lITClGwfj1XVVTQtQWu54m0l6lRcLoerUKim+4ZtyjqC6FB1g2F/kA6YpnYC0zYYkK5TXmkglcir5E9KIuKJZX4lA/VDQLdTi+Nm1Ik7dGhUtyyMTQNvdFSjWfOMbeHw5qGhELM7tqLY4WHYO3HwPHJxBTDunThqSbSGrQUEcGOR8hK4gxOG8URilYgcYwiKT13XcMaGYLxUZjlQr3jgbcsZKMFRRYVVZVol2h01HNxX++idm6AshllRHKSsPrQaSKJPmEpqAP1QWEtoFppvOFP4920DJ7TDayiAijYD4BPgx66opum2GUKRy1BlMI/aBAkUSggFgdkpyjpTrJxhCLFNE5cI0QkSVObygZDoH8E+bqGulJHfWrAYhd8ZGIXmRy28tFf1unxWne8X/ExqMcgtvxma6uMqClJ7WnchoGhx7tYp6m9f+k7iKPHjlAeCvCobiDFR0FsNCBLVwx3aUxRMF6gu6Z4UAnzbSu2uJvH00zpp0k78p1IxBGKVkDX9fqnnyXJeqqrhn88NjLIhr4KrjBQq3XUAgNZYmIVmxy0DqE/rlNqlJK1MZPuo7qz7bctWzHrTM0DUtIF8es6njqhaOYEz2Zk84pl8UFVBVXRSGwxkKpydAW9PBpTNcU0gQttoa8lpFtCxFDkGlpDTyxJFbzB9yPW9WgvTleOULQCiQ5XtiRhAOv4UI+6126B3lGkm4LJGmq1C/VPF/b7EawKiyNmIfoCnYNLDtH7lV5EfhVh4PsDWHtsPQECZ29XAslN1nciBiSMUZxIheFi8shLMLdtpDhQQ6nYEIjNTLgVDPbozDY0Zpg2F0RssmzBFTe4qVK1JLlbS70rv2q8gHUbxxGKVsAwGi6zdVb5+uOcLAdDXXCjSyDPQmZZyGQd7UMvPCbYy0NYNRa1tbUEPgugf0WnzCwnbMYW7BUBzU44R/u4h7FRBBJCzi/qM5jD+fuo3bAy1nogNqaRocFFXoMvGxqXhyw61kZxy8mHUhppcQqe/I0Wh2rjOEKRYho/OQTrDByuWnbChNc6kGNhz62Fyw20jz3IE4IsjyLlFmbIbDQLo2rAs1lDhthYLV2qo+6YFIuMLoIWr7xLfX6yBwxDqisx8/fBgR2xfYB0DbrrGle4NeYCF4UtMgONf4OmTFVCffnJRLlcze/UBnGEohUwjAa/htNx4U4aiY/KLBP7WhMmGmhL3MjrNrLShHyLOq2wyyD6J8FbqmFeI5j9pWWCIbGK1mDH2atGXXGmrlPl8bDFMKiJ5/iQYC3RLavr9/Uo6KorRuiKqbrGFSJcELLwxtd9PW1rUtF30hICzSzLmfVwaMDj8aJpKRrMPNPdO5jYN5pwmYH60AV/1ZA10Vh4pA2RHYL1O8H9rsJ9pYZME6IXCpb/DE6rOCF3Q0upq6thj4fDfj/rNY2VmsaHVVUUBxv8QxSQayiGaIqLNMVkYJwtdA6aGC2dgUk4SJLsHCUimKbZbpyuHKFoBdLT02NrRNDKLYqmUMTa5Hkmcr2FKvDCVhNqGh6fVjUEPxT0tYI+X+G+UsEsiIwUrHTOvNa1oAkvgGgaNWlpfOb386Gm8WkkwpZgkGPhMOGECuZSMN6t8yUNLjGFPtHY4OTZTtE2GqNI0pP/eHucWQ+HelwuV9sbtFKAS1BdQOI9I4/yMMh1AdV2DYfMQ1jVFtZaQdsB+pvgvkJDviRELhTsM1mf+DRra12VsQyD4owMPvX7WRCNsq6mhiPRKDWmidVEhe2gKW7V4PawjS8hXfZZiUR82ubsfD9P5PhYD2fWw6EeXdeSm2QlmYOFCWWZQ022fbAdQbjoO2M49MYhjoWLsGsE+zMw99gYC8E/W8P6f0JokMQyWR0/bZA4e9IMkvCv5fFwIDeXN9xuFlRX81lxMVWmWb9yuUJhpHXAGDMZRBFa+TaYEQwgR8Brp26BnWTNetRfKqUwDANdT80Cy8nGEYoUE7shXI0iSJNCsopJyESlu3QinWKeo6tfWAMC14y+mk+LlxM5GiESjhDdJ0T/auN5TZF+m0b0eiEySLD9NMSJqNhiaCeztV4clCKq61R4vezKzma+YbCwqor9R4/WiwOajuZLJ8+TxtzMHP56aAd8HEvR2qFDd6rKCkAluIwnrSV/3PxwCtLWOdOjDo1I9MxMClL/v7PHSiwn4XX8/n1n87v4jvm45NaxfHZ4G5G9UWqllvBhIfx7wf28wnuzhjlHsAYLVjanbO0IYOk6lW43hzweVvn9LBRhVWkppaFQvM+uwJvGCDNKdnou2WMm8MbS16DiWKOylOGqLzSZl6SuzMSGUrJaFE2V0h66H45QtAJ+v7/tPjkSs2+dpDIEuwT5eOmndPuoK1nPZ9HxrY6UFJRQIzVEDgjR/xHcbys8MzTsawRrGOiFqn7aNaoUpmEQ9HopdLnY5vPxia7zYTjM9pISquNrfaDpqKwODHN5mKA0flpVwsCKQlj62ilttxVYSiW5RXHcFG+yykx+ka2CIxQpRilFly5dSEuLOSS07aS4p7btyJRCmAJ9X+uDlq9QtQr/L33URgKEtwrabsG1SKFfDNFdNnYodtzOQIBXMzII6zprTZOtoRD5gUBDtmrdjSevL78v3IPSdEZhM6XoNCI19QbxTVoejZORghZFe2hJ1OEIRYpRStG7d2+mTp3KoUOHsA8Irv9wE/lV6CwKJSlOTECLnsD7rz8QexGFyEVR3B+50R/UCYaDhLcKagexdYPjZe+trua/IhHClkVNNFrfclHeDLTBo/jbni30qyrhcttClR1t8pxNkpC3RlRyex4K0BIvcZL8HSKlpSCCruv4fL52IxZttD18fpGRkcGXv/xlsrOzkRqb6O8jZA7ogP+t9JZFT50s1qMlNFpe8wxvWhdEr4oS/XmU0J4QObOycSkXYkKiu4hl2xQHg1RFItgCKqszc3sMYk+4lt071nNHbRVXVJeeXbYoSGq7XgF+Fb88IpAEPwoBKrZuRSlFjx49mDBhQtvtkh5H+7CynWPbNsuXL6c6nldRAjZVe8sIzQvSK3MA2mEdrebc/BSN6lYLtUfSBeknlL9WQTQQJa9XF7Tjby3dTWaHnvSfeTuByiJeLNhFP7HpG6rFLS2shKohxWCyUQJupZJSQSJAFXBVbi4Hy8vxer3cdtttTJo0qd20KNp018O27foVzOvo378/Bw8ebLTKUl5eHjU1NdTUNGRJzszMPOnix63N0aOFzJ8/n0gkEquZvth2O2hxKLoHrbdO7+4DOfjubrQOOmbXVsxElcxa5o79c2x3EYPHDGLHZztildiTxoBLpvHJmqV0efuZ5J04IRdp4npDycKOp+oXztyF2wZ2+/2YwSDP+f38kXi3A4hGo2zdupWCggL69++fZKtTQ5sWikAgwIgRI8jLy6NDhw5s27aNP/zhD/zHf/wHkUiEcePGsWzZMv785z/zzjvvsHjxYmbOnMnbb7/NnDlzWLBgwbn+CgBUVFRSUlICgEoD1/U60hnsTwR7m41dZbG/YCfeEX58M9II/b8A0UvDmJ1ONXefpCdRQjFakp5u4hZ2LNyJp5+HkIQZk9WJZ9d+RJdQcnNe1GEBQVFIkqc9Ep/20dNIxV/HRxkZFAWDfKN3b6r27sWKH6sRExDTNHnnnXe46KKL+MEPfoBhGG2+ZdGmux5ut5tf/vKX/PGPf+T2228H4J577qG6upqcnBweeOCBE4556qmnANi1axdLly5tTXNPSiN/fr+CWQrr1zb8D+j3aOjjNZQfQhKg4u0S3Dd4MH7mpuuDPWlpLt4zMK7+pUpiJ1+hMIj5OdxVdIAhwdNLZ39mJ0nMbp58XKph2MY+jRbFR14vD7hc3O718gWgfPt2rEiEdA0u8mjMS9PpFF9oOhgMcuDAAUKhcAosTz5tukXhdrv51re+xY9+9CO2b29I3aZpGn/729+aPMbr9fKnP/2JH//4xyxZsoTLL78ciIX03nbbbYgIJSUl9cLTGjTl02+nCVwsqGEK7WqF8YGOvCaYG2wqw2WoJxUhLYhrg4e8/j0onleI61U31VTEKney+gwJxSRTKGLlpZqEzGFJnvUAMFTzV6RG1/lJ//5U79/PJstiu21jx9cWzdEV4z0a04Fxlk0nUXzXo7HYtOqjR23biR5NCh06dOBnP/sZTz75JJs3bwZiFW/OnDmsWLHihP0Nw2DGjBn8+Mc/brRd0zTuueceAJYtW9Yo61Sq0XW9YXTbFiQYv6U1kDTBukiwB4N2lYZrgY79oo21Uyi3SlAvK4p9hUReDGPujzsmiYCdiiG85JJyCxPXS0nByRKLtCMnJkW+YeBA9h06xNaCgtiYWXxRos6G4nKPxlyluCRi09m08dkQNWyyvY0b8W29y1FHmxYKEUHTNIYPH86DDz5IYWEhr7zyCpZlMXToUB5//PETjqmtrWXcuHEopRoF3CilGD16NAAHDx4kGDy9tS6SQSOffhsk0ugxHnNBTgNrhI01EIzrddxPKcwXLOxCIRQMwP6E5rWAqnIhttUovqJlNJV8s32geTMb3qTA9PoiRagpKaFOKn6Rk8MzgQCl+/bFuiThMIaCHm6N670aN1kwJGTitxoqmEr4a4+0aaGora0lIyOD6dOnM2bMGF555RW6dOlCcXExZWVlHDt27IRj8vPzqa6uZs6cOdx3333nwOoTSRQKETghd03i3eMDc5iFegCML+sYjyrMNyzsY0L9nWoK/JtCO5aGfU0YOlmxxLpNldescS34Qm2FeKvQFohIcnxeG5WhGi7ljlCINMNARLDKy4FYWo8sDfoZMYGYawkDak3cVtN5OOscw9ojbVoodF1n2rRpmKbJ6tWrmTZtGg8//DA///nPqays5KGHHmLatGn07NmTUaNGEY1G+dGPfsS0adO48MIL20yz7oQowZPd0YkZldwQHWGh/guMG3S0RwXzTRvig++yJYj8UENNccMXDLjURLpZ4JEzS4zbThKnNIVSsRajBYTssx/QrJsKDWmQb2hss4VwwuWpm5L3KsjTFSMNxVW6Yrot9K4xcdmnvuxNiYSTuCYJ+Hy+Jmcu5s+ff8K2G2+8sTVMahG6rjeMiQhnNJMhXoheZqG7NfQdGtbGhOpQayOLQrBGR13mQs0y4DIL6W2CfrrpnVQTr9oJrlj2nJY4tyZSd3xAV+zUFSs0xRIFyyJ2I6FI02CIoRinKa7UYKIJuWELLb5Pu7t+Z0CbForzBbfbjadupSkbCMvp3dl1d54GZAsqp2FAoo97ICI2BeZBzOIoMt+C5QbqEh11rQe50oaeUdCaEYz23PXQG8T3ZJGvp6JutqTU0FhrKD4UWG4L26M2FZY0aqH4Fdzk1fiaBUNMIduSMxaI9iwkjlC0ApqmNZ5lacECvkJD2LNXS6NsfjGSbuPflE7OTzpxOLIXu9BEFpqwUodXdbRbfNjXRKCTGROEpu7U9tHybZK6fBQNnpnNf5n6dHsKjrk0PnRrLLCE9VGbQlsInKT/0kVTfMOGi8P2SS9ls/ZKwyJD7Y1mnydKqSeUUkVKqa0J236rlCpQSm2M/81M+OznSqk9SqmdSqmrU2V4e6KRH0VL28kJx+lKp2pCBdWXVVJ9VyUF+/bT+64B5Lq6xGuABe9FsH8SQn1dR3vDD9V6g0C105v1BNxeoPmvIwl/loKDXp2H0lzcqhQ/CFjMD1nsNeMioeno3Qfimn4zWt9hoMXGQdJ16GZLi0UCQInCddzRbWUcrTlOp+H5FHBNE9v/W0RGxf/eBlBKDQW+AAyLH/Owqhtx+hyja1rj3IgtqaiJc2uJg54eG7N7lP0P76S09hgXXjIWdwcvuqVDqY28Hcb+ahjtm17UB36o1hoHRrRn0YjHgYsIpt24PdFIHIAaTbHeb/DbDDczgHtqonwctii1BVPpZCudjl0HMn3iTIIFu6ld8jJfyu2K7kuvLzMZWb29evvsgjTb9RCRZUqpPqdZ3nXACyISBvYrpfYAlwAnekZ9nkhYLUziedvONCqh2RQUeuxv86o1aDU6facP4nDRXmS/EK2MYD9fC+/oaHN9yK0mMtKEbBtlq3Y88dHgmWnJidoX0qBIU2wxNBYaGgsjFkcCZvxzBR4vvVB06tCVd4oO0rFwNxTujhciPLN2CWuAHYBlJ2etknbSgDiBsxmj+K5S6svAWuDHIlIOdAdWJuyTH992Akqpu4C7gDYT5ZkqGg1mQnyeLHW100632LtiG2mrM/A85CP8cYjQgQBWuYn9VC0sNVAzXTAVWE2Df0Z7w59W/zKWuEZhI9Tqir26YpWh8Y7AiqhFcciiLpc3/gy6ZWQzTWl8PRxgauHeVjFXANNu/Muf79OjfwP+g9h3/g/gT8CdZ1KAiDwKPAowduzY9nG1Wojf7yc9vXETtjWa/LWXVFP7TDWZC3JQnyk6PphHac0x5KCJ/MNCLTCwa6MQihnT3n4EFZ/1sAT2A+vcGrXAcuBjga0Riwoz3iVRGiqnC78sL8JruOjvdnPL4T2tbrPZ3i5ynBYJhYjUu0QqpR4DFsbfFgA9E3btEd/2uaZuDQcgNqAYUSlvVSRSdV05XAeh0QG0Ap2cb3WiJHoUOdLYRTQpK623IhIPW7eAZabNQV2jVoQjibMXmoHWtS/3VpdzSTjALLEwqkqhqvSMzmURGwg9W/R22vVo0Sy6Uqprwtt5QN2MyBvAF5RSHqVUX2Agscbt5546z0wloKKcsRthMrLf1cyowrrDpGJTKWm/TidNy2y8ww7IuSfn7E7Silg71ta/rrBhU9RmT93shdLRug9kztCxbCnO597aCq6rrWxxE9oCIsbZOZ0owKUdF13TTgYtmr1uSqnnifVmOyql8oHfAFOVUqOI3b8HgG8AiMhnSqmXgG3E/A+/IyLt6zGVIo534W5Re6IhSqnlhrjAHBrB/LcIY6svpfD/CiiIHASEaChKxX9X0OmxToQeC1EzqwbxnuVQf5KJKoUpMO2Ci6jcu6nxh0rh0V14eg3j4L6N6Ef24irchzdZodzqzLzjmyJx0LU9cTqzHrc2sfnEsM2G/X8H/O5sjDofaSQULcjb1jjyMAk11w1r//QpwypGU/xsIZFoLIGKmEJxRTHaTRqDXBewe/Ue9ByNSO/WS8/XFGEU+brO/3TpxcORKPbu9ZCQazPLcNOl7zD+dfQAF+3bELtC0rZqZd3sTHvE8cxsJbS4445YxFYONznjx1ND1yNJd5uCz57YgHpPi81PeRSqq4GUWdjVNjuiOzFGG3Tr1pWCxwsxehsEh7ReeD7Ahx27EawoZQ/wg/QcpPBAI4EAQNP5ilL8z+4NKbPDjv+drR+F57iux/k+6+FwhtQtVCxRwd4G2lYNe4wVS0h7GndfY01JTV9A5Rlov/Ai+RbyjoVsjWIGTA4cOYR/pg//ZD/+eX5qbqwh3CO1KdyWZHVkczjE/bl5VNTWIMEqqDiKrml08fnp6vGwLxikPBSKpcTTUuXXF+skCnLWg5kCRNtWI+e0cYSiFVBKkZGREXtjg7XeRv+1hvFVDftqwc6R08tqkuwWxfF4BfuSCHKzhbpGR3vfA68J9tYIgWiQ4LIQWZ9kob+nc0GPgez6v91Jv4O2uTz80ZPGcttmp9iwcz0ALl2nV1oaU3w+Lrdt+gGPdOnM0wcPkdqqlzia1IYGa1oZRyhagbrUfUuXLmX79u3YtTbWhzZqJ+hv6ej/D6ITLXBx8ntRI+HXStENq6uYDZkmMs5Ehmmoaw30N/3Iiyb2zjAVZgXqbUWhdpS0LX76D+3P5n9sabK4M7HymvHXUL1lNeXBSraHasCMeYG5DIMhWVlc6/MxPRJhUE0NueEwBrAiKzPB1TH1z+mzv+qC3Q5SGDZFew4ybldcdtllPPfcc3zta18jNzcXTJDDYL5kYd1u437QQD+YEIdxnFOWMhTKlWIjdRVzBYfYnZFhIxdGsH5Ui7wg6D9JQ/V0I5pQbVcTWBFk5zM76dOjNwP/MuCkg7RN+ZfVxWB8fcAoumZ2ZvH6j1geqGC7bYEZwe9yMaFzZ/6rVy9eBX5RVMTkkhLyamtxmSZKBEOSMxF0OggQbeFp6mNONEVNwnbbttvNGIUjFK2Ey+Vi+PDh/PGPf+Qf//gHV155JRkZGShLYecLkftN1E3gft5AlSjqfZ8SW72t3fKtO6dfkGFhrN8E0F5xod+ZAXkG4oJwNMKBgoMc/NFBxmaMIeOTDFzHXKhSRTjuG/6DsVfyaafuCFDk9nJMaTzmz8Kb1YXH927maFUREgniVtDF6+W6vDye7NaN1yMRvnvwIP1KS/FHImi23egyaHWVLBlOJs1gy5l7utcJhA0ENFjh1VgTz4QjIliW1W6Ewul6tAJ1TjVKKTIzM5kzZw6jR4/mX/96lpdffoVdu3YRCAQw19qoH9oY1+rYdwj2aBvJJFYzLFKzeEWzxie89tpYF9eihhnoN3uRZ23kkwhSYBEJR1kbXI93ipchrkEU2kcpltiiR9Fta9kaCaIpjSsumkZ482qkthSoRFOKNJeLPl4vl6alca2uM6GmhuyiIlRcGJpEBC1JCwefLuo02xOJOS/KNcVOl2KJofFCxOZAJPYjapqGz+drHFXchnGE4hygaRq9evXihz+8mylTpvLSSy/xzjvvsH//fqKlUaLPWmhrFPqNOjJbsIfFFaItPHwUiN/EuqIGdbGB9qkbmQ/yiYkciBIKh9gc2droEAlU8C2lx2YnViwCwNB1uni8DHO7mODxMEMphldX4wsEUPG0983R0ByWFLYoEmP6T71nokAccWms0xUfISy2YG+tSV3ydY/Hw/Dhw5k0aRJ+vz8lVicbRyjOEUopfD4fEydOZPDgwVx55ZW8/vrrvPfeexQUFGBvs5H/stDe19Cv11C5CilOsVIoTq8zGm//S5aJdY2FGmugVhuohQbynokcinBC2IhYIODWdfqkpTHB42GapnFJJELvykp84TCcpkDUoUE8dD/1CGCewjgBwjrsMzRWKFiiFCss4UjUJho3MC0tjSFDhnDZZZdx9dVXM27cOHRdbxdu3I5QnEPqbpAOHTowY8YMRo8ezeWXX84zzzzDJ598QiAQwFpuo7aDylLI0RRXCY0zG7VSgC5I5ygyw0SN1eF6A31BOvbLYaSkwZvTbRgMzspirs/H1GCQgYEAnSIR3NFoy4Ze4oOZsdekfowCsI6r0HVnDOuK3R6NhQrejdrsMIUSq0ErMzIyGDNmDNdeey2XXXYZ/fv3Jzs7u910O8ARijZB3WJF3bt354YbbuCSSy5h/vz5PPLII+zfvx8pE6SsoSKkbABMqZZlVqkTjDwTOllYY6MYF2Rg3lsFYRuf281dXbrw9UCA3sXF+KJRdLs+O8RZkKAUKbomiYsKHp8YJ6rDZz6d5xW8E7Y5YAq1CcsG+P1+xo0bxxe/+EWmTp1K165d8fl87aIFcTyOULQRlFKICB6Ph/79+/P973+fK664goceeoi33nqL0tJSRAQRIWjVQI2gu3WstGQP6LWwwtXd+7pAtoUMt8GtIAyjcnK4MxBgSFlZ/UzFWVcVEVx6fBVwaUG24tOmIYtWVMXGH2p1xUavzgsavBG0OBaV+taDruvkZmczZswYvvzlL3PllVfSsWPHE1ata284QtGGSJwd8Xq9jBkzhoceeogbb7yRxx57jLKyMo4ePcq+fftQvdyM6juOzW+tRu+gE+wSOHsDRM4+35tq9A8AeZoiOxpFO8MxiObokJ6OYRhYkVQGrMUEqErgTaAkXedtgUUhi+J4FhqlFF6Ph7y8LkyaNJk77riDiy66iKysrCYXqG6POELRxvH7/VxzzTWMHz+ecDjM22+/zX333cfhw4dZt/8Tul7Yk9yZndn+P5sw+55lhUlVj0ZSU3j9MKakLmVYXcreGhv+VmPymIKgFY+9iU93Dxw4kAkTJjBr1iwuueSS80og6nCEog1Td6Ppuk5ubi4iwrXXXkthYSEvvPACO3fu5Ih5iNI3izGUm6wJHaj4VglW5ll0R1JR31RqvMWUSEpduF/xplMaDtYXHbFjTldKKXI7dGDUqFFcccUVTJ06laFDh8Yc6M4zgajDEYp2hFKKzp07893vfoeJEyfy7LPPsmjRIoqKipAF4H7TjXuVjwu7jWHVQ8taeJLk2NoaU5Z6iirl8uyOPOxL56PyEooROnXqhGVZVFVVkpfXlfHjx3PVVVcxYcIE+vbtWz9AeT4KRB2OULQzlFJkZ+cwZcoUhgwZwowZM3jkkUf49NNPqQqXo83X2e3aTk55J8r/VXyapSa4QifJ+7NRlUnBjIQClJ1gbBJOUaEbXNVnBCUFu9gfrIVwCK/Xw9133023bt3YtWsXkyZNYtiwYXTq1Amv19tgz3ksEtBOhGLRokXcdtttACxZsoSbb76ZsrIydF3Hsizuv/9+3n//fT744AMMw8A0TWbMmMGzzz57ji1PPondka5duzJ37nWMHj2a5557jieeeIL8/HzKosVoL2pkvZeL+6duSn54FGkUQdWYRtHrbcH78zTRbTvW/Wih0RYqNnYrwujewygo2E3FgS1gmSilSEtP47bbbuPrX/86WVlZWJaFy+Vq9zMYLaHNB4VFo1EKCwspKyujrKyMI0eOUFpaitvt5rXXXqOsrIxQKER1dTVlZWVs2bKFsrIyiouLqaysPNfmp4y6G9TlctO/f3/uvfdennrqKebNm0dOTg4IVBaXUv6zEkZljSdzafbptRba0X3vtyxa4rJkKkW+28cDg0biHz4Rj+Hhs4OfUWFGcGmx7t2sWbN4/PHHefDBB8nNzcXlcuH1eus9Kc/3rsbxtPkWxd69e/na175W//7aa68FYN68eU3+UIZhcPHFF7N48WL+8z//kwceeACIOSl99NFHAGzfvp2ePXuecGx7I3E61e12M2XKFEaOHMmrr77KP//5T7Zs2UJlZSUbgitIuzoT9bqGt5OP4LjakxTYisYngZaY+0lGDodNky8PGIW5cx1EYtPKPp+PXr16MWbMGGbPns20adPo1KlT/Qpvn3fatFBEo1FeeOEFevfuTV5eHqtWrQJize5XXnmFFStOXKnQ5/Px9NNPM3To0EbbbdvmpZdeQkQ4cuQI3bp1a5Xv0FrUPeFycnK44447mDBhAq+++ioLFixgx44d1AarULM1MjpnIfcJ3uE+Ki49bm2LJHY9Tmdl8bOlLtbjdHg3PYd9oVp+ktuVQP5e2PJxbHozK4sLLriASZMmMWvWLC688EJycnLaTQxGa9GmhSIcDvPv//7v9OnTp1EWa9u2+eUvf8msWbOaPOb+++8/Ybuu6zz88MMAvP766wSDrZsktjVxuVwMHTqUHj16MHHiRF5//XXefPNN8vPzKSo6gu9babhGuuk8rTthCVJVUZ70aq1aoXnitm20ZirzOpeXp3UXbymNfQAHtsUGhHNyGD16NNOnX8nkyZcxbNgwsrKy6o9zRKIxbVoofD4f77//PgDPP/88K1as4OGHH+bee+/lySefbFIootEozz33HBMnTmzUZfm8kHiDZ2VlMW3aNEaMGMGVV17JE088wZIlSwiGagltDOLb7McUs3HsSDuqH429Mxq+gw3MunQG0Y0rKAzVsM22IVQNQHZ2NlOnTmXOnDmMGzeOnj17kpaW1qgb53AibVoodF3n8ssvB2D16tiCY2PHjsXtdlNcXMyNN94I0GhgacyYMQB06tSJ/v37nwOr2waJsyNdunSp9xp88803+ctf/sLu3bsJWDWNDwoLqkqnkSNlG603Ao3yVjzddQATbIv5nbuz6sAuDq7/OLbkoNhomkaHjh2ZOnUKt9/+ZcaNG0dWVhZut/tzNyjZUtq0UCTy05/+lB/96EcYhkFBQePlTHVd5zvf+U6jJ6Pz48domB1x0a1bN+68804mTpzIo48+yquvvkpZWRkiQjQaRQ6aaP/tRvuFF3tAGNzSJgWjbiilVins+G9ecXQ/t+kGVvEhJL4ymMvlonPnrsycMYPbbr+dkSNHkp6e3qgb69wnp0e7EQpd1+vnr91ud5OfO5ycRMEYPnw4v/vd75g2bRrr1q0jGAzw7LP/oqSkBOvlANouL/r/S8e+JhQLHXe1DecKAVCKiK5T7PfzYjRKdTi+vohYmKaFpmmkZ2TQrVs3pk6dyi233MLFF1+M3+93Wg9nQbsRCofkUFdZMjMzmTdvHnPnziUYDGKaFs888wxVVVXYa4OoPQbaBx7kJgOZaCKdzfgKy61rb71EKUXA7eagz8cat5t3dJ2FhYUopejRowemGXOSGjx4MFOmTOGKK65g5MiR9eMPjkCcHY5QfE5JrDxpaWn8+Mc/JicnhwULFrB9+3aiFVGsl0zUcjdqpgt1g4FcHEUyzVYTCwFEKWr9frb5fHysabxvWayvrqYkFMIWYeDAgdxzzz3105ljx46lf//+eL1eRxySiCMUDgD07t2bu+++m8mTJ/Piiy/y1ltvcezYMeRQBHnSRH1qoK51o27VsQdFYt2RZnJI1nOGFVYA0TSq/H42ZGaywLZZHgyyJxSiMhLBjif4ueCCC/jhD3/ILbfcgsfjAZwuaKpwhMKh/slbN3U4bNgwpk2bxt///ndWrlyJGTaRrRHkgIn2kQv9a+nY14eRrMhJxeJMn+X1aeaUoiozk0+ysngxFGJFZSVHwmFCpokQG5+68MILufXWW+sD49prern2hCMUDvUopTAMg65du3LzzTczefJknnvuOR577DEOHDiAXW1jrwjDFhN9kR9+7MYaFQC3feoFik4RPVq/SI6mUZGRwbLsbJ41TZYVFVERDmOJxDKW+/0MHTqUW2+9lXnz5tGtWzcMw3BcrFsJRygcGlGXu9MwDHr27MlPfvITpk+fzl//+lfee+89ioqKsKotrFeqUZ+4MO5Mw749gt0nAp4zWyBHlCLocnHU52N5Tg5Ph8OsPHqU2vhMhmEYdMzOZsSIEdx0003MmjWLbt26fS6jN881jlA4nEBi5dN1ndGjR/PnP/+Zd955h2eeeYZ169bF/C+ORjH/ZKJ97EX/qg/78ijSzQTt1C0IS9epdLvZ5/Pxgc/HG5EIGwoKCERjqfy8Xi95eXlcdNFFzJs3jyuuuMIJ0DrHOELhcEoS1x656aabGDVqFG+99Rbz589n06ZNBINB7E+CqF0G6koX6kYDudSCsFYf1i7xZQBsl4tiv5+1bg8fKfgoGuWzoqJ6gfD5fPTv35+JEycyffp0Jk6cSJcuXeodpByROHc0KxRKqZ7AM0AXYg+ER0XkL0qpDsCLQB/gAHCziJSr2K/5F2AmEAC+IiLrU2O+Q2uQ6Kw1dOhQevfuzaRJk3jjjTdYsGABu3fvxjpmIi9aqLUu1BQDCdgQjinF4WiUNdnZLPX5+MA0WRkKcSgYIGSaQCyB8IgRI7j66quZPHlyfQapui6GIxDnntNpUZjAj0VkvVIqA1inlHoP+Arwvoj8Xil1L3Av8DNgBjAw/jcO+Fv8X4d2TqLfxbhx4xg8eDBXX301jz/+OIsWLYp1R3ZGkANR0BTE09lvKS/np4EAAdumLBIhGk9hl56ezujRo7npppuYOnUqvXr1qnexdsShbdGsUIhIIVAYf12tlNoOdAeuA6bGd3sa+JCYUFwHPCOxwIuVSqlspVTXeDkO5wFKKTRNIycnh8mTJzN48GCuuuoq/vd//5eNGzdihk0SPSnClsX+QMO6I2lpaYwfP57bb7+dyZMn07Vr189V/sn2yBmNUSil+gCjgVVAl4TKf5RY1wRiInI44bD8+LZGQqGUugu4C6BXr15narfDOaZudkTXdfLy8vjiF7/IxRdfzOOPP86LL77I0aNHMeNdC4jNYGRkZDB27FjuuOOO+hW0nACt9sFpC4VSKh14FfihiFQl/qgiIkqpM4ocEpFHgUcBxo4d2zaijhzOiONnRwYPHszvfvc7rrrqKh577DFWrlxJdXU1HTt2ZMyYMdxww/VMn34V2dnZTvxFO+O0hEIp5SImEv8Skdfim4/VdSmUUl2Bovj2AiAxIWWP+DaH85i6Su/xeLjyyisZMWIEy5Yt49ChQ4wYMYIxY8aQm5vrjD+0U05n1kMBjwPbReTPCR+9AdwB/D7+74KE7d9VSr1AbBCz0hmf+HyhlCIvL4+bbroJiXtWOhmk2jen06K4FLgd2KKU2hjf9gtiAvGSUuprwEHg5vhnbxObGt1DbHr0q8k02KHt44jC+cfpzHp8wsm9+K9oYn8BvnOWdjk4OLQh2vwCQA4ODuceRygcHByaxREKBweHZnGEwsHBoVkcoXBwcGgWRygcHByaxREKBweHZnGEwsHBoVkcoXBwcGgWRygcHByaxREKBweHZmnzyXUPHz7MnXfeWf/+oYce4he/+AVVVVX12775zW+yZs0a1q1bV79t4sSJ/Pu//3ur2urgcL7S5oWitraWJUuW8M1vfpN77rmHbt268dFHH6FpGg8//DA33XQTM2fOZMOGDSxZsqT+OL/fXx/i7ODgcHa0m66H1+slJyenPjNzTk4OXbt2PWG/iooKNm7cyMKFC/n1r39dv11EqKiooKKigkAggJxi9SoHB4fGtAuhyMzM5IUXXiAnJ4eXXnoJgO3bt5OWlkaPHj0a7et2u3G73di2jWVZ9dsty2Lq1KlMmTKF+++/n3B8NSoHB4fmafNdj4yMDH7xi1/Ur1z9pS99CU3TWLhwIRMnTuTaa689rXIMw2Djxo0AvP766wSDwRRa7eBwftGmWxSRSIRHH32Unj170rFjR7KysgCwbZtvfOMb7Ny5k7///e+Njrn//vt56KGHGDRoEFdccUJeHQcHhxbQplsUkUiE++67j65du5Kbm8vWrVt58MEHeeCBB6ioqOBXv/rVCcc88MADAMyZM8cRCgeHJNGmhcLv97Np06ZG2wYMGMCcOXMarRnRrVs35s6dS3V1df22zMzMk5ZbXl7Ob37zGx588MHkG+3g0AYpLCxk2rRpLT6+TQuFpmlceOGFJ2wfOnToCds6dux42uValsW3vvUtvvWtb52VfcmkoKCAu+66i7feeutcm1LPpZdeyqJFi04puq3N7373O0aOHHnaY1OppqSkhJtvvpmlS5eea1MaMXjwYLZt29ZogaW0tLQWl9emhSKV+Hw+srOzz7UZ9VRXV2MYRpuySdd1srKy6seG2gIej4e0tLQ2c52i0Si6rrcZe+pQSpGVlVXvTnC2tOnBTAcHh7bB57JFMXToUCKRyLk2oxHp6enccMMN59qMRnzxi1/E7XafazMaMX78+Da1Vq3P5+OWW24512acwNe+9rWkeiWrtuChOHbsWFm7du25NsPB4XPN2LFjWbt2bZPq8rlrUWzevJnvfve79e9feOEFunXrlvLzighXXnkl0WiUyy67jPvvv5/f/va3jQbBRo4cyRVXXMGf/9ywcmNaWhqLFi1KmV3f//736x3RAKZNm0bv3r156qmn6rd16dKFe++9l7vvvrvRsUuXLsUwknsLrV27lh/96Ef175VSvP7661x33XWN9nv66af51re+RSAQqN/205/+lNmzZyfVnjoKCgq49dZbAfjZz37GwoUL+eyzz+o/v+qqq+jYsSPPPfdc/bbu3bvz/PPPp8QeiLX48vPzgVhLa9SoUY38inJycnjggQdOGLR/77338Hg8Z3YyETnnfxdddJG0BkePHpWOHTsKULf6unTu3FmCwWDKz23btni9XgFk3rx5IiJyyy23CCCbNm0SQC677DJ5+OGH6+1TSklmZqZYlpUyu6ZNmyaapsmmTZtEKSVer1fS09MFkCVLlkhGRob06tVLlixZ0sgupZSEQqGk2/Pee++JUkr+8Ic/yLhx4wSQLl26CCDXXXedfP/73xdAtm7dKhkZGdKzZ0957rnnBJC///3vYtt20m2ybVt27dolgADy2GOPyfjx40UpJRs2bBBAbrvtNrnnnnsEkI8++kj8fr8MGDAgpb/dwIEDxefzSX5+vpSUlMh//ud/CiALFy6U3Nxc6dy5s6xYsaLe7rp7vqampsny4vWwyTr6uRrMtCyLkpIS7rzzTsLhMFdeeSVFRUXNH5gElFIUFJy4qHtWVlaTwW2LFi0iHA4TCoUYM2ZMyuxavHgxoVCI4cOHs2TJEkKhEDU1NWRkZNC1a9cT+rl//etfCYfDdOvW7YQ4m2Rw+eWXU1lZyR133FF/7mPHjqHrOp07dyYjI6PR/rquk5eXR1paGt/+9rf59NNPk25TKBRiyJAh9e+/8Y1vsHLlSjp06EBeXt4J+3fu3Jnc3Fz27NlzQksoFXg8HlwuFxAb6+ratesJsx2///3vCYfD9O/fn+7du5/xOT5XQlGHUgqXy9XqIehNNdM//PBDcnJyGDlyZKPtuq7X758Y3JYKmwzD4KOPPuKKK64gJyeHbt268cQTTzB06FBGjRp1gl111y7R6S1ZaJrGW2+9xaxZs9i6dWv99pEjR/Loo482ecy0adO4//77sW07JVHBGzduxDAMBg4cCMRCCAC2bt160unHnTt3Aqn97QAGDRpEp06dmDFjBvn5+Tz00EOMGTOGkSNHNrq/NU07q9/tcykUbYm33noL0zQbJedpbebPn8/06dPJzs7mvvvu4+tf/zrLli2jvLycu+66q9UF9Qtf+AJr1qzhZz/7GT6fD4CysjI++eSTJvc/cuRIo6RFyWb69OlkZWUxd+7cRttfffXVkwrTyy+/nDJ76pgzZw7Lli1jzpw5LF++nP/93/9l+fLllJSU8PWvfz2pv9vnUijWrFnDvffey+7du8+1Kfzyl7+ksrKSH/zgB422/+Mf/+DnP/85hmHwwx/+MGXnf/TRR/nKV76Cy+XiT3/6U/1A7//+7/9y+PBhvv3tbzeqDK+//jr33nsvlZWV/PKXv0y6Pbt37+bee+9l9erVdOrUqf6JfeDAAf7v//6vyWO2bt3Ks88+y7x58+jTp0/Sbbrvvvu4++67KSkpAeCGG26gV69efO9736tvXRzPt7/9bXJzc/nKV76SdHsAnnzySQzDQNM0unTpUr/90UcfZd++fSfY9vbbb3PvvfdSWlraZIxUs5xs8KI1/1prMDMYDMrvf//7+sEdQB599FExTTPl57ZtW+bMmSOA5OXlyezZs6Vbt24CyFVXXXXCYGbdX2ZmZkrtmjJligBiGIbMnj1bZs+eLRdccIEAMmXKFDEMo9FgZuJfOBxOuj2LFy8WQC688ELp0KGDAPL0008LIN26dZOBAwc2Gsz0+Xwyfvx4AeSRRx5Juj2JLFq0SAD5xz/+IRMmTGj02yUOZk6bNk10XZcBAwakzJaZM2cKIFdffbUActFFF8kdd9whgEyePFncbvcJg5l1f4FAoMkyTzWY+bnzowgEAhw6dKj+fb9+/VrFqUhE2LVr1yn70H6/n4yMDI4dO1a/Tdf1+r5xKjh06FCjKcamcLlc5OXlcfjw4UbbBw0alPRuSW1tbaPzKKXo378/e/bsabRf3759OXjwYKOnZl5eXkpdqWtqasjPzycvL4/KyspGOU0yMzNxuVyUlpbWb3O73fTr1y8ltuTn51NTU1P/Pj09HZ/PR3Fxcf02wzDo3r07Bw8ebHTsBRdc0CgGpI5T+VF87oTCwcGhaU4lFJ/LMQoHB4czo1mhUEr1VEp9oJTappT6TCn1g/j23yqlCpRSG+N/MxOO+blSao9SaqdS6upUfgEHB4fUczr+tybwYxFZr5TKANYppd6Lf/bfIvLHxJ2VUkOBLwDDgG7AEqXUBSKS2gllBweHlNFsi0JECkVkffx1NbAdOJVr13XACyISFpH9wB7gkmQY6+DgcG44ozEKpVQfYDSwKr7pu0qpzUqpJ5RSOfFt3YHE4fF8Ti0sDg4ObZzTFgqlVDrwKvBDEakC/gb0B0YBhcCfzuTESqm7lFJrlVJrE6d0HBwc2h6nFSOslHIRE4l/ichrACJyLOHzx4CF8bcFQM+Ew3vEtzVCRB4FHo0fX6yUqgVKWvAdzgUdcWxNBY6tqeF0be19sg+aFQoV86h5HNguIn9O2N5VRArjb+cBdRE8bwDPKaX+TGwwcyCw+lTnEJFOSqm1IjK2OXvaAo6tqcGxNTUkw9bTaVFcCtwObFFKbYxv+wVwq1JqFDG30APANwBE5DOl1EvANmIzJt9xZjwcHNo3zQqFiHwCNOWt9fYpjvkd8LuzsMvBwaEN0ZY8M5tONtA2cWxNDY6tqeGsbW0TsR4ODg5tm7bUonBwcGijnHOhUEpdE48J2aOUuvdc23M8SqkDSqkt8XiWtfFtHZRS7ymldsf/zWmunBTa94RSqkgptTVhW5P2qRh/jV/rzUqp1CXjPH1b22TM0ClinNrctW2VeKyTJapojT9AB/YC/QA3sAkYei5tasLGA0DH47b9Abg3/vpe4D/PoX2XAWOArc3ZB8wEFhEbnB4PrGoDtv4W+EkT+w6N3w8eoG/8PtFb0dauwJj46wxgV9ymNndtT2Fr0q7tuW5RXALsEZF9IhIBXiAWK9LWuQ54Ov76aWDuuTJERJYBZcdtPpl91wHPSIyVQLZS6sQU4CniJLaejHMaMyQnj3Fqc9f2FLaejDO+tudaKNpDXIgAi5VS65RSd8W3dZEGZ7OjQJemDz1nnMy+tnq923TM0HExTm362qYqHutcC0V7YJKIjAFmAN9RSl2W+KHE2nJtduqordvHWcYMpZomYpzqaWvXNtnxWImca6E4rbiQc4mIFMT/LQLmE2uiHatrVsb/bZ1VhE6fk9nX5q63iBwTEUtEbOAxGprA59zWpmKcaKPX9mTxWMm6tudaKNYAA5VSfZVSbmIJb944xzbVo5RKU7FkPSil0oCriMW0vAHcEd/tDmDBubHwpJzMvjeAL8dH6McDlQnN6HPCcf3442OGvqCU8iil+nIaMUNJtqvJGCfa4LU9ma1JvbatNTJ7ihHbmcRGafcC/3au7TnOtn7ERoc3AZ/V2QfkAu8Du4ElQIdzaOPzxJqVUWJ9za+dzD5iI/L/F7/WW4CxbcDWf8Zt2Ry/gbsm7P9vcVt3AjNa2dZJxLoVm4GN8b+ZbfHansLWpF1bxzPTwcGhWc5118PBwaEd4AiFg4NDszhC4eDg0CyOUDg4ODSLIxQODg7N4giFg4NDszhC4eDg0CyOUDg4ODTL/weqb6+TDNgRRAAAAABJRU5ErkJggg==\n",
43 | "text/plain": [
44 | ""
45 | ]
46 | },
47 | "metadata": {
48 | "needs_background": "light"
49 | },
50 | "output_type": "display_data"
51 | }
52 | ],
53 | "source": [
54 | "rows, cols, _ = img.shape\n",
55 | "\n",
56 | "for i in range(rows):\n",
57 | " for j in range(cols):\n",
58 | " B, G, R = img[i, j] \n",
59 | " if B > 100 and G > 100 and R < 50:\n",
60 | " B = 0 \n",
61 | " G = 0\n",
62 | " R = 255\n",
63 | " if B > 100 and G < 50 and R > 100:\n",
64 | " B = 0 \n",
65 | " R = 0\n",
66 | " G = 255\n",
67 | " if B < 50 and G > 100 and R > 100:\n",
68 | " B = 255 \n",
69 | " G = 0\n",
70 | " R = 0\n",
71 | " img[i, j] = B, G, R\n",
72 | "plt.imshow(img)"
73 | ]
74 | },
75 | {
76 | "cell_type": "code",
77 | "execution_count": null,
78 | "id": "5b96834c-53f8-4806-830d-c86b56b8518a",
79 | "metadata": {},
80 | "outputs": [],
81 | "source": []
82 | }
83 | ],
84 | "metadata": {
85 | "kernelspec": {
86 | "display_name": "Python 3 (ipykernel)",
87 | "language": "python",
88 | "name": "python3"
89 | },
90 | "language_info": {
91 | "codemirror_mode": {
92 | "name": "ipython",
93 | "version": 3
94 | },
95 | "file_extension": ".py",
96 | "mimetype": "text/x-python",
97 | "name": "python",
98 | "nbconvert_exporter": "python",
99 | "pygments_lexer": "ipython3",
100 | "version": "3.7.9"
101 | }
102 | },
103 | "nbformat": 4,
104 | "nbformat_minor": 5
105 | }
106 |
--------------------------------------------------------------------------------
/lesson7/4.ipynb:
--------------------------------------------------------------------------------
1 | {
2 | "cells": [
3 | {
4 | "cell_type": "code",
5 | "execution_count": 145,
6 | "id": "b5b86248-9621-4525-bf5e-1fe60a69c0d1",
7 | "metadata": {},
8 | "outputs": [],
9 | "source": [
10 | "import cv2\n",
11 | "import numpy as np\n",
12 | "import matplotlib.pyplot as plt"
13 | ]
14 | },
15 | {
16 | "cell_type": "code",
17 | "execution_count": 146,
18 | "id": "f50d9063-f7f7-4ace-912b-8febeee1859f",
19 | "metadata": {},
20 | "outputs": [],
21 | "source": [
22 | "img = cv2.imread('3.jpg')\n",
23 | "rgb_img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)"
24 | ]
25 | },
26 | {
27 | "cell_type": "code",
28 | "execution_count": 147,
29 | "id": "38ecd978-346a-4422-b8ac-a29003cf0d3a",
30 | "metadata": {},
31 | "outputs": [],
32 | "source": [
33 | "gray_img = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)\n",
34 | "thresh = cv2.threshold(gray_img,150,255, cv2.THRESH_BINARY)[1]\n",
35 | "detected_edges = cv2.Canny(thresh,9, 150, 3)\n",
36 | "kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (3,3))\n",
37 | "close = cv2.morphologyEx(thresh, cv2.MORPH_CLOSE, kernel, iterations=1)\n",
38 | "circles = cv2.HoughCircles(close,cv2.HOUGH_GRADIENT,1.2,20,param1=50,param2=25,minRadius=3,maxRadius=35)"
39 | ]
40 | },
41 | {
42 | "cell_type": "code",
43 | "execution_count": 148,
44 | "id": "a5727f98-4b8e-449e-842f-df5f82e8aba3",
45 | "metadata": {},
46 | "outputs": [
47 | {
48 | "name": "stdout",
49 | "output_type": "stream",
50 | "text": [
51 | "5 1\n"
52 | ]
53 | },
54 | {
55 | "data": {
56 | "image/png": "iVBORw0KGgoAAAANSUhEUgAAAW4AAAD8CAYAAABXe05zAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjQuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/MnkTPAAAACXBIWXMAAAsTAAALEwEAmpwYAAC2M0lEQVR4nOy9eaAdR3Xn/zlV3Xd7q/S0b5ZsS7Llfd+xjbHBZjEQAhgwZpkQEkiAYfKDZDIzSSCTTCYTyEIgBEhMYnYM2AbbeMX7bsv7JkuyLWtfnt567+2u+v3Ry+3bt+/ynmRbsu+xr153dW1dXfWtU+ecOiXWWrrUpS51qUv7D6lXuwJd6lKXutSlqVEXuLvUpS51aT+jLnB3qUtd6tJ+Rl3g7lKXutSl/Yy6wN2lLnWpS/sZdYG7S13qUpf2M3rZgFtE3iIiT4nIsyLyxZernC51qUtder2RvBx23CKigaeBc4EXgXuBi6y1j+/1wrrUpS516XVGLxfHfSLwrLX2OWttBfgBcOHLVFaXutSlLr2uyHmZ8l0IvJC4fxE4qVlk6XEtg4Xsh9GCQFL3rwY1lD3FymRFl3ScPXjBKSfNSLDX2ncvZdTd2Null4328c41UsVO+mmEAF4+4G5LIvIJ4BMADOSRTx5X99xaiS6iBPX3zcgmsdCAgDXQiJBRlCl8vHTZreoS1qNOFNVQlgWx9XlFUbLytu3KbNc2Ns6/oW7xc5MIaLEgS9S3sWUNttmgyIwfZZn9zqrZsw7yaVZWl17vZLFRX09jzL5CP1/f9NHLJSrZACxO3C8Kw2Ky1n7TWnu8tfZ4etyXqRqvJtl6sGkGPO3AuEtd6lKXUvRyAfe9wHIRWSYiOeD9wBUvU1n7JiWxuCUwp8Hd1od1qUtd6lKKXhZRibXWE5FPA9cCGviOtfaxztNnhrZJNN24U6RmIoysjDvluJvdd8KJN823WVob/d95Gc3iJu6n88lq2bSe2DqtYtfTZZdeL/Syybittb8CfrUHOZChuQv/NpdFSSQzrkOnvUAdgWjqOp1Ewgc2HblJmqnUv0nT1BXZLM+6sNZyPknnlWzvVmV0qUtd2mv0qiknOybp3JykBjk2HdA0frtcM5V408wLa2tImkqbDu0ovynQdFqx47wyKvtqqnn2MRVTl7q012nfB+5Xk2zKNmJvLMVtlzPtUpe6tGfUBe5Oaa/IT5vJvLs8Ype61KXOaR8G7ozF/VT3u9gmgt+0gi47cf3f9HVjdhlxOqu7TafptG6tKtKgR2z2Hq1Kqredl3T8UOwznTmtpfgpqQPoNO+uYrJLryPah4E7Se2VkrWoLXZ47KW6NMq9JfjVKRdNJCCvSy0ZV003q0yFknLmVk3QsMmmXabhVQSm0mwC2Lsk08i6u27p0uuFum5du9SlLnVpP6MucHepS13q0n5GXeDuUpe61KX9jPYhGXew4aZebJreAt5Eilm3oSUZVzpTLtbllYrfcZp0+TZzE06jYyfqI7XcRJgVL9FGNnznZgrDKe/ETMvCbXOlYkdZt4nUmfl90/y6Mu4uvV5oHwLuiLKGX6fbRtIgLzTk1ykwxrk0hjUCUIYFSiJYmuGyzUoTJaqvd/MNOdE7G0AhDZNfKtoUFKF17y6db0TaE4qWgF0bkS51qTntg8D9KlEmZ94GtF9NE7S6vecQQF6X5+xSl14P1AXuNHWys3GfsRmORBnSZVG71KXXEXWVk0naV7jpjighFrLQ5bi71KXXD+1DHLfUTr0B6hVjTTjKBgWdCeNKfRqbFiukQY96BWMz/VsnLlTT5WTtgsySbbfKM5mtTbdL0GZiLTa5lSdr52djBZuWF2xkkqan0nRKHblaTbqHtZE0P/pl6CnqdBlpnUaXuvTap30IuFtRCzeuQN2OPis0qLiaYkftgaT2LzYeBTkVpV6Upn25jYlTR7TZUDEZexVMThIqy9lg52Uli02m6PBd9zpMZhYbgXcqLOGvtgvXXXq9UVdU0gF1HfR3qUtd2pdoP+G4Xx3aZyxIutSlLnUpQV2Ou0td6lKX9jPahzjuOilr/aNW7lnDuPWm1zalAEztAMzgpGtBTRSKWWkzq5vatdiJIrJd3erKiGTgUZRUYZGStZMi29Qre5fnFOJ3QrZmki6xgrldkuj7RiFdKXeXXl+0jwB3bav2lJNFZDMDGuN2uO26PqzzHYMvv0Sl3jFso+1Jh6CdmePejTutOjQ7ZrSBkkrLLnB36fVFXVFJO+rKubvUpS7tY7RHHLeIrANGAB/wrLXHi8hM4IfAUmAd8F5r7c49q+arRE1tobvUpS516dWjvcFxn22tPdpae3x4/0XgBmvtcuCG8L4tNXXclB0bknLO9F6MOoF3AnzT4Zny4XTc7KJrv2RdUtx5ndfAVq9j68tM1zXaQFT3vilPfQ2bjJoWRuO7R1lkeP9Lt3Fm9Vt4DWyMnHrfJjqDDpuuS116PdLLISq5ELg0vL4UeGfHKTMBK5Jlpqtq67zXiY32ZBgCBZcJ8sDUA59JgqAN7qOw6ZBNeP9rAHXazD8pAI2PFUu/QxNwS6aL07evb6PudwrAuzepZftE31y/YtXpUpf2F9pT4LbAr0XkfhH5RBg211q7MbzeBMzdwzIyqU4t1erw3Jep7LoN1kluu1Mf3mlqk0bIKHcPaKp57fUN5baW7ytUYpe69JqhPbUqOd1au0FE5gDXiciTyYfWWiuSfexrCPQB2A/kp1m8TeDlq7eujtYE3R2WXepSl14J2iOO21q7Ify7BfgZcCKwWUTmA4R/tzRJ+01r7fHW2uPpye1JNfYBwHyVRA1d6lKXXpc0beAWkR4R6YuugfOAR4ErgEvCaJcAv2if21Q0UTYUf9vWKRJOmjKfdeq1rhP/3FlpWnkSzJLlx9c0kZHbWBZtM8UyHb5PfJnKq1ZMS/l8Ml3HsvEG5WuzAjt7jS69spT1nZPdo77L1OJGI3RKfaVLHdGeiErmAj+TwJudA3zPWnuNiNwL/EhEPg6sB97bWXbpj5reTGMb4zYVbdv6XhVlN1UQTsWVZF4kOP1p98dONJipSqTffaqe/F4tfGw9yyb+qozwLu2rVD8HKzQGsQYfUOJgQwW7UgprTHC0Xve77jFNG7ittc8BR2WEbwfOmVamkr6xmY+n9dmnYq6WQR27eZUpKtSaZdNB5GnsNe2IXvbdkZkPosm2q5Dc10ia9enEGBARHNFYUfj4YAVEgfUBML6P0hpjTOs8u9QR7SNb3l9uSogWmkax2dcZedWbf3e5hy69tsmmABpCmx+l4jClFMp4KCVoG3LVpoIRBaLwjY+xNkjTHTN7TK8T4Gb6YpJO8utSl14HFAE0gBKFEomB3BiD5yhU1dLn9oL1GbETKAu+tTiuS7VaDcUk0l1X7SHtm8DdhPu1GXFqurlMTVrqvk1Z8X1SEFwva2/Iop3stpUcnoS4Q6Kj1oLj16y1sdhFkkeI2Zrtuk3WLSV/T5aRrtPU3qGFWKhpgk4y3oOJr+6IO8l89S7VU/obNogqAjwNL23YzwJgFgFRIVctGi0KLWAEfGNxrGLejDmcsexYzj3qdA6ZuxSU5amNa/nBfddy6+P3sdtO4ojC1wJ+ew+QXWpN+yZwh5Qpw83aHbi3uelEJkneoEHCPF2uO2EVojD4SiF+YHXhOBrx/KA0EbQF3zcYwAtWnYgNNnsGgy15TFt7+XyrGu8t4It9PbZtHpsoNLpo3CGbrbjuwvTeIGkYTkF7O8oJ+75COwpXKXTIUFhHoZWD9oVVS5bz9mPP5rxDTmLl3APJOTXT3qMWHsabDz+Lf7/jZ3zpF99gQkbxjV8rKWJeuvLuKdM+DdyveRLB1wFQOyEW+b6HcSy6Cq6BsvGQnIPyDXntYC34+Diui1/1sRH2RVx5hJb77WDocmMvByXBMWmaZ0P2SEKxhxKFCidU182hlSIvebRR4Co8r8xAqcSJy47jvSddwBsOPJoBpwcRhVWSLpTeQg+/e/q7qIyN8qWb/p3i5CQT1u+aBu4hdYH7VSWL+IKyNuCm0czLz+S85SfzhiOPZ3bfADvHR3lg7ePcvuZBntr4PBVlEDRiQGnBGFM/EJOALXuwKngVyCb+jSh7322XpkrNgVIQUThKoZVGAwXXRedcQJHXLmINSilmlGZy5vIT+a3jz+HI+QfR4xawKIyjsOHqsC5nC8oK6Dwfe+N7uW3tw1z3zF0obNxvuzQ96gL3q0zWGkQErTSH9C3lL37rDzn30JMpKRcxhqo1vP+oN7NxeAtXPHEXl935S57e/Bye+PihqZW1Ft/38a3BYGKTq/2PGsUigei16zZ+b1LEXQuCEgdHKfKOS85xcJSDqx2U66KtIm8Us/oHOfvIU7jw6LM4dO6BODqPsRZfBV9HA8rYeqYBCERhPkq7DBZn8rnzLubBl55m2/hOPM/D9/2M2nWpE5J9YdaThX2W3z22FpBU3DVscgmFckmRQDMZd4PnvYzCmyonLVipl3E3lNNC3t7O6DyMp0TIizBQ7OfbF/8F5yw7EcfVCDbcrBA4O7cGlO+xs7qbKx+/nUvv/CWPvvQM+B4i4FmPqrUY3+D7Pp71Ah1e6PkwGlNNv3dGcO1Un6n1ETGdxM8G6YaK2EYbhFrvSJXbcQ1f22Rt0Hci+/iaUCQwxdNao7XCVS4FlUc5mrybo+C65LSL0i7KaBb3zebcY07nLUedwbL++ThagzVYsVirUEj8uYwi0NkkRTLYIL4PiDBpyvzZz77GP9/2Qzxbwat6WGMR0eFGnVe0lbA2LHNfFS/+fD1262RmpfYrjjuyIH1Zd17F1h0ZwJC07pDwn0gL1wDgYV5ZzR5ajIgFF4XSeX7vjPdwzgFH4TgahYr7kABiLSgwaIacmXz4mLfy5oNP4qZn7+W791zDQ5uexrVVnIrBV+A7Pr7xqXoVPLFE/wUTTVh2WIBNTzTJ+ifeuy5uG0oYKLSgLAVjMwVrWi28jw2wV5mstRkKPhWAJoBYREChyeUcctrBVZpCLk/eLdGfK5JTCqMVynFY0juP8w47mXMOPYV5g3NwtYuOO6QKvlyde85QpZyqgyAYqxAFxhpcp8BHTv8trnv0dp7e/UIAnGWDZ2zXe+8Uab8C7leDGmAk09RFaur5VrN2CvgU4OBxxsrT+L0T34tShbjULIxUSmFtsH14Xv9c3nvUeZxz6Clc8+it/Mc91/DEtvXkxULVw7eWUe3gGIPve4HS0xqs6pyT3pPpMSttZ3DbGCtrou5Cdz0lLTREJF4QCsHWc8fRFJ0ihVyegpOjJ18g77j0uHms41KwLgcOzuesI07i1BXHMad/CMcKjgQK8ek0uLUWg0UrhUIj1rJs9gI+fsY7+V/XfJsx30fZCibvYLzqXmyN1z51gbsVZXLL0oDNNhSr1GnSWpksEoCwiDC3bw5/8sYPMaNnBr4rKOtjrWrgoIwxtUFpAyhT4jK3NMRFx53PuStP4pon7+Qn917PUzs3UBWfWaZAxatSqVapeBU84+H5Hn5Kq1+3kmjZHo28bma6zHbrIPsMLvyVX0Lvf5T8fhH3rRQ4KoerHAqOSzFXoJQr0FvooeTkKbkBiDuiWDA0nzesOoEzDjyaWbl+lDiAwqqajc90J0qtJGAYrMVRmoJyee/Jb+Oqh+/gvhcfoZyHShe0p0xd4N4LFHA4KbakBRBGO9BKboFPnvYBTlxwGFZZ8A1KZa8Zk4NTRNBiMcYD66CVw+z+OVx8wts5c+VJ/OLhm7l29S1sGtmKp3N4rkfF8yj7ZSrVKpO2EsjBPa+5dn+a4BtWsDFhx+x72qRMEUj5p1GP1xFFE71SCq01jtIU3QI9uSK9uSK9xR56cwVKboHefC95XGYPzuLUQ47npKWrmFMcRGmHCgHYat+iDPha8MWSmwZ0C4ABrVS4WcegRJhRHOR3zn43z3x/DVscn9yYT7mrqJwS7T/AndRBRkK2vTyA06ZnTfWKDelCZVDiSW1zXxgugnhglcV1FI44nLhkFZec9DZc1w2VSSqz0IiLquOssOAEIK+swhHBojmobz6fOfU9nH/oyfzovhv4zTP3MT45SjnvMeHn8Splxq3H5OQknlSpehV84+NnuofdiwKJ8HNN1bwvtDJuCG/kxOsVya9ZivQpCWWziEKJwlGanOOSz+XpzRfpKfbQly8xo9hLf75ErliihzwLSkOctOpYjjhoFfPcgVpmAvkwT6NCBsMEIr1McVU7ZZ7UMzIq8lOi4OwVx3PW8hP56frbyU1U8Y2lavw6tVF3Y05z2ueBu04x1rDLLiFXnq51TM3com6/ZN1lMu9GWUFiHEmTeOGNKxQRfBGG+ob4/Bs/yMxiLyKqBsoZfTXZgWtOflRtr2G48cE3Bu0oHJNjxaxl/LfzPsI7jjydyx+4ibtfeJyJyhiVQoX+coVJVWC0OkHZVBmdnEBbG8rBg12b1tahQ/gX0tx0s8FVz8VHozHKpBVlybPrzQGtpKwBojJeJxQxBUoEJYJWDoV8gZ5cgWKuQF+xl6FcD329/fSX+uhxC/S6Reb3z+GoAw/liMUr6NMFXHGaqmUUQJP+GNcjY8w19IdEXSH4ulpgoNjPh868kNu+9xgjRR9vchJTncS3JjHmXj/fdKq0zwP3K0rN+kmriaEJcEXcX7Jza20RX6FzPbz/6PM4c/HR6FA0kpRRBtl23mmjNEoE3/cDXxIIeVEcsmAFX5h9AA+vf4KfP/IbHt+6Di8/wYRfJTc+xqRXpegUGa9MUq6UKXuVQAYecbT7MjbuZxuMpku2gXEIANvRDgUnTzGXoydfpK/Qw2BpgKH+QWYV+ujN9zCY72fewByWLzqQVfMOZKDYhyYw2wuyam8x1OxZVh9t138jC1WjNCcsO5zzV5zIz5+4Bd+HqvExXuV18U33lLrAHVE7n8MRSEiKC42ipbNryF5wjUChwGGzDuT3TriQnC7Ez6dqK93M1aYOfR6LBVc0LkLV1Zx48NEcsXQld6xZzZWP3cpLO7fSVxykUplkYmyM3d4EYxMTjFbGmfAqVLwKvgksUfY1xK4TSsXf41WqzCtIkcMnRzsUdI5SrkR/sZf+YomBYi+ze4eY0zeTgWIfPcUe5vQNcdi8ZSyfewAD+d7AxWrYb3wRrICT7sdT6IetOO5mAG7DiUej6HEKXHzG27nruUfZ7Bs84+MbQ9X3ptAqr0/qAncbqrfdTopCEgDeRJGX7LxKKVwnT8np4b+e8i4WDszB6noRwHRlepEM3Boby/+NhHONsWjfYh2HvNvHmw46mcMWruSeNau5/dmH2DS6lUqxh/7JCUaK4wxPjDFSHme0MsGkN4HnebESc1+iqdqW788U9R/HcXCVoidXYCDfx0Cxj5m9gwz1DDJnYIi5fbOYVZzBnIEhDpi1gMVD8+nNFdEIKIUSE1hFWRUopUPz0qiMvUFpm/KGewJVs+uB5yhWzTuYtx91Bt+7/2o841MxHsbYUGTXpWa0DwN3YKkhANYm71pTBo7WuLPs+G2ya8plEz1L79AEFBZfLKDIieCgkFye85Ycx5sPOxVcB5Xk4FvVoQNwSsrHY2milUD+rQKJuGPB5BwWO7OYe8QbOGbpIdy2ZjUPrHuS8cJuxqpldpXHGB7dzWh5nOHyCGOTE4zLJBXj4/tVrPETCsOEriH8o+JnGRTpk23YTpIVs5Pt7ZLxUS2W4GisgK2LlMIdZPcKUxIsm3Otoe5EFK4TbJop5gsM5HsZyPcw1DeTOb0zmTs4k3n9c5jTP8Tc3iEWD81n/uBs+nM9oVxZEs0loVooVHYnjH2S9eh0Mmyn38jivgVwENAWLYLrFnnncW/itmce4hl5iYFKBT/nU570alvo9/Lk8lqgfRi4obYongJXVYejCWDJ+uhJbrmTIloBeIp8YxA38Oon2sFxciztmcNH3vhO+nKlUNbnoxOfYG9yj5GMPcnr2FBHaAQc5XDg4HzmHjOTkw5Yxd3PruapDesY7a2wvbSb3WO72T3Rw/DYCCOVcXZPjjNaGce3Hp5vwARnCRKBA/V63I454uRnmYbJYPz5xOx34pIs7jQiJQqtFDmdozdfoidfZKCnj1l9M5jVM8jCGfNY2D+HBYOzmd8/mwWz5jLUM4Metxh48gs/i63b1ZvedTx1sE7XP4uaiUtq1lHE+mpEOHDuEt50xKlsuu9XqGKFkfEyxnGoJFzAEm4q6kJ3QPs4cE+TmrLc6XgJlJcW8Vqla8gnLNxxAg9+onBzeUpuDxcd8SaOmbccHZoFGCVNtiunqj9VXyEtlqpA4M8bixGhB5cVMxez6LgFrF3yIg+sfZTnd29mV+8oO8d2s724kx3juylNjrB7coyx8jjj5UkqfhUTbeSpx+8utaEkkCXFcKICSyFHNHmdo5AvUCqUmNnTz6zSIHMGZjJ/YDYLB2azdGgRSwYXMG9wDoOlHgq5HGJDc9LUt4jKaTeZ7kk/S+fTrA9miWYKTo63HvMG7nj6QZ41Hn1+BVM1eDZ0mNbltBvotQncaWqleKyTW6efZwSlAbrZfSiacF2Hks5zxOAB/Pbx59KjC6GckdCudXrL1FbUjJNLKjGV0vhYjHYQC0WjOHT+gSyaPZ9nN6/jyRefY9PYDrb17mLr+C62ju1gx+gwu8dGGNYjjFUmmPTLVLwKxg/8gu/jEop9mgTQIuSdHEWdp6/QS19PLwO9/czrn82CviEWzpjHgbMWsWxoIYtmzmWg0Ier3bixbSglsljERiughMvfDvpZJ4xEJ9SM286OLBw0czHnHn4K2+7ZhZerUC35mHHDpKlg0+O0S/s+cE95eTQVOXYH5mQNT9OceV0eNn6uRONqRbFUZMDp4eKTz2dx3xwsglUBcAdI19lgyq5+IwfVNkzAF4vybXCUlDVBNZzQvtbNc8zilRw0exHPbXmRNZvWs2ViJ1vGdrJp9za2jg6zfWQHO8eGGZ4cYbQ8zqRXoeJVsQnuqGMAaHi1rHfdfwdtDGBxx5G61xGRwFufUhRzOfoKvQwU+plZ6meob5D5/bNYPHMeBwzMY+msRSyZtZih3kHyygEMvvhI6MXSWkPkJthayWzJTvpYJ8xDOzcJWYDdrE9YBG0d3nTkKdy55iGMX2FMqlQrZSrVSm1zWBe8Y2oL3CLyHeBtwBZr7eFh2Ezgh8BSYB3wXmvtTgm+yt8DFwDjwEestQ9MvVp7+QNNRQwynezD7YCx4g0Q5eC6LiWnyLFLDuWtq05Ha53aTGYyO7Lv+3VbmK21PAjsCJ8XRTg1yCDMp7Xypu55qEAUFTSKFhXIPaPyRCPAYKGfwxetZNmsRTy/fQPPbd/I5v5tbBrewkulfjaP7mDb7h3sHNvF8OQII5VJKn5ggWKtR7ReV2GbmKhqgalL2FCamg4jMfk1tnDme+1fFMqaJdhla8RHiyanXIpOIBLpKRUZ7Blgbu8Qc0szWTQ0j7kDszhwxnwOnLWIOTNmU8yV0BJNAzpswdoqT1ANvMjeEo20SrsnXLoKlhssGVzAm1adwo9GdjJqy1QnJ5n0KvheFTozTXjdUCcc978D/wR8NxH2ReAGa+1fi8gXw/svAOcDy8PfScDXw79tqcFlaqJfREq1afvKyDLZs6m4mRYjGXln1kFqG1ZE44igtWKW7qG/b4iPnXABA7meetCmBrppJ0FKKSaBp4C/BpTj8BsRNodpS9ZyAbDS8/h9a5lFew6o8TUisLa195f6g3fzKPKFPvoXHsz8oTls3LmVjbu2sm7HRp4f3sTG0ma27+5n68gOdoyPsLs8xnh5gkmvjDEGE00YSgJlZtoWvrEZsyr6mqBoahcbuC5wHZe8ztPjlujNl5hR6md2Tz9Dg7OYMzCb2X1DHDC0gIOGFnLA0HwGC3042o1tbupUjG1EIdPZXDMVSve9tF+dLE67jhMnGOM5cThl5THct+5RRjdXKFcqlKtVfDtK1fe7yskEtQVua+0tIrI0FXwhcFZ4fSlwMwFwXwh81wZf7S4RGRSR+dbajXutxnUk1JxfTPGTNog86Awkmu4Wk1hJl1M5SrkiuVIvbzr4RE5begQ+Nm7s9GBJ31es5TNK8Z9KUYkCf/IT5IUXEBEm+/r4yUc+gnIc/gW4zPM4w/PQurlT43aDK1mPyC1oALgWB8Wc0iBDhQEOGFzI4hkLWLdzA+u2vsiG4S1s2LWFjbu3s3V8F7tGdzM6OcZkZZJytRycyJNs2Kj9RF4fx0uKBIrHsIs4onEdh2I+T2+hh8FCHzNKAwz1zWBB/yxm981kfu8sls1ZxMHzlzKnbyZ5nWv0oxPKrrNAu5P7vUntlJFJ8G4mOjHWIsayuG8WZxxyPJtGduBXq1QqFap+FeNPEByZ3YVumL6Me24CjDcBc8PrhcALiXgvhmENwC0inwA+AcBAfnq1kPgfapxjVrwm7HYy2HbYIbK498h2WMARh3wux0CuyOyBWVxy7PkoyWOktrU9axBFYWPAF7TmUhH8Rx6B73wHfdNNyPr1mJGRIJ7rwle+gvnSl9h2xhl8cGiIS4E3+n6g8Gx4/eag3fQ1ASuhPD7YwoEWy2Cpl75iifkzZrFkYB7rdmxgzdYXmLFjIxtGtrI5t41d4yPsHh9hZGI0UGD6FayShkXN62UIihW0KFztUHRzgT12oY/BnkCWPbNnkNn9Q8zrHWLpjPkcs+xQFgzMJa8dROtgj3go5jLGD1ZGKY66U8XjXn2vVhttWnDZDeANaCy+QE7ynLr8GB547gkqXpnx8iTjlUkqXpmKZ14/naYN7bFy0lprRaZ+pKu19pvAN4Hg6LK6h+nrpP1pmk2OLluIPBoo4+uLbZI2FTfTHjwIVqJxHZeeQrAF+bePPouDe+ehUCjfj7351SVNlDlpLX+sNf9SrcLnPof++c+xmzdj0mBfqcBjjyG/9VvIWWex/ZOf5GPvfS+XinCWMfF7dALQLUE9trsNN2sIYA0OMFTop29eD/MHZzG/b4i5fTNYs2MDL+Z72DC6nW0jBQpujuHyCOOVcSYrVfzIhWy0Qslox/pm37cXx5kK4HirS82Cx3Uc8tqllCvQVyjRWyoxszTIzN5BZhYGmN03g6WzFnDCksM5cN4SSm4Ra4hPTbdiwZpgkWJNA5PRjBlI13FPgLsTvyRZ/aiZ2KQevMEag3UcxBhmFwY45ZBj2Dq+g7HqJKPVMSa8cXxr8Px6HHi9bsqZLnBvjkQgIjIf2BKGbwAWJ+ItCsP2gCTxN722zhjYKsNSxKrE5pDEh09/8+nKWJWgjaC1Q6FQoL9Y5Iihg3n7oafhuhpPgRGNarLchUAJ+X1j+BcRuPVW9GWXYUdHW9reWmvh5puxjsPmc8/lY4ODPG4MBZpr8NN5JeNlgXisACUEI9GxYUTOcZnVO4PBYg9z+mYwu28mT5dmMGt4E89ve4lNhR62jO1ieHQ3I3qMarVCuVrGMx7W+oBKlB8N5nTD7+NC7rTM3lqC470ERzk4jkvedenP99Dvlujv7aW/t5+BUh/9+T4OHlrCGQcfy6oFB9KbL9W+d9hhbcYv+CxT46r3lNvOSt+pVVMUnhUvuAHR4VY0R+GS59QDjuLJdWvYbSYoT44wMVFm0ig8Mx6uQPbodfZ7mi5wXwFcQqA7uwT4RSL80yLyAwKl5PD05dtJEUgogM4AooaDZLOUXzbKLwn0WcrIjHTNlJpJMgbReVzHZbDYxxx3gHce8wbmFgaAwJmPNoH1STp51KFHjOHvHAczPo7z7W9jx8aAeguTLLLWwvXXw913s/nNb+afteZz1SoighfKvduZbU1lUMd1iSwbfMFVeRbPXMDM/hnM7Rvikc399OR76d+9hb6dm9jhFtg8PszoxBijE4pJrxwom6wBY2urqVj0tY+DdUixLiDxfSTc8egqNziAN1dgplukUCjR39dPn1tiRr6X5f2LOfHQYzhyyUpmFWeE54zWQM9aG/uHaSXPbmpi10IcN913bZZfqz0DWVx3Vrz6NhQGe/o56dCjeeG+zXj94+wqVxjxK5hqBc961O0KfR2CeCfmgN8nUETOEpEXgf9FANg/EpGPA+uB94bRf0VgCvgsgTngR6dVqzrMntpXyQS52FoikXGWnDpLWdYQzzbginZyKIS+Qokh3cvJiw7ntKVHkvMF6wTLwOAkaxoGX9SxPWN4SQSeeQb74x/HR5XFpBS8+91w++2wMTUXWgv/5//gv+UtrK9WE5zZFC1NWnDpTUmBtQJW0ef2smr+wcwfnMuTL67hsY3P0ucW2Fjqpbi7xM6R3ezQu9g9Oc54ZYKyV8aLACkWdU2t+Feb0oDjKk1O5yi4gYK6WChSKvZQLJToz/WxrHcObzjseI476BgW9M/EsSpoPx0q6YyJTyXKEnPsibXIdIG7VT/KetbKqiQdHl2nSYuwat5SDpuzDK9aYdfkJCOTY/jlMmO+H2wyej0idkidWJVc1OTRORlxLfCpPa1UTImlevNptYPOmGa2o8A65WSzxO3z16LpcQsM5EssKg3xzqPeyMxcP1aCjRGOtZgmagCRwIf23UAFkDvuqANdrTW+78MHPwjf/CY89BC8733wwgv1GW3cCGvWcO+MGWwvFJhhbWwD3oyyBl0zrX/yvk5WCYSaS4wFrRxmFQc4dfnRLJo9jwfWP8GTm9fR6+TZ7hQpuTm2j+1meHyEkfIok5UyFa8abrLYf9knrTVaa/LKpegWgqPC8kVKboGCLrKsfyFvWHksZ606kdk9M3GdHFpU3C983wtcEWQcJddMEdkK+PYmdQr4rTbdZPWlrLTxvRVmFPo5dulhbN69I5jsx0eolIP9AhUb2HbvbxP93qJ9eOdkQjwSy6Ybkbbdd4sl5Fm6y6aJW4hTkFqVwpiuKIZ6+xnqGeCEgw/n0DnLsATn7IkxaAQPW7PBTQ0+EeFyrZkUge9+N5ZtKqWCci65BP7+76FYhFNOgR/+EH77t1EbN8bgLGvW4N97Lw+8731s9jwGy+W2A3uqistkfePBSHi6iaj4k/lKsAhLhuYz1DeDFXOWcNu6+1nrvEgulyeXy5N3c+QnHIbHx4JDHLzgHMyaYjRq3Ww/Gw3vlNqFmv3CrR/Xv3ybrKxFiQIRlFY42iHvuvS4BUr5Ij35EiXJMbdviHNXnMw5R53KshkL0DiIKMQIVls846N8gzKGqs3mSNPltgL2l5ta2mO3uW7FmTe8t4A2ihULD+SZrS8w5k0wPLqTXRMjjHplvKqP8bya7uV1RvswcCc+ciz7TIXbZHhd5PBhhoIrfpzxsSPtoUlETo0JgUDLLwJWyItDb77AjFyJA/vn847DTqPXzQdn3AJWBGNtnHWzzpstOjeI48DRR0Nvb+3BgQeSX74cZ9euurgm5IBVxoDolLKsAdLUoNAEVLgjECEyHgSgP9fDEYtWsmDWfFave4I7nnmQvJOn6OYpODlyusBweYyxyXHGJyfwTBXj+wTD0YS6vk4GZifKiL1LSoJDeV3HpZDLkXdy9OZc8k6embqXsw49mXec8EYOm3swTuIQaGstxhqMZ7C+TzUhy46omf/zTr5JK2oXpx0n3Ckz0Kz/ZHHfQJ1oMOpTVgt9usQRC5azffdOdozuZtf4GOPVMmW/TFWpwM3C65D2KeDOVoA0xKJ+UDbriIl4kgq1ybu4pBb5JGPZWKutRdOTKzDUM0hPsZ83LT+eA2cuarvgT3foGKABTjoJ7rmnVroxOH/6p2At1c9+Fr1xI/2/+7vkn3oK6e/H933K5TLe0BAsXRrnZ4zBcZwpA/d04icHo4jEtuTxpGQtM5wezlh+LIcsXMYtTz/IXc89jKtzlFSOPp1jqwiOqxmfnKRSKeObyHFV/VbnpoCQ+PflYsCicpUoHEejtKLg5Oh1CrjKQTl5+p1+TjzoSN53+gUcOX85PapQx3n6vh+LQ7Jk2cly0tft6tWOpqrzyMq7law6/bytUp0WjIKAsoGodMns+Ry4fSE7J0fYPrqLXZURhitj+L4JmKjXIe1TwL1/kACCWCGvHfpyRYbyfRw2ZylnHXgMOeNitGSKRZKU7uy/63n8wHUZ/+hH4R//EaUUWmtc18XRmtxXvkKlWKTvppvofeYZ1OAg1WqVcrmM7/tMLl+OOekkLhgfZ7G1uK5LtVrN3JDT9g2nqdSMBqoxBqVUHCYiGK1xrWZ+cRZvP/JMjjlgFTc9fDt3rX0Uk3exeU1xZISd4jKuHCarZap+NQBwU99WzRTQqUo1TsV7iOsi4VmPyglss5WD4+bwHZdeKXHyAYfz26eez3EHHc4stx9lBUPg/Mn3/TrQ7qRfZNHethaZCrW0+c+4b5Y+S2+SDg/hH0TodYscsmAZ20d3sW33TnZN7ma4PEbV87HVMsaazMnjtUxd4J4WBQe19uaLDJb6mV0a5LwDj2Vez2wUyc0qrQdZ8voA36fguowvWICcfjr6rrtwHIdcLkexWCSnFLP/4R/I5/O4/f2USiV27txJuVwGwH/Xu8BaVuRy9JTLdUvPPR3YWcvjLI4qOQij8rXWgRxegvNplFL0UGDFzEUsPvPdHLP8SK556BbuW7OafI9GuTny2mG0rBmrTAZuY6Xe0qKjgSmhuWLWN0hH7aANopWEozQ57eBojatz5I3LqpkH8oEzL+TcI05mKNeHCt32Ggl2A5qqhx8e/5Zso6z36URU0am4pJmYYyrUTuTRyX0zRWUz0I7jAlhBoVgwYy4r5y9j+8gwOyZ2smN8FxMTE3heBcvUVxL7O+2HwG0Tv1djZg2UjEXtUiqWGOzp54i5B3LKAUegUYHrPWOxKiWIaQLY0XW/CH9ULvPHc+bAhz+MXr0aFdpw25CDVkpx/vnn8853vpPFixdzzTXX8OUvf5nqQQfhvf3tzAA+W6nEHC/QaFbYhjodqJ08i4BKKYWW4BxME8l6rVC0OU6Yfwir5izmzvVHcsX9N/H4xmdQolBaI1ozWXEYr5ZRxsf3Aq+Dkc/pLM8FWXWLqCngpdNA4BskVLKCRSuNElCuxhEHjWbhjEVcdNoF/PYxZ7OgNBstLhaDEfCMh+/5mKpXN39Hk1p03W4imu5Zn9MRiyTTRpTuq82UxM1AOitt1n1DWUJ8Er2I4BqHpXMWsWnXNraOb2fr6A7GJsaY9MpMVsthIvZXo6Qp034I3BHZSFP4ypapIC8Og7kCM3r7WdQzi/OWn8hArg8V2uKKErCmzm47ziGhNEwrEH9bhKt8n9s/+EH8f/s35Mkn8T0Pay3lcpnFixfzwQ9+kEWLFrF161YefPBByjNnUv3QhyguWMDny2VmhuUkN+5MVewRUbbOobWpV5b83hiDDTnvmnc7i1UWEUWv08c5y0/myNkHc/3Td/LT+29i7ehmRGlyVqPFYbIyhnLB8/zAaZUI8aGJHb5es/fJjEuwbBIB13Exxsd1XbTS9OcH+O1jz+X9J7+NlfMPIk/gi8QoMF4gx65Wqw0AnVXmdEQjrd4v2ac6nbA74cynAtjJujTrH+3MBYO9p4GyW0RwtctQaZCD5y1hy8g2Ng5vYdfoMLvLo4FC2wRnjoZf7jWP3/sxcL9SlOgGFpRRFPJ5CqUe5hQGOX7+Cg5bdDCOTlsN1A/O9GBNg7a1lvnW8t1ymYtcl3tuvRX7wx8i//EfTNxzD0prnnvuOf70T/+UYqnEcy+8wBPnncfYZZdhly/nbzyP3/U8vIRcO+K293SJnM6jmZy1FdB7nodIYLMeiU+UJOTvxjJvcDbvO/YtnLz8GH5696+5+pHb2GwEqYDjwu6JMVztIl4Vz/gtvQvu0dJZCdZYRAliDdb6KMfFkSLnLD+ez73pQxy3+FC0W0ARHMTsG8NkpYL1fYxv6k0bW9RpKgC7t6nTiX2qsu3pyMI7sUJxRLF4aB4Hjy5j/c5NbBndxfbJESY9j6qZqNOFvNapC9wdkhD4E8lrl/5iL0M9MziwNIezDz6OHpWv28kVWxxmgHP6bxoQ5wI/rFa5CLjroovwLrgAGR3F+9a3yK9dy61aw4wZ7Pqbv8GfO5e81vxv3+cjExP4CaXglGXCKUqm7YQDS4ZlxY3qFP2UUoH4QatYFo4FR+c5qG8hnz7nIs468hT+85YruPXZB9g2uYueksJUPcq+RRSBy9iIq2UvclmewdEOVVsllyugqorjlhzOp970Ps5ddTI9ud5AXCIK43mUq1UmqxUsoWijQw47S3eQ1XadUjN5edLMLh2/kzL3FJRbUSfxk/XpzZU4cOYinp+1lC2jO9k2tovxiUkmK1WMhAd0vA7wuwvcnZK1uNqh5ObpzReZ3zODExYdwoEzFqKtIoINY0yd7+RWYJ3+G10PGcO/+T7Xex5/09cH/f1s/Z//k51hB9bAQms51Fr+oFzm1HIZsTUrioi71Vpn7sSb2mvvnVGQfn/f9zESiB9EwoNyI6Wdq3FNgWPmLmflu/6Qm56+l8tu/QUPvPQE42oC3OAg5qofnALuW5upCG5GzXQP8XNR4dYBocfPcdHJb+MzF3yUZUMLqCI4gDVVJnyPyYlybaI0NhZRpcUW6bI6EWvsiZx6KnlMBdCnC+LNlJJZ9WjODFiUFeb0DnHw3AN4YddLbB7eysjYGKPlCfyqhzFelLLlO+/v1AXudiShPbiA4zj0FEvMLA2wpGc2px58FCWnEIrZA447HsS0B+g0JcMWAhdXq3zI8xCl+J5SrA07cb+1/KEIfqWCqVaR0JFUNBgiUYkfAtsrRa3EJdAo1/StwZucQGsHx3EC7ltrtCWYDB2NEpe3rTyNEw8+nJ/c/2u+f9tVPLvzRRwriLVMGB9BYX0PpRXGD85dRIcnnme1c5sAS7CjsWBdfv9tH+Rz511Cr+5FROGUPTzrU65O4Pk+nm9RSvCrXnj4c6OYLPm3GWWZOb6aYpQ0TcfUL0lZoN1O/p1OB4KxhrybY8nMeSyduYANuzazY2QXuyZGqZoqFeOHTHfzVeJrgbrA3Y6MBR1YFRTdPAOFHhb0zeLkA45gycC8cMkeKFMibjJ7H2RArRRV6ftoB6T1PC5KcSl+eJ/0/pceOJ1ybNPh6ppxRZ1ya8kwYwN7ba01juOADkQoAEqDFc08GeATJ7+b05Yfw/du/DlXPHorG9lFj1VUqh5Vx8GG8n1jBQx1hxfHbhOyBm9awS0WMXDyQUdz8RvexUCuDwuBn4xKBc/zYhl2sHoIkiVXN52IStJtkWVz30pMtbeonUilWT2S9ckC7XZgnea821uoCIhCiTCzt4/Fs+azcNdLbN61jR0To4z7k3imiu/5DXV7rVEXuNuRCnbKFXWewXwvs0szOah/PicfcCgFHHxjkNBfSDMxSCsxSTpu+llE7QZTs+Vnp512up27VZntAD2Z1phAoed5Ho7jxD+RAFeV61A0DsfNOJiV7/ksZx5+Kv9y/Q+4e+1qHNfiVw2+dgJRBSr0D0ONmw45tuw5NVV/LAVyvPPYN7K0by4Yy4RXoTIxER6G3LiBpl27d9K+kby+ncy7nTiiWdx0Psl67SnANRNzZN23E5s0U5pKaCIIQtEtMndwDgtnzOWlgS1sGRtm1+QI5cokRho35LzWwLsL3G1IAFc0vW6BoXw/8/MzOO2AI1lYmh0Y/osNLQ+oG9DNALwZOHcKBGnOJhlvuja/e9Kpp5I2Xe9mE0/kRzyXy+E6gf26TzBBSs6l17icf8gpnHLwEVx2yy/42m9+woZdm9BiKYcgbCpeLEKqFdKsYo0PSjrPsctWoSqWcW+csfIExvMzNzZNF8DTAJ10FZD1PCt9VtmtONesdJ1QK4uhdpPy3iKBwHGbBYVidmmQxYPz2Di4hS1juwLgLk/g+x5eSkz4WhKTQBe425IIFNwcA8VeZvUNsnLuARyzaCUaTUVZxFrwbeAvm+lx2O3Ckvedpp0qvRxpW4ltmnFYsYLSBhtVKsojl8uRcwWUxeKA9dCuZoYzyO+ffRHHHngkf/urb3HzI3fiao3n+wga6yfrFYlM0nW1jcAt4GqHvlIfo9UqYxPj+H4lEL9MYWXTDijTk3DSfLMd0HQKmJ3cp+uaRZ2ISjopo1OuO50/RCqLwLc9PgwU+pjTN4vZfUPM7p/JxpGtDI/tYqw6UTsmr4N32x/pdQrcNvU3upVgYEuwgQaEvJOjz8kxWOplTmGQU5cdyazSAIigCTzEWZXt+L6d2CQZN+tvq+fNQHC6ALw3gDtLqQQ13yURMMWybWNif+Oxe9pEHr7v4xtD1atQ0Yp8oYDrKsTRsTtZm8tzxkHHsOij/53/e+k/858PX0eVSRwcTCgdqQPrzPdMDWgbbOYYnxij6kwGMm1j6jw8TkUU0koEkrWC6gRMm4F7M9FEFjUD3L0FdO04/WZKyvS7xP1Ghb5vAFGCI5pFA7NY2z+ToZEZzOmZEWzKqYzh+R7G7Fm/3pfpdQrcNFoLJbE83JGnHE3BydNT6GFGoY9Vc5Zy5PyDcMKNI9GWG2NbHzPVDJinwnFPhzufCu2NDp4elJECTylFtVqNQVprjecFVhiR6WL0vJkooez7+MbiONVAhOK6qHAgWwULembxPy75HM98bTO3r7mLqudhtQ6AOvluGZs0GgBKKcYmJ9m0YysH5OcgWHxjGuf5Flx2s/bpFAzTAN6JwnAqVil7IsroRBmdFb/ZpJQ1eWXW0QSAjRB7BRwo9DB/5hxm7d7E3MFZbB7ZznB5N17VY9JUpvV++wO9foG7FZmA684rhx6dY6B3kMV9czll2eHMcHviaEmQTgN1O+44Ck9zOck46fitwprFaUZ7kzNPL/cjijYDRbbNlUoF13WpVCoxBx6Bd9rmPEvOW61W8TyPSqUSiE9iAFfktcOAU+Jzb7+Yx/72QbY55cBnjLHUEDdLOdnIPYsVKn6Fe59azbELD0EqwRnUnWxqmqpIIUqTVjI2i5uVZ7Oy06DYSkyRrEcyv3S5U1U4TkcGnm6LdBsl66UdlyVD83n6pbXMKPYzu28mw+O7mZisUPaCY/zCt88sa3+lLnA3IVdpim6OwUIPs3MDHDnrII6YvxxFfcdOu+lsx123EntMFaTbcdntuL+pUrv8ogEViUC2DQ9z14YNXH/SSUyUy+hSiXwux9sffZQTZs+mlHA9G9mctxuo0UQQAXihUKBQKCBYHHE4Yu6BLJ+/lK0vPl4TfUG8kpIMDWVDu2HxRLhx9V28/4y3MUgJbP33ngq145ybtedU4ibLmUoer6QooR3ot6P0WBARLIqh0gAHzJjHi7u3MLtnBtsLOxgZHw+8S9pKuDktkpu9NqgL3BkkIjhKU3Bz9Jd6WdQ3m9MPOppelQ/tgOuBup39biuwbhZ3OmFZ+WXRVAC+k3hJd6Uiwk5j+LexMa5Ys4bn3/Qmqq4LPT1RJlx+9NEccu+9vGvZMn5bKXorwZI24sKhUbGZlI9H90kAz2vFmGdxJUcxV0T51G2CCsom04Ik65SjqrI88sKzPPDUI5xz6CkYz6/75q3apBWAJtspK5923HAWJ5pVTlb5rZ63o3ZceadcdytRSRaoZ90n/b1bQBth+cKlPLZtHf3FXmb09LNjYpSd1Qmq1sN6VWDqfun3ZdpPgVsAnbHsBdq4i2vXSUUCt609uQKzcr0M5Xo5btEhHDy0CCz4YtHUvN5lgXa7v1n16QTwW+U1XW67VX6dcHxRvEh2/fzzz/P/zZrFrStWwJw5cNNN8D/+B0QiFBEqf/7nPHzyyTw8Ywb3Dg/z/4aHKRaLmTs9I5BL1jEtmvF9H89RVK2mUp5kohwYBdrwpKJEbWnz+cNograacSa44p7rOGHFMRQpYJStWyFkKfOyQCodlk7TrF3Tz5vJgTuh5ISRVAYD8XVS99AMoKdDWRPQnuSjEvsmIPDzPlQaYuWMA9iwcwt9Pb0MjvWwa2IX1aqiogh2ye1B2fsatZ2GROQ7IrJFRB5NhP2ZiGwQkYfC3wWJZ38sIs+KyFMi8ua9X2VJ/LLIto3RNFtj0aJw3ByFXJ7eYi8L+2Zz5kFHUdBuMLvTXrbdLDx53yxNu1+UbrrpO0mbpWhtlVcE2ruqVf4/EW4rFODHP4aLLoK3vAXuvRfuvz/43XcfvPWt8L73Id//Pjf4Pl9wXUYSgJauS/oXnSYTnSjj+35wWvxkmR1jw2zbuQ1RIVjW/ejoZwHf89FKcfeaR3j0hafRiVWF53nxe2fVdyrfYirxp5p3+jtBTQcRvUO6XZOAnlzZNOt3nfT9qfSlTt4hGRZZmGjRHLJkOf1uid5CD33FHvpLfRRy+dfkYcKdcNz/DvwT8N1U+FestX+bDBCRVcD7gcOABcD1IrLCWvvKOs2YJokEHaDguAyU+hks9HPSsiM5sGcOxjPgarRnMJItImkHsElq9Sz9PB3WyfOs+2Zp2+XbiqJ41WqVrxSL3HbiidjLLoPf+R2YnGye8PrrsbfdRvlrX+PKj36UeePj/NHGjVPmiGoceSDDfHLLel7atRWrGq1AggQdvVXgxN/CxvEdXHH7tZz4/kPwq8E5nmnAbkhtp2fi1yxtMn6rvFvdp8Mdx8EYw8OFAk87Trz5Z87kJG8Id4f6vh/uXp26gjFdXjNK16/T7x9NQFrrMB0Mlno5fNEKXtq1iRmlfraN7qKoC5R1mSqNbnb3Z2oL3NbaW0RkaYf5XQj8wFpbBtaKyLPAicCd06/iK0ThR807Lv25Ev2SZ/nAQs5cehwKBY7CtxYr2ZxWkEVrjqNWVCP3kF2lRk4jfd0OrNtNCp2CfTOyNjD3W795M78eH8cWi/BP/9QatEOSchm+9jXsu97FI6OjTIqQn+Luzzr/Hr7HnU89yIQtY6sSbIpKm//VHDm2eKkA8z3jIzmXmx65i0fOfhur5ixv8LOdvn41luJTAUmAHYUC26zlX2fO5I5SiS1ODQYGjeGEapX/PjFBbmKCBZVKnW4haxLqhDpVQHZCUZ+z1mJ9ixGL1oq80hy9dBX3rVnNrrER+vM9jBR7KVfKeGa8rr/v7yKTPZFxf1pEPgzcB3zeWruTwKndXYk4L4ZhDSQinwA+AcBAvsMiW3341p2irtMkr6MPKIJ2HFztMFDoYdApceryo1hYnEnFUTgWtIVqkxO6O1kqZtUlHSfNLXXCUSe5lmbxsp53ytV3Qrfv2MGGCy6Ayy6Du+9ujHDkkeC6gbgkQfLQQ9jLL+fOj32Mx9av52jPa0zbhKKlvFKKqucxPjLCXQ/fh8Gg0PjxDpwk2XZdJTyszIIWVMVnh93Nz++8juUXLI09GXrhGZLTpTQATkWePN3n1lq25fP8lzlzeMJ1oVxG/eIXcMstcf/YddhhXPfhD3PdwABL+vv55ubNHBaKpFpRFjBPZSLLSt9OCWqMCVZGTuCVUVnN7NIgR6xYxYvbN9OTL1HKl8i7o4xVJ7HSnEna32i6qtavAwcBRwMbgf831Qystd+01h5vrT2eHrfTVBm/9PMpZhWSWCiKSyGXY9ApctC8ZZy55Gi0o8gTeCQLThz36wAvDeJZYc1kk80Um1lKz6wys+In5ZXRdTJeOk4nE05WvZN5eJ7Hr047Dcpl5M//vLGtjzwSfvYzuPxyOO64+s9gLfrLX4bxcb46d27MSbWSbXvW4ld9lBe+DwZvfJzfPHsfz25eixWFwYSYbYOPGyk9OpFxh0kwCoNQUcI1q3/DM9ueA8njIPjaxjspk++SbqNm9636SzqvVvdZZQOZZa93HH7a08MTSlH45S9Rb3wjXHIJ8o//CP/wD8HfP/xD1DHHwPe/z/Pj4/zxk09y18REXV9Kf5es79WsLdJ9PYuajZGs9vOsT7ANXoiOfD150ZEMDc6mVzmUci5Ft0BeOyHDJmAF+4oeebj3aVrAba3dbK31rbUG+FcCcQjABmBxIuqiMGwvUHtQ7lwhKYmBHOSrROHkc/S6RdxCkfNXnsBAoae2FG8y4JoBXDIs6/l0f+l8k9vJgVjrnrbGiDiVJOcUWRjsSf0AyuUy41E7jYzUc1lHHhkA9oEHwpIl8NOfok48EcdxYjeuMj4O1jIRyiujSSdrIvJ9H1v1AlGGBlEKf7LMptEd/OLWXzPuVbCeQalw12TdltiI25YOfoRnHgbXW3fv4ud334jgIVoCXYeub99Wk/R02jWidn2tk+fjInxmwQK+0tdH39/9HfpDH0Ldey92fLy+T5XL8PTT8KEPwWc/y4PHH8/vLVjAnS+8EABlhmJ2uu/crK6djJ26tjH1YbNKgxy/9BBMzqUoOXryJQpOHkdFAoaUPb/UvvP+QtMSlYjIfGvtxvD2XUBkcXIF8D0R+TsC5eRy4J49ruVep9SSDHC0pqhz9LklDpt3MCcvOpScrTmOSloxQOPsH8Vr1fni0puET+U+2nHoOA7lchnHcahWqzz22GOsfvxxnl2zhkq1Sl9vL0cddhjHHHUU8+fPrwNqJ5RttjpYuNV9dC0SnGAT3sRhAJx4InbJkloGCxeSO/10ck8+GYN0JSGnzhqYyXBrLY4RJO9QwVL0DZ7ncetTD3D/+ifwncDBlPFr5odE+UV1Sr1TFqVjGEdz/WN38e7j38Ty+QdSUC5jykAlaM9mooRowmxHzeyZ03HSdu7p/JN5JJ+VgeddF+fRR5G//EsmRkfj+GmKfch85zvwlrew7d3v5q/+6Z/4xmc+w/z58+tMBptRJ++drGtahp5Om84vadefPA5PRHCscNryo7l+zf1MjI1RdCco5gpMVCpUfQ9rDXY/A+o0tQVuEfk+cBYwS0ReBP4XcJaIHE3Qv9cBvwtgrX1MRH4EPA54wKfsvmxREg5qRzQFJ0evW2B2foB3HnIKPW4BErK0JBfYCQcRXaf/NgOm9HW7+8i3R7Rd/P777+eb//7v3Dt7NsN/8AdUZ88OX1HI/+xnDP3VX/GuJUu4+OKLmTVrFiLBFnQdHnLcjNPrpC5KqXgSUCLBWdsh5+98//uQzzP5N3+DKMWML3+Z0k9/iu3ro1KpUKlUcByHSphnxNElgSezjbFoEWzVZ932zVx59/VM6goojXgGqyOQDj91eGOj1dYUyYiwcdcmrnjwBj4770Bybg5VHcemgDYNmFFYGmizbLtbUdr+O0nJfJL3yfK+PjTEuFKU/uzPGB0dbVh9cfTR8NBD8W00wes//3P8d7yDxz7wAb73ve/xuc99LpbxZx38kFW3Tqxc2qVvFTdpsqi1Bg1DpUHOXXE8//nSBvIqEJcUnEkqfoWq8QmcyLHfcdoRtW15a+1F1tr51lrXWrvIWvtta+3F1tojrLVHWmvfkeC+sdb+pbX2IGvtSmvt1dOtWNBJ47vU3+RlM3l3NlDWqMYZalEUHRfHcThqyUpOmL8CRxy8UJkxVdBuF5YVPtUfEJ/E8pMbbuAPBwa4+jOfYds3vkF15kyYmICJCez4OJMf/CAbvv51vn7hhfzevffy2JNPNq3fVMpPAsbpDzwArov55CdjX9qFQoFSPs+Mn/2MWX/1V8z7+79n/i9+QV+pRLFYjCcN/7/8FygU+NCOHVSr1TjvZjLT4IAbi0ZRmZjgtkfv55ktz2N0AOQKXTvxu05aIvVh8S9L2J3uTEGX+eX9N/PiphfxtZDTTiZnOJ12bDXJt+tT7X5rcjmu7e/HvekmKrfdVt8XReDd74YrroBPfhISFiZKKfxnnkH+4z8wp5/OlSMjDA8PUwktTZJldCou6XScTPV9k7Jw31pEKd5w0DHMmTkbrRQFJ0fOyeFqJ1BoRhjQ8NkzFB6v1q8F7eP7QC1YP3yJ8ATnmKQWZypKyTCtsgqswVFCQTSlXA8zC31cuOo0Sk4vKIXTQhnTrOO06mzJ8Og6+puljMsqM5ItRkvFq66+mr/YtIkXzjwTjj0W/vIv4YQTYPny2u8DH4A778Q/6ywe+OhH+eO/+zvWrlsXi1vS9c9SrLUaMJ7n8eZ8npnPPIN9z3twVqxAKUWxWKRYLNLX28v8n/+CpT//BcsPPIhDVqzE1SFAHHAA1d/6LVaMjXHy6Gjd6ibZXsk6KBG0dqh4VTbu2sTVD93AKFWML1il8cQCKvC6bwkAO/yJEcTW/zohxwdfFJsnd/Lze3/JZHkSpQJrqCSIpWXznQJRs/CsZ63i1oFyGG+3CJtdl+ratXjbt9fHedvb4N//HRYvhn/8R/j4x2Mu1BgD5TL2mWdgaIhtWvPII4/EIq6pTiBZ/T5r7KTHRFafy+qjESMjGLTVDBYGecvhpyIoCuKQz+Vw0LhoJLYLbb+h79X7Nad9HLgjav4S09olCRgx4RFXmnypB9fJce6yYzlkzgFoE8x4VtW42ixga2cp0IormGqHzwKzZ4aH+bvTT2f4934PvvUtOOww+LM/g02bgi3m0e+Xv4RLLoEzzoBNm3j80kv5p8lJyuVy3fbhPfktLhR4Y08PrFqFd8EF5HK5mBs1xnDQQQfx5S99iW9/+9t87Wtf49RTT0VEGD/rLMzhh3OstfQm5K7N2llE8F2NawxmbIxrVt/Bmm0bM79xrYck/5IxNmrAHv9S5ItFjAUDVz54G+u2voAywSn10SaQOPsOgDcrbjos6366YBmlravnvHnwF38BfX1BgOPAF74Aq1YBAcetlIr1F9VqlXXr1nU8AWVNYlOZzNL9oOP3tWAwCJbjDj6CQ4eW4DuBOK/HzeMoHX96SfzXmdL6lfw1p/0EuPcyCaCEnChy2sUVl/n5mbxr1Zn0qkJgdCKCF87iacVTq8E3FQCf7i/yYf3jNWtYd+SRyI03wuc/Dxs2NF9ijY3BXXfBe9+L7e3lpmOPZfXDDzecoTjdnzGGDxnDktFRzJ/8CWMXXcRkT0/sBOrII4/kqKOPZmxsjCuvvJJ71qxh8n3vg7/4Cw6YnOQd27ZltmXalExE8AWM8Xl+64v86qHbGKdKLPJI/9qRtYG1YPJHY15WgfgGhbChMsxVd15H1VbiOjXIjDPepVlf6aQPJfvdVPJI99ckcMumTfCRj8DatUHAjh3o3/993KefJp/Pk8/nKRQKOAk9yNjY2LTAtxUAp0E9S/Ef5Z9lapi8jlYCohRKaWYVBrjgmLPRRsgrF1ccXO3WlOntKLI4eTV+Lej1CdwA1qJFox2Xfslz/vLjOGTOgfgG0Aoxga1wVkcJkjcH5FbcRbO4nYJ7pIQZ3r2bXysFIyPwne9AyK3WUcbHl4cfRn71K0ZyOW4YG4sPOWhWbrv6Qc2iYumuXXzrvvs4eHSU6j/+I2O//CXjH/sYVWv5/g9+wLve/W7e89738kfPPcfTX/9ndv7t37IS+P4jj7BieLhtG0CgfOrRLjvGhvnV6ttZs2MD1vgdScsygS1rhWqywixWBM/3sWK45uHbeOKltYkt14LWukFh1ykgtwpPx2n1bsn76O/sSoUV4+Nw9NGYefPqlKHqkUfQ73kP6oEHKF1yCb133UV/fz/9/f309vaSGxrCvuENyPr16KefZsaMGXG+WeK0TsUbU+33nf5838dUfYw1WCCncpx8yHGsmnsA2reofA7HzaHRTXyYpLle9Sr+moP3/ukdcKoi7bp0FhC0CDnHwcm5LO6dzQUrTkYZAccJTrTxqpjEJpZWgy26T5pqNRt86b+dDMwoPMktPTw2xrY3vhHuvRd1/fWYtGXC8ccH8sovfAF2766Fex5861vYN7+Ze1atYqxaJZ9hGZEuP6tOSYrMsebOnMlfex7/d3ycF+fO5YW/+AvGP/EJtljLc2HbeAsXsnRykvnj43xq82bclJVF1l8nsWw3ExWefmk91z58J57x0I6DHymSgg/QUF8y3gHC3mDTaWyD91drbXiuqEDFY4vazZV3Xs/BC5aSVzmsm6NcmWzaVlnbxZtZluyN7eFJufu8apXzd+1izXHH4b/pTXDppYhILOZxn30W5wMfoDAyQn7GDFzXxdrAE+Lu44/HO+ss3H/7N4rPPMPSpUuBmjleq7KbhaX7WpaVSTI86a0wq8yo78X5S3hIh3ZQRhgo9PLW48/m8RfXMqoqGCEw5/Q94jWShP9Y29B/XvHt8bbuTybtR8AdzoA2up4OBRyWCMGSKVRyveXwU1gxaymibLArzhgqTWTb0awecVY7RJj0fR4rFPhBvqasumjXLg61liGouTRN1iSRZzosHS9ahkcd1/d9Hj3iCEb7+gJfH6ElRkzHHx9451u6FPJ55NOfRoXybABuvZXqww/z1JlnMv7cc+QnJtqCcyecXvQuy4aH+ZfRUdZVq9w+OMh3liyp64Qff+klzty9mwXhrkubSJse3AYQa9EI2nUwCKPlMX59/628MLw5MD/0AS1kdfV2PSV7UDbKGIUI+wURRdVabnz8bt5yylkcu+BQlOjgFHrx6+aIqYJ2Vv32FMSttbxn+3a+NXcuY//tv+H+/OfIxASO48QHURQ9j9zAAPl8Pj5ibrRSYfz3fx+0Rv/TP7Fo0SJWrFgRn2TUrl5p2/Tob7RvoJW9dhTeyr49GTcZpyqC6ytQFpSgjfCGlSfz87k3sPPFR1Cug1vx0ehgJ7QAouhEKfhKkdRvEWqg/Qi494ASs6iIoCTg3CRfZEVpPhcedjoitc02nufFsu2sJZzjOIxVq/xnqcR3enrY4DgYAsP1iK6ZOxcNfHx4mPdPTrKkUmkYvGmxS626jYqpKF3sszqKk+bUjz0WfvrTYJciwCWXoAoFej7zGSiXYxmgrwL/Dn7CN0g7TrvdQE0D+GKleN/u3bzniSdiRZcfWSoYQxUa2iTdHmItojWeq3BEYStlHl33BDevvhOjAk4rkG9lQ3TTOidBNHE/Fdo4upMr7rieQ9+1jF7dg++64S4+r+4dmgFP+r2zNtUk0zTbJNWMU02SawzHj47ym1WrMN/8Js4nPkFOBMcJfK+4rkupVOJtb3sbp556KkaEz05MMPmGN+A++CDO6Cjv+tCHKBaLdYzEnk4q6Tpn2bsnf+nwLIoYq0h0pUQxq9jP209+I3f89DEKVjOug+fGmtpqLeuQjVeJbJsJ5PUB3BACXfChlQ7OKHQlx4ePPJcFxZno8ODZNGin/4oIu3yf/9nXx496ezHj43Dnnch99wWWHYTigE9/Gu+CC/jnAw7ghmqVf922jUWTkw3glAVW0X199esHcHSntY43vIgIesMGzOOP44fALRMTDDz0EMVCAV9ryuUylUolnsxyuRymXG5aVvq+HWgA8QaN6LmqVoP2k5pTqOxP1NgWGoLTvV0Xaww7x4f56R3XsL06AlqCiUd05hK3JU01fgZ5LtzyxH2cf/wbOP2go5Fq8D2safRhnaRmANyKmokamlE6jmMMf7Z2Lff19/NH73kP/tFHY7/6Vbj1VtydO6lWq7z97W/n4s99jgd7e/mfIjwnQu+f/An2Bz/gxGXLOP/88+sAO8kVR2U247Kns+mm2TtlAXr6F+10FglOh8cIZ6w4jsMWHMxj6x5HOYLjaXypycOpQcSrSx1MIK8f4AbAIhI4jHKUYuXgIs4/5FRclcdYgyIweUraSqe57XHf50uDg/zAWtR116G+9jXslVcCwa5BCDvepz6FPfJI1Ac+wFO/8zv8l5kz+cbmzRzgNXJj0d92gBnJ+3zfx6lWUdZCT0+wegDy+Ty5chnnv/5XxopFJk8+mQV/93cMXHUVXrHIRPh+UihgXZeCMRi/0U/xVIC7oYXDFUu0bTodv04W2WTyqh+g4GiFGAWexx1PPsjtax/BKIIljnYC2bNtFEe1pQ6BpCmJZeP4Dq657xYOX3gQxVwfJvxGWaKfTkUi6XjtONusuFkTbJ/vc/zoKOdMTHDHokVM/MM/4D/6KJPPPEMul+PypUu5oaeHW61FDQ+jnnoKc/nlHDJjBp///Ofp6+urE9m1WknsDU48+X511jAZQJ1kBqK2j3Z3KqUwSjGnNIOLTjqPP1n/BArQSqFCFaXdV0CbSFjTWmwje7OBp0uysM/KJxu9xoUXYaSwVetk3LalJKiWR+hUXwW65EKuQL9T4n+d+3F+54gL8A0oF4znMzExEXOLye3XxhjGfZ//PmMGPyqV4HOfQ/7lXyAUgdSVF5JSCqsU+uCD8VavZoW1/PPmzRwQnrGYlm+nr5uJTIwxSLHIWw44gBc3bCB/xBFo36/tViyV0DNn4p19Ngfcfz9zZs3ipZde4oUXXmBiYoJd551H5d//nc/s2MHHNm3CJixEsuqTdd+2zSGua/o6qUzKesfoPZUKxCO5UhED7Ny2mT+97KvcvvFxlA+CwhcDWoPxQ9F01Dek86VvG/BuqoSzPkbBQneQv3r/5zhh1Yl4vkelPBl7TUyLupr9zSqn2X2rb9FMxFI38WvNw48/zjdEeOjwwzFHHBHH1c8/T+lnPyP/1a+ireW044/nD/7gD2JrkggokyunVu+S/JsFvs3iNAPq9H0avJP3juOQy+XI5XL4BGK3HZM7ufifv8CDLz2JqXiMVctU/Ergt11LIKKIu1ANZwLdRu2ukfYER9Mr0LAOl6/Dbp3I7HyvG45ba43xwWqNFs1Rc5dz3kHHI0awLmB8KpVKw0YXqHlCW18sckWphH3ySeSyy7AJEUNTEYLvY9etg69/nac/8xmuLZX42MREoFRLaOZbAXfWM39sjN/dupX/sWAB/ic/if7a12IO1xhDb6XCB4aGePc3vsHg4CC33HILX/ziFxnzPKp/9EcsspZ3b9+OV602Baapgnez+GmAbqZoSuchIijXRSnNZHmUmx6+kyc3rkWMwYrGRJpmY0LlEuEYSw64DmiaYhNBI2LYWtnN1Q/cyooDDqW/1BOfktNKoZZ130rWnXzeWP3WoqykXNhai1SrHHvIIfzf4WHufvBBbrj0UtavX0+5XCY3McHgrl2sOPVU3vSmN3HEEUfgOE4Dd93Ju7XiypN1ygpv1k7NRCjRKifJeUeTp9YaVzv4WjEj38/7TzqfR376LBV8rBJ0qMj0YrdKkuC+beKXKLuhGtME7sydu9JVTgakwVdoBSrnkEPxoaPfxILSjMCvAYKpeDFwR+CXlOcZY/jXYpEJEZxvfxt/+/Y497hTKhUcFlAu1w+mSgX9H/+B//73852hIT6wbRuF1JK6Lh/ay7y11sydnEQ7DuaSS3Cvv57Ks8/Gcvp8Ps+FF17I0NAQTzzxBD//+c+ZKJepvPe92BUrKFUq9JfL4RmqzZfx0wHvVpNRJ+8KwaDXWqMcjTEeO3dt52f33MCwP4kSzTQEI3udfGXRNtiodd2T9/GW9Wdy/IojY+AGWsq6obVYpFORQzp91rPkKiZaCZRKJd58xBGce9hhjI6OMjk5iVKKnp4eent76+qfzKNdfacqKmkG1klK5xmBdTqPpCgnqn8kMhETMG1nH3sqq266gvu3P4M2wSlJvsoA5ynRKytneX0Atyhs1UOKLo6BExYs59zlx+MYwCGwcKh4mT6Gk17Hot1W3i23oENZMyQ61cUXwznnBM56Qj/H0XPz0EOwezd2aAigYWKIqBmgZcU7dvduPv/SS1x78ME8euml6K9+FeeKKyiXy2zevJkPf/jDlEoltm7dyvDcuQx/+tNMfOYzXDA2xoc2baJSLpPL5eKdmOk6TEWJ1k7U00m8ZLmxVYBA2Stzxe3X8vT2F/DFoqy80uOkKYlvQWt2VHdz1T3Xc8iSg+jr6Q9WeC1EQpl5tegLe4PqxCXhAc9RHy6VSvT19cVxotPsp1KXNAA3+9tJmnT8rOcR05P2R5/MO9pN6RlDLvwWc4tDvPeU87nvp4/jaIVyXfxqGVwdWihNh6bZIYUmG4Fa0+sCuMUaHEfwxNCvinzk2AsYzPcFjmaMpVqpMF6txJ02KS6BYNZ+0nG4NpeDn/0MeeKJejEHwEc/Cl/9KvT2guchn/scemysdkahtfB//g/D//qv/GDGDC7ZsSNIm8FtNhMxJJ+JCK4IF23dSq/v88Rhh1H5xjfwP/Up3L/6K/wdO5gIPb1N/MEfMHH++fgHHMDCyUk+v349/b6PhOCSzDe6ng6IdLKUzyorHVZnymXhqfXPcNVDt1ExFdA5jGTbbL8aFFjKWFDCzc/ezzlPP8oZR58Sv0Pkehfqv1070cNUJs128ZOy4eh7R4cFR+EqxYhEYJjFATeb5Pd0okmDc9rndzPxSTRBRvWNJpz4/ZSCqoeb14HzOFGce9wZHHLrD3l08/rAKZkS8ExH+Ct1upSoMo22/y8nvS6AOxL2ayscPXc556w4GS2R/wVDpVLGWB9rsh1HiQgTWrNDKdi6FRkfxyQ76bveFRyQWyoF9x/5COL78Pu/H3cirTX+88/ji7ChhYw3ed1OdBJ11Lft2IHyfXYUi3zzqKMY+9GPSB7V61rLMRMTnPPCCxw5PEy/X3P+n1xeNitrSi3dAeg3fWYBBNE6sPzRml3ju7nizut4cfc2RGms72Mdp1HvGOUjUpNZJ+NMQ4bdjsQGwI0xYIWt1TF+9cBvOGLlocwszgRXUfWqaK3w/XoHY+1Au9WqpaEeLUAz+SwCuEic1kzRGD1PAmAzuXyS2tV1qmKVNBfdTIySrGMybgT8fviuvuPg5lysNSwcnMs7jjuPx67+F/ANrnIRU8EHaseaRQxCsMKrVTMsY8pAHYljOqHW3khe08Adf2ilMBb6nR4uOfF8BvK9KAk62mS5HPjqaLK1PbbfzjA3ikjdfDPccgvmLW8Jyn3xRfLf+x4ql4vlnZ7nga6XzUaKk4iaiQ7Sz9Nh1lrO37kTs2MHb9+8mX+fM4ctjoM1BqU15+7cybHDwxTDZXJy0sniuJtRp2Deaf0bRCSAVhqtFTnHxfOqrF77JLc8fl/QbpGIxKY23EhiVEWg3SCvTMWvVYKswdQKJJJ5WkLwtkF5dz33MPc+tZrzjjgDULiuS8VYRGwmIKfBLKud2lEzIE2XE5WVFkGk/6av23HT6fdqJiZJx2+Wb1Y9m71v9F5JTjs5dqN7pRSe7+FYJzABFM2Fp5zPt2/9IRuHd2J8i68CN79xjSzN+1L8bBpUlyyjXTtwNfyaBu6401ofsZrj5x/KmUsOD8a9DoBzInEQasTFRn+TeajJSfqNYffb3w5f+QqER29prZHRUfQnPoH/rW9hjjySGZ/6FM4TT0Bo91oulzHWUvnsZ9HWMhSWl7RzbiYe6QT8ksDXW63yqRdfjJeOUTkiwVb+pLIpmUenoDEdUGmVtq7+ohAtga9uaxkuj3L5jb9k68QI1tWBCEp0Qx51lDWYWg2wvcyIb/fGuOa+Wzhu2eHM7h/CR6N0o133vk5ZoNppWKf5TSdNq0kqvTkouYqImKdqtYrruogols2cz7mHnsZ37/4lYjxwBOslypsSML+ysvHXJHCnP7YSKHgOHz3ufGaVZuKoIE6lUmmw1Y7+pr3frZyc5IJymR/Mnw8zZsTHdUV2om6lgvtHf4S7ciXFNWuwM2bgeR7Dw8NBJ8rlsAcfzKDv8+GdO+NtuUnuIqpHJ2CXvM6SjSb9QdSDY/YGjU6X5nsC3K3uRQSlBe0otCh863HLo/dw15qHMU7gR0LFfpTbgHPddXacGihM0XSwDfnacuezq7lnzWrOP+ZMRARHO1hj60RTjdXfu5tWWuU9FQ56b5WZFd6Oo07/zco3epYUjWSNK9/34+P+HMdBKaGoc7zjhDfz03uuY9ipIr7G4icrEla605fuMF7dyzYmzAhqoNeFW1flG45btII3LjsGlIMh0JpPhlvQm51YDTXrD8/zOGRyEsda+N//G8dxYn/FpVKJ/v5+Bnyfmc89x5IlS1i2bFmsnBIRJj/2MewBB7BqchKZJmhnxU3eRxr0pLwvlvOldoOm88gC8zRNZTBnvUur+2iHm+tqsLBx2xZ+cuMvGXe9gNNGEGNrvrLTJFL7ZVEKtJN/o+vkb9rk+4zYMlfdfRObdm4lp5yaojWxQSTZDsm/06VW37Ldfbr8Zv2wXVi78vb0l3QNm6WLSjJe0TiItr4nOW7fD07VstaycsHBzO+ZgXEhH7vtsdl9rPUXmMIvTdL4k9aWU6894LaACY6owrPgQ85q3nXoGQyUBpDwZIxoh2TWh8/qKABv27qVedUqHHcc8o531IoMZ/25c+fyJ3/yJ/zjP/4j//AP/8AZZ5wBgJk5E/8Tn6CgFBfv2gXhppfY4oTW8t8sgE6HQaO2P7l7LykKaQbSe2uAdQoK0XU0wSjtgLhU/Umue/AWntryfOC0SQLrHyP14r86fM0E88aIAfDXfsEwCQdq8tdh26RJ4WAc4cEXnuSuJx7EmtDNQmhlElSn0SRuum3bSfqstk+na/V8KnVslXcn7ZiO18xnUNYYbRWWHA/VahXfGoxAX7GXmf0D2Go1tOXOcsaeTc2+R/AQGk5VsgprVbjfO/yJNB6+JIT9sGnR+7uopN4szFobnCEYBVlQCD1ukWOXHIK2glKWSqVKNXR85CcsLLI6R5SvtZY+rfmnzZv51Pz5bP7d36VcKKCvuQY3lGOffPLJnHfeeZTLZW655RYefPhhvJUrKX/oQ6iDDuLzW7Zwwtatsf1sKwVR1t92YVn3rZa9rdJl3e8JtaovhCfFa40Gnt78PL+47XrKGKwXbGm3EMi8RGLXyZG2P5PaPW+InKiTZOxaSypAW5ARQRnLiD/J1Q/exmkrj2f2rNngurEyOmtTzsshK44mxVblpPtgq/hTEbF0YjWyp3Lv5Io1aQ4YvVPaP761gXjUccJVkAFjPawVMJqK8YlVKPEMPwU5SWOn6Sx9eoXXQZu0BW4RWQx8F5hLULVvWmv/XkRmAj8ElgLrgPdaa3dK0Gp/D1wAjAMfsdY+0L7206EmgGZJDDRLUeeYUehBeQZPfEbHRqlmuG1t5sY1qdw4uFrlq57HZ888kw2nnor/5JP4X/0qhW3buPzyy1m9ejWjo6NsWLKETZ/5DONvfjPu4CBf3LyZd27e3KD5Tl83vGELDqhZvE7upxpvKtSMK8y6j7htrTWOUoyXx/jprdeyfmQrRhuUcjCR7V84DoLhJDXuu0GmLYnrVD1oHCfpyDYrre3M0kTE4vqKqmN56KWnufOJe3nzSeegdeA6FYhN8VpybHF+jdx5u3idgnA6v6mAdivLkU4AuZmsOqtOWe+fFjklTRbTIqmoj0Ur3EqlgkahfMPmyS1s3rENcEAaFfedU1bfyNLFdJJV8/4bUScctwd83lr7gIj0AfeLyHXAR4AbrLV/LSJfBL4IfAE4H1ge/k4Cvh7+fVmooYNYasuM8LparTDhVTEC5fIkXrWK73sYv+b0KL38Sl8nZdIrRkb4p40b+fzcubxw9NGMfPe7jG/ezO7HHmNt2AErRx2FmTmTuZ7HxRs38ltbt6Kktn0+Lbpo9U5T4cQ7vW8V3o6r6oQ6zTe52cYq4ZH1T3HDw3fhiY+WwF9y7Ick7tAJjjjdyTNk2XH5qb+1iBkv0PCerZeutWg2OBPTWkbNJD+77zpOOPQ45g7NiY+JS2526ZSDbUXN4k2Fo5+qAnOqtCcK0fQEkQxPpk/mE43X9DNjTGj+a0ELv7jrajaObgdr4m42zTesr3McNE3wbkNtgdtauxHYGF6PiMgTwELgQuCsMNqlwM0EwH0h8F0btOpdIjIoIvPDfPYuZY7EaIBZsBYLjHgTPPniOg6bvxIvOpPO8zEZYJ02B0z+ja611izbuZOf7NrFVbNmsdFxeMjzuPvss+NavG1khMXbtvHbmzbRF3kbTJyckwXgDa9nG8U16bjT4byzyuwE6DsdzJ3WKeKEAi2/YnhshJ/c+Eu2TwyDsog1oBtBu+4vZK5IRWjujL5h4HQgUsmasGxjCdaCpwXxDQ7wyNY13Pvg/bzlrHNxXTfesZhUiDebDJt9g07ipeNPl/POEqW0i5++nmp+ragViCdBO72b0lob6xg8z8O3lgfXPsF3rvkeo3YCwcGaKlY5NclZnQ4letlmNcsQr7WM35okS1yXoCnJuEVkKXAMcDcwNwHGmwhEKRCA+guJZC+GYXXALSKfAD4BwEC+wxpExwsR7Fojoa0y4WsGOzUCW21jsdYw5lf56f3Xc+YRp9JfEQw+gVwrWHL7vodvarLuJICn6oy1gUWKiKCs5R1btwIwoRSj4RFgnu8zs1Ihl1Q+kt1Js0At6/mecNvN8mpWZjPKAplW6dJ1TG5hViLktYPnBKduKwy3PXI3Nz/zYAiSUneikECw0SVxD3FvgMQsLlOSb3dOLTl1m6ijMdiw/p6x/PjRGzjisEM5YMFB5HUOz/HQRjdMxp2sZjqN12keaQBNh7XiwpN5NJOVdyJuSVMzq5t0eVl1B/B80MpH4QEKtItRgjKA72PyhgefW81/v/yrbBzbjWhBFBijGgHaEuTRtsltIt3e73tp6hi4RaQX+CnwWWvt7lTjWpGpnftjrf0m8E0AWdg3vTWZDadFm7GMjTqEBbHCjese4MZ7r+dtK07D4OCpKp4Ey6YcCm0CXyZh3VoCaFZ4zveZEfrZjp+14I5agWsrYO0EuNuFTZXLaZVvuzzS9azdC2hNQbso4KWR7fz8ll9TMV4gCkky1JIYCJLYaNwgJkkULGHf2JsDKItTD/tg/KkTfdEGSM4Tm9bym8fv5+IZC5FiHuVrlDQqp+tybgHOnX63VsDYDkA7kY9HdXm5xSzpsto9d21ggVQGRCnyysHxFb42iClzw0N38nfXX8aaHS8ijsb6wa5mIbD4yJaJZbHfTahNn9vTiRc6BG4RcQlA+zJr7eVh8OZIBCIi84EtYfgGYHEi+aIwbC9QDYzjjpEGbRtFs+Ezi0EYGx3mf/z6mxR6Srxh7jFoz1LRgnJcfM/HkK2kDIqYGpB2CoztALdTbryTtFnxOo0/HWr2btHgEiWIoykg+Mrnl/f+hkc2PRcqIuvFIYGJVL3yMF5KJsUkUnveFLSbyR3bv1Hb8VorIwL0oKgJ8bnqgd/wlkNPYubChWilMaHzqVa6jubZT03P0ErB1yxeligiipMF1sm6tQtvN2G167vNJprorxEQFazkcspBKj6+47N9bCffve0X/OD+qxn2RpC8g1+polSb3bgvI0131LUVx0vQIt8GnrDW/l3i0RXAJeH1JcAvEuEfloBOBobt3pJv29RFBNp1IG4T4UGwNhYpuLw0toM/+slX+cXqXzMuZcT4uFUfVymMq9vO5kkRSvKX9rKWjN/ql5V/J2myrpvFa5V/Oq+2zd9hHdvVP5JrixaUo3h60wtccft1TEglNn9FBBVZBiTl2kkQj67jX+Jehc+V1P/ieFP80XjiShYlVwM1gPJYt30DVz96B161jOu6aO3Esv10+071u+zt75TMJyvvrLpmlZ0Vv11fTY+rdr9k2bGtfF7jaI3jG3xbZphhrn34Bj5x6Z9x6T2/YHRsGJTG+AZRGhGFqXo1fcreIqGhz2T2m6Z9rjl1wnGfBlwMPCIiD4VhfwL8NfAjEfk4sB54b/jsVwSmgM8SmAN+tIMyMii5ZJHmoJ0km/hrQ+S2Fk8sumrBKrbs2safXvN17lj7BB86622s7F0QOMMPjeHjhbgE8u+sTllXZHifVDQ24yjaceKtOOF2f9Pxs+7bcTJRHZtdt0rXiiIuKaIIuB1HM1Et88tbr+eFHZtAhxYkWR03C7ShXiRSp7BsAqzTXqbalkx3vE6Q6AxDG68IBKFiqly1+lbOPuIklsxfhtaqdh5iCoCy2j9Z/6kCelb8ZuKNVjLpTsufjiiu1SSRWX481kLAVrrmM18A31AWj3vXPc4Pb7uKO557gHFbBiXoXA7lCwaDWBs6Y1PY2HlZM3FJVDEa+mdDbGkS3iy/JumbUSdWJbe1yOacjPgW+FS7fNtTluASaqx0kypldRaPwAOBNRgt7PDLfP/xq7ln7YNccsrbuOCosxnI91MOv7nywLMG3zYqKIMi2nMm2VVrDdjJ605AvNP8088is6joOjn5RFv0k2CSPAygUwVas7CIy9Rao3F49PnHufaBG/Eci2NyeFJTSZo0gNcEyYm+LgF4SzoOwene06FmzZgWc0ZilwCpYwldXakWsBrfeqzd/iLXPnoXvzNjIaqgEV+jrRNP+mm/3cHrZIs5OqFO5MFZ4VHarHqk0yXBvlmcZmVk5dEqrgTG9BhAxAlWLeHKysm5KKtQVuGZCR7btp7v3XYVNz1+JyP+KJ5yQRywUI0/kq13o10HK02472bQk+wLrwDt4zsna4OidTSpj5MVP/xANmSDrGd5enQTX77+Mq5/9D4uPv2tnLroMPyCC0qT8zRV6+GrejeuyQ7WjLvtFODS6bLy6ZSDbsd5p/ONOL0dSvFCT0/IsAqLR0fpT20QiU5LyXKO1On7WWtj0HZdFyWKamWC7954BdvGR3EcwRebEntQLwqBOvBGJcLq5nmJYjTlvNvUuBG86/KJVn0Sdr0aB9jQ9yR8ESV4WK6/51bOXnUSBy9YStHNMV71MFpTLpcbwKsZSE9Vxt0sbRpsk89b3Wdx6un8W3HtU6G69hDQCDnHRSEo0bg6B2LxMIwzzsatL3H5/ddz00N3sXFiB74LOA4h2td/1lQ71rVNxvM0NXwHqYXbVFjLfFL3Np4Amifex4F7L1HcCLYG4FpjsYybSW5Z9xCPv/Qs5x12Oheffj4LZ8zDOJqSyjNpqoHdZ8LuNov2pHOm03fCdU/7Hhh3XX48bx4bikW2Fos8NDgYPz9m507mlstctHYt8yYnKTpO7B6gFYfWLjx5oESgnIS7Hr6PO9Y8gqchj8JXJgXc4XUE0DEHnQHsYXAdTVcskpwI6l+qvnwTcf61pbWETEQdgIkFFD6W9bs38+tHb2fx7AUUHJe8m8NYi2iFTRyb1Wry77SvteOop3vfiRIzStNJXTsVvyjHQQjA23VdxNF4gPg+mza/yBUP3sgVq29m4/h2fAGbC05QwrfT7wt7Qh0WmWV91q6+rxPgDlnteIBbjALtC8q3eBo22TG+/8DV3PLUvVx84vm89bizKPUPkPec+IBVL7FNvpl/5ekCeFY+7Tj7dsvorPQPDg7ypVWrGHbdwOR97Vr4/veD/JTiwbe8BZYs4abZs3nHhg187KmnKOXzVCoVXNftiOtuxu07jhNvQhkdH+PSGy5n1JvAYgOrHrHBgcvBy4V/SQE5xOvVurAUNXDoU6Bm3zC9sov7VVTRqG7JKEEcay1oxZiZ5NoHf8ObjzqTgxcsQVuLqlbQjoNvqnuV425FnQDwVLjzqZgEdir+iZR5sdJRaQq5PGINBkvFVti4/SWuuf8WrnzoFjZObMfg4WEQBLHB9g71KvjSi9+wzbeaLru37wN33UdNcDxN41AbSHF4jdOOnFVoKxg8fFeDZ1EGfOXx/MRW/t+N3+fGR+/jolPezIkrj6a/1IuDgxKN51XxjBc6swomA2uyAXPqr9p+0KbjdMpxW2t5YOZMvnzooewaHYU77kD+7M/QIyOY8HR4ay0sW4Z93/sof/jDXL58Odbz+Njzz5OTbD/SndRTRNCORiuN0hoRuPHuW1m94VmsgNKaCqZm9REkiv+KUJNF1q2eEuAdldeBgrItZXLbqTybiQKSIB7FQVCi8I0BV7Fh5yauv/sW5l3wbnpyJfK5PFXfC8/STBWbat+9wcVmKQ9bmeu1u++07HZmgECovQgBWyuc0C1usFJTYHzK1uPFXZu4/q5buObJ21i/eyNVHUz+ogRlHUzkUkARiOBsso+E/2T1GajtIUgyexkU1TWRKXV2FB3kkdEQnUXb0yX+3iBZ2Gflk8elQ4N2TYIv0QeIbiNZow1/hOf/JcNscAioiZ6HYVl/jYCxiLFgDD06z1nLjuaDb3gbR8xfgZIcvhLwK+D5VKseZd8j0o8FVbGZANeJmGEq952KT6wNtvre09vL/z78cOxNNzHx93+Pf911AM19ZixciPrgBzFf/jLv27CBj69bh0p4NGxVzzQprdGOoi/fh7gum3ds4L9++694fOv6WNQhKgBhm5Bpi5JgcESmfTF3neLGI6rjfMkYBDabxUmnCzpKQ1Kh/vDa2n6BusaI+5+E1/HwTkyiB/fO5a8v/iOWL1mJ8jzGymN4VZ9KpVLn7jeLOuW4W8VLP8uKmwzrNK+0ZVWn9RRCMbRSuK6DFhW0oevgKE1OuXjVMht2b+KqB27iqgduYsPYVjwhAHSRGBoarY+S19FziD9css4qsT8gepZ8v6hPxsxgjXkQUmlJ5NHsvoHpTDz74TPYLeOZDbnvc9xTpfRyNgoTUsvcxF+biBNydyLCmF/mmqfv5f5nn+DNh5/Ku08/j4OHFuFKjom8D66mVHUwnk/V+HWWGtAZB93s+VSAuVU+AONK8VeHHcbO0VH0V74C118fTzBNObMNG5BvfQsuvJAfn3IKB+3ezTnbtrWtd/qZSGCPnc/lIK8p+JYr7rmZZzY+D64kBhHBReo7BPe2NoCSAyqRjLRGPxM4pCGajf9pQyKNEpQk91/34tEfQaQG3lFsEWHtjo3c+NCdHDx7MbanSM53MX7NLUCWy4W9Sc1k063k6p1aFHXKcdfdK0XOcdAhALo6UGBrV1FRHk9tfo5fP3gL1973Gzbs3oYpKKoqWM1Eq7FM0MykxDdLgvaUF2gtEjRrq1ZtOIXJ7rUH3GkSabTsSTJTydk3jJs0DTZi2SSjXLb6Ou555iHecdzZnH30aSyeM5+c0VgFVUcQdKYSs5VCM0nT5bbbxRcRfrpgAbtyOdTNN6Nuugkv4fGwFXjbXbvgX/4Fc+yx/HjpUk7bto38FN4lKZ/UKthw8+yLa7nqnhsxeUUkH445nSQ4N2yWqXE2MTUD8qz7ZP1a3IWJSZ/gHZ/8nRKVxGE2Ac1xB7JYI6BsPapYi1/Q/Hr17Zx7xEksO3gFWjlo7cffJNmO9a+1dxR+nZj7tRKVZF23KjdtjZXkzEUptOPgSADeVglohWc8XtqyiSvvvZFrnrqHtTs3YJTFFsCaaniUXZgnNPaFRH+p8WeRO4Va36lNSI3pWlKyX7aN2wGQ1zEwtMz3NQncdeY4SbmWZDRI8j5qRBUlDcBE+wYRy1MTm/nbW3/ANU/ezYeOO5ezVp1EoX8ArXNoz4uVmEnvb+lB2KkVRlZYp2mT98YYthSLGBHkS1/CCx1kRc9EBDt/Phx9NFx9dR0giQjyn/+J/cIX2Lx8Odp1seVyZh2ySCQ4TNl1XRw3R7U8yQ/uvJYtY9ux4iPhVmOrarvKbB1oRyAeZ9gCuBNhU6JoNZYMi4UbyVjEfiyiFVodKy3xREQyniJcwkXfP4xvqmwY28YvH76N31t0AHmniGP8uP80m1Cnyvl2+rwT5WMybqt82lH0rSN3vqIUuXyOXHSsIIaNO17i1/dcx1UP3sr68W0oDSI29CUngRI70Dy2OBRdEv+mVhMN83z4rlkPG+ofxKl/0z3gpNuuFBtpnwXuzleJafGHNIBPzeG+rQGBkURYNPuT2HIdRjXga8EYHzGgsDy65Vn+x6+e58RH7uT9J5/PiQceRqlYQhwXKwoxBqU8vEoFkWDzj0EF8vfMd+2M254O6I+4LutcF9asQW3fjqEG2CKCXbQIfvhDOPxwuOQS+NnP4jyMMWjHwbvnHqorV/JsXx8rJidjQGk1YEUFWn1XO2jXwQGeeGEN1z54C55YBBUsfBIgXaeAjL5TEpAbgNrWh5F81owyHsaA24RsBA42FZjIriEPScWVuM4CiHUoU+Xah27jgmPewPKFB6O1g1YaXxvw/Xg+aaUU3BMLk3b5NuOwk+nbiUWwFlEqdLgVgrajcEXjaAflBO+cE0UFj7XbN3DtXb/h+odvZ93EJoxYfDH4gBhBKY2JNuI4AtZkgl3EvCWZWIttFImE9zHHHn/njHaNXqmB84vCMyie0Dvh4BMcf5vJY58F7pjiZWiNNQ6YHRt3hlpgIjwIDD9IYpDFoB12ukiUEgk7E2uuSLcZsoGB1loEazwmtcdt6x/iyZee5Q0HH8c7TnkTqxYdRI9TxLg5KlLB1YLxq4GfSaOx4mFTDqwiasdxZ12nB01WHhuLRR4eGoIrr8Q89VT9JDB/PvzgB3DKKUHkf/3XoB1/9rOgHa3Fq1bhO99h4iMf4YZZs1ixdWvDsrehXoCVYBty3nFBKSarE/z41qvZVRnB1wrECUQIESCr8GPGikhbWyUll44i1O2UJD0oEiusjgXajYOkwVIkHnwZ4XUJieuTxPQobvxEFFaqbJrYwZUP3Myn5ywmny+S0y5VP9h6rUUFhpIvo6w7qF9zd73pSbqVSC4rT1EKE4rltKNxlA4OFHE1KpfDRWGrHs9ue4Fr7r2ZXz9yGxsmtjFhq8FZo0DMVqto/guQNpKNN07c0gC9NTl44r2icQ5JeGmgGtjbGqOXPHXBkuqTGRS1W9JyqklZQX2SXEsj7fvA3ZYyBlN0kZZDxtc2kKlagg9vbdgRItBJ5BPKJ6OO4NvApEt8i1HCNjPJT566lVuee4h3HnY6v3Xqucwfmk/OKeAZQWkHpX1M2cMXjS/ScL5lK+pEEdlqEoisRmqrigTYH3JI8ItoxgzkDW9AXXllYBERktE61viL1JsFZoGKNmCVQhdyiBJy4nDTcw9w22MPYF0HjAm5MBMPmJoiMmzotGmgZPxNUpqLygynCVuUxTGqYJDHjAEkJ/U6EZxN/pX43hLaGSTKjcPCSL7A9fffwdnHns5xiw+h4DpUjIcxOUylgmCbTpTtTP46FVuk802Ht5NjZ5WVNO9ztCbnBMe25dw84rooa7DWsG7nS1xzz838avVveHH7ZmxB4VkvsdkqyjBqsQA4m4pHElyrjerWRPtcG+sZ/Smd3xSoTlSbzqNVfmlZewva/4E74qzigRTzOcHHjzilaPAYQpmpxIAdbYfFmoSOSQIZmhAe0hB0ALGByEP5wendvjVoDNsru/iPB67lhsfv4d0nnsN5R53BgqF5IBpfCX4BxFMoYxp8UqSVmWlqZ7nR8j6ydFm6FGbOhB07ag9vugn5wAewl14Ks2fj/sM/kPvSl1CFQgzQxhgqxx0X63ObKVujsODIqMAE0All2+PVCj+8+Sp2MYlvLUoUxnoEgkvqFZFJLrxONJIG7ybLT4n/6aT/h/EauWYbgXT8LNGHkkgdiUDiWZ+6vzbmwMP6WhvoTnwfRSBC2Fwe5op7buDQhcsoikMu5+IZH+splG3tUXJvWYFkhUNnIJ2VJlJMi6NxReE6gVjEaDDi8dKOTfz63t9w1epbWT+ymaqqIiWNNdHmGRW4+E1PwlI/fya/cTxZxIyXJBSSGSuDiHsnMXV3BLKSiJIok4TSNZlnMl7TrKT2bi3LDmg/B+4ESEvNK1vwKA3aKWCPlEZRS9kI6MN7E97HQB+ORBPK7HJgfAs+oeWAYlx5PDexlX+5+cdc9/AdXHjqeZxz2CnMKPWjXQclFhPaQkdmX57nxZx3O0623bMs7nxJucxJ27dz91lnIStXYu+4Ix5YWmucW25BPvlJePOb6fvqV3GKRSgW8f3Aprjqefgf/zjFapWzn3uu7kioZFl1y2lXk9Oaonbxsdy4+m4eWfckvgQntgd2uzbB7YS/OnvtyKVrNFDTwB19zsSAaMZ1JykrON2c8WSdTJBC5CSIJ8QjdQXUiVdiFA8mAy2IH7ynryx3PXY/jxx9OscddBhKFDk3h634Ha3IWoF3O8rSVzTLp5UlSnQfeTyM/NIo16Hg5LDWYBzFpp1bufGBm/jFPTexfmwLnvXQAgrB+D7KcbAmnKQyQLQetKWuHkTPUhN+bVNP6r3j+OFFJ/0nji5Nw5pObiFG1XWR1H2nHP4+DNzR2rJu3or7v0gUxyait3nptIwyokjuHX/sBLdeY7+oLdYk4GSVIFrw/fC5EawYhpXHgyPreOrK73DLfXfxzlPO5aRVR9NX6MNoAa1Rng9+MCvYqg/4eAJehkxzutYlAMVqlTmTkwGn9453oO66K/DzIEI+n8dxHIr33Uf+0UfJ9/TE+YyPj2OtpXzCCTB7NjlrOTBjpdDYxELOyaFyObQodg5v46d3/opRW8E6gVjKtxblBKaUcftHAygC7ZALt9H3EOp/EaeU/uR1ozNrq3OizklxRypKo8w2nX8E5NQDfR2TkPGdkkFKYX0fq2DL2E5+edeNHHbgCkpSRKvAf4lC1XlnzBJJdMpdZ1ErBWMnaaM6KKUCl6la4SoH7eRQOSfwqY5hx/gOrrz/Zn51z008tf0FJBeY8hkx4QZ1hejARzYq5bc6If5oLtII65Qp9ggmy5qRQtoJVCpBqmyb7Ju1l0+BrMRWoDa2brBxuiQ81aciUle3ha8k7fvAHSubwpdLcM7BXJoYQElUT3KA8VhLNnZqQkja2iYHXF2nkQBsItGKCbxsxJy6EkAh1iKeYYIqd2x6gsd++hwnP3YUbz3hHI4+6FD6nALkCpStIecZPFXB86pY3wbVMHt3A8ZF69Zxw7x5TLz//ahvfxt54QUKhQK5XI5isUihUKBYLDJz5kzmzZvHzp07efzxx/EdB++DH8TOmsW7HniAnO9nbssOmqnexKuYK1A1VX6z+k5Wb3gSP/K/qQLOOnbZGjRZipuOlMZR29v65/UFt7xvrG6CS5RUv0lQtLSOuWqB2D97PNgTnHTMFKT6ra3FlQhALAROp0zMIFS15bYn7+f8Z5/gpIOOxtWaiutgrB+3bzMR1Z5YlsRtkUGt7LWttbHDsOib57WLdTU67+JYyBvhxfHt3PTQnVxx13U8u/NFqtrHuiqQUool8r9uIbC6CpsxaKL0t40rVldHhJqjpow49RM+GX2o7qXr3z8N2i3A2yb7UyQaS6ZPdIn6iWnqvlT2YeCeJiVEJIFMmvpZNeIw6hKFkWLrkprCEiGw51NReCJJ9DcSuRiwisBsUDmgYNJUKDtVrnzyVlavfZIzDzuBtx5/JgfOX0ax2INyoOLkwBNUVWGr1fjsy/QRamnqFNiHymXevX49P1y2DC65BPnGN2B0NPbY5zgO5557Lh/60IdYsGABa9eu5Xf+4A8Y6euj/L73cdDGjZwzPFxnA55VD611cEBCIUfOGNaNbOMn99+IiRWNUpNnK6jfEZkYGHWgTeMASFMDWHcAZBHQpjnpOmCGJGddJ6+OKieEEzk13K6xXglQkLq86kQvFqwStnvjXH3PzaxaeBD9xX6Uo1FejeNuRXsyyU9HTh6JRKINVoVCAascepSD+B7bq7u5YvXdXHnntTyx/UVGtQfKJ2dVbImbFntlypfrvkXtUhLP60A7cyK32WV0XGYGaDdNmwDvpH4kmWUd/khjvolHzei1B9yQGCOJJUowxQfgGkWLxlYIvDZyJxaBdRSB0H8JCeVlPO6CPOOFQViub+JRjIQbeDZUdvCf913Lb555iAuPOIMLjjyVufMX4OZyKKVROY0vmnGvgojg+37mLrp2CsIG8n0+vG4drgj/9sUv4r/tbdhLL0X+4z9wcjmMMZx99tksWrSI5194gX998kme+2//jZF3vpNZzz3Hp+6/n1kzZtQBSFZZka9t13HxteXqe27iye0vgFhE6ZpMO3bTSj1wp59L2sFUspOnRBWZMsos+XBy67ok/q3l2pwSAzGpE1FEqF7re3Vy7TB13OGiUsNn4fv6juWmJ+7jzSecwcnLj0U7GkKPjEkLpL1tHtjKDjstSomA2nEC6CgUCrHozdGKHWO7uP2x+/jZHdfyyMY1lN0qGEPeV3haUVVBg9U7DasrOPybvE6GxRGJOfW2oJwCzobnqbCGflT728j0keDM0xOMJBnt+gmhA96iFe2zTqbietUpFWuccPDeJhBVhMDb6AQolYcNr+vyqIVZE14bW3NKFT4TUwuP48W/CLwtEj3zfURUIAv3w2WytVhjUcZSNJqV85fw1uPO4bTDjmPRjNmI0lStxfo+1WoV3/frfkk553SsT6zr8uMDDuDSpUuDg2o3bKDwxBP0XHYZM2fOpKenh62/9VtsWrECb2CAhc89x+/deCPHLlzYcDZi3fcLl8u5XI5SqUTBzfP09vX80Tf/kucntwMWL9j6Vg++qvZtJd7yThyntgy2qYFcV3gtqIHzTq2rEiOoTsmW4IJjzE23Zbov1T2jtkKj1r+CvgR1numiv6Y+XqRW8Y3PWw48gf/5gT+ktzhAtVJmcnKSSqVS51Kh/j33EAWaUDLfpNIxcs2by+XiZyMjI9y55n6uvPdm7n/xKSalCr6PL4m+H8rB42aTkLlpBriJuLEtdSpqg0w7zS1Ht01OSWq4VzWAhsTEIFIflmojGzEhcX42vqwD9aw62Caikssex24ay/y4+xnHHXFQ0awXfsnw1Wz0PKWxkgR3E3yI6AMklspJji36CNHAi0QgUVqhBvAReMeZh+HRiTFKBfONMYhRQc3FMqYND2x5jrW/3MhNq+/gHaedxykrj2FmoR/fddGisZ7HJOUQx7I58FYccFDdGuekPI/3rVvHAcPDfH/RIl6YPZvJWbPYdsEFRO6jnJERCsApl1/Ou1yXg5YswQ8tYbKsXqxSuErhaIXOKcSBil/m53ffwAsT27HKYkTXD56Ys458b0ed29YObJVEeLLdU5x1gx4jTgyNAzRR91g0Uh8h6CmhtXWyTZODsqGtI+vsqD9JLSy5XE7oXxq5vVBbo+Cu5x/jzjWP8OZVp0J4oHLOc/CxgTjU1IN3u2/fjLIsRKLw2KxNgt2KWmt0LjjkOJ9zcZ0cturhmUnuWf84P77jau5b/wTDk+NYJ+HVMeKuw7YTSLRJqtwMbrupGCcLoGkMq/WPJAOYekaSaw7yqOtPKcBOMwm1uMnJIfEsXc0W36WuPZrG2u+AO6TkwCUBwsFFA9koXizwzogrqYsoWrQkjswCozTJv4aAe0yeNSoEozAC91AEYIWQYweUZpgyd73wBI//cC2nHHQEbz/tHE5cdjiqVMQ4DjmtyHuGSb9Sd5hDBKTpAdxuB5ytVjlh82ZO2rWLDRs38lC1yrMnnIDnebiuy8F33cXhjsOiOXOwTXxm1A14G+2KcygWetBWeHzTGm548HaqrkV8i9Ia30QbgVLtE4N58FcSHd7GdrwZoC0JN1BZnDi1AdmabEOfid834pyiblOTwYVzd3IoJ3UnQZx4AqjlnABtW5eflbCPWcNub5yf334dJx14OAOlAYw2eK5F+VWM33pA173ZFFbTyVVcUuGotUac4HzHnlyBnA645hFvnEdefJqf3Ho19zzzEGNmAk8RgHYWh5kep8l5My1iSEySNr6VWuoUOEZx6yhDbJE14cf9KCq3VZ5ZVCe6S75DOl6T9E3wqh3tn8DdkiQxHmqNWuPQbX2cBjFo/YCKd1YSAi4kTAUTAvMQ2OPZO1wFBgmD+NaEPntVjVP3leArw3ZvjOuevYf7NzzOGw87hXeccDaHzjsQt1iirA05r6b8S/ps7sSGNx1HKYUpl5k7OMgFWmOffz6eCGT+/DqvgTHgJzj75AB3Qz/abqEH8RQ+Pj+6/Vq2VkcRTeBIykSHJBBPYDFKR508YRJoE4OqbtAlB3XcvNJ8UKQnsexIGbvwAof8Nim3jh+FDEDUv0KZdQ2ikwO5ZkNcV4O4byb6mgUlDr4N3AWvfv4JfvP4Pbz1qLNwnRxlU0W7AbhXExNpK3CeqgglebxcZIedy+XI5fI4SuMIjPoTPP7CWq6681puf+oBNldGQAtaEexvIKPN6kBUaiKyRLw6X9YZ3zkG76xNOWTcJyeGVJTahFCbXBqOD2s5ESQmlhRf0fA10pNBC6qtctqDd1vgFpHFwHeBuQT5fdNa+/ci8mfA7wBbw6h/Yq39VZjmj4GPE6j4/tBae21nVd8LlPxwSY6oTlaeIGWpbcRJLGWjpCrVigkLksBDmal5r4t6nrWIiQDBJvJLAHr4U34AhDrnUKlW2Vwe5kf3/Jq7n1rN+cefxXnHnM6SWfNxQyWi53loralWq7Ec3Fpb29pOjfNuNrh934+5qWScrA0VWc+jZ4HcU3DzwcB2Hc1ta1Zz23MPBo6SRGMEtNLEy0iRmigqAciRLDB27Rp+KwnT1HNabQZZs2fpPhArChsS1ZdXtzIL+ouN09eDd/2COgnaqQzrwDsELuvHNsyjdpIf33E1Jxx6NHPzM3HdAtarItrg2/oJtBl1ynGnTTkjGbbruuTzecAwUZng+eFNXH7br/nNI/ewaXIHKqdwBKwVfB20R933S75yuzASimgan9dAPQNAE+8B1IvX0mWm4ibBtzFNY+eolZFgJpITUMR8tJq86jKEpAvheIt+1h6ABHXCcXvA5621D4hIH3C/iFwXPvuKtfZvUy+2Cng/cBiwALheRFZYa31eUUqvfzOC6xozHGTpwS0kdk+SAHkad1eGvpfj8RKN23AKlQi4E1y+dS1iHfyqj3LzGN/HFCzPjm/mX2/+KbesvpN3nvwmzjrsFObOnUtkPxsBbwTekQw8a7NOmvuOOKssy4GY805w2kl5Z3QfDXTtaNxcjpxSTFRH+f4dV7G9ugsHjW/A5jQ+iTaNf2H5UUdPum4l+SwxALI6f9ZSNf5w9eFJvG6ZNikaqQP3pNgkVVZduycAPInldRVJMAfRvXiIdqFqEcfl0S3r+NX9N/M7p7+HglWgC/haqJoKaSuTViusVqRC/zORsjF2w+sER4b5vs/6rS/yy/tv4pf338KW8k4kp8ARPBNsEgIQQ+BHOw18DfNWYlyl69v2OyfFLNmgnc47+1pqzqqi8A7arG5iyADtuoKkdtkxSWrV0YLaAre1diOwMbweEZEngIUtklwI/MBaWwbWisizwInAnZ3UfY9JoP4DQx2S1okvqHUuG8ZLHo0WRU6arxnCXXKpZa+lJue2gERyExvna6MldiQrt4KNOPOcDs4kFMG3AhoqYnlk14s8d/33ufHxe3jvyedx4sFHUij1oQsFpFolpzR+tcIklqqAMbXt82mFU/Jv+rrV1uooXsTVR8CtlEI5OfJOASMetzx1Hw+tfwIcBz+08Il1EElRSTwA/PpNFiJ1gJ308thyUIdRUrXOBjBbm4DqkyZcEUVdIvp+zcozSWBPzwq18mr4UOuH8Uae0ATVCljlIDY4yFoA6wi/uucm3rzqFBbOWohyNcbXaKM7OrQ5qE4joEffDyXgCgXlkNcubi6PuDmUKFzj8cK2F7niwd9w9erbeGl4K1V8rEO8azgpcrDWZnO6KjXTZSgmbTJNGvAyQLoRLJulTYltUpNKW0dV6fLjP1G9E+MrWq0nDUSk4YL6CMEjm44SyG6aVC6gKcm4RWQpcAxwN3Aa8GkR+TBwHwFXvpMA1O9KJHuR1kC/V6gVl2GTF1mNmanlT+cQfTWbcIoUgXIA2MEqOsF9GQuhlABrA8FRUNlaWPzlbE0sE8rEA3/VMGrL3P7Cozz20hpOXXk87znlPI5auJxCoUC5oPBcwalopOo1NR9MKjKTopCs9svapZe+j0zDcvk8rrVsnRjmR7f/mnHxCQ6goOaHuY57TgyCBn/btb8NdrGk7iMQiuqXnLDjr5b6rhmrrRqYJr4bGYMpKQEheR0xAI3ij+wMqO+HcZqwNmFeESCu37mZn919PZ98y0UUtMOYDlY6nuc1fKf0ygkax0W0UnKc4CzHguPguxrJuWjHRYxh8+4t/Gr17fzq/ptZv/0lfDyMSogHovaL5qr0t2r4bqSe2VqLNIBtomHSz1oAeB34Y+vFLnXgK3VN37re9YDdIAdPVSWTc0+Jg7JXE6m/UboW5XUM3CLSC/wU+Ky1dreIfB34EsH7fwn4f8DHppDfJ4BPADCQ7zTZnlESVNMDJwneQrgRJxEe3cfccoLjNhKbmGemS5cXgb2FwL0OwUnxcXh0rFe4AsBglGGn43H1Y7fx0DOPcM7hJ3P+KeewctFSesXF5vNUdAXfDyxPqtVqbIESvHqCO2gDymlKy7mjwe+6LlopcOCmR+9m9ba1+PE5gJIJ2vXbiBPfJSk2aQvatb82uqhtkW1OyQEcvRv1dh+Zieq46uRKqy6jzPzjVZ5EHFrUH+LKJxKHbRB7u7VUHcsvVt/KG486mVVzl5HP5bGG2DkZ0FK/ERQldTsdY7GI42C0Q0k7KAWbd27lNw/dyRUP3swTW56nWgCrA51KbDEV1T1rAmsA3/rmqM1z9UwCpBjMdH5pSvaPJKgnyrdJbjtVL5uOn847fV0H/KnysiaVjleFqXdplz5BHQG3iLgEoH2ZtfZyAGvt5sTzfwWuCm83AIsTyReFYXVkrf0m8E0AWdjXGjn2kOo6cnoGbOCOwg+uapd14o04DjXRSfJEHZWMb+OBGISFgzX5k4jLiuIl0CsEckGjfYHJKuJoNjDCZY9cz21rVvPOY8/kLce+gVmDcwIg1apOBh5t2kiaD0Yy7ukotyJ5aPTLOw7P7t7Ij++7gYryEeVgbMqKJGz3Brl11OSJnZKNGypaDNC656nwlu9Wj7i2djxLugHqy4jS1sm9ow4itTRJrrHueZIrb1EvFba9Bathe2WY7932K774nk/QQz5u+7QOor7qNgZsrXVtoo247fDkGY1lx+6t/OaJ+/jxPdfxzMgmJqsTuK76/9v71mDLjuq8b+1z7p0ZJFlvyFgiSICKZ/QwIIEFsa3YsoyTGBycmEoR4lKVkip+OJWnSarspCr8cFUKhTguV5TIRnYZA8YiqBRskKUxWARJSDCMRo+BkRDRCwk90UijmXvOXvmxu3uvXr16n33OPfeec+/tb+rO2bt3P1a/vl69undvrNaENVSN7lEJgk3qxMhT8JPO7iI5s3HpMlbFZJF7FE60sS6tWspGhlZttUcxzrYy+Ho38mnMejy4w18X+uwqIQDXAriPmT8u3Pc6+zcAvB/AQXd9A4BPEdHH0SxOngfgjt4STQMO/02E7ErBRZdTon1n1SoXBTUNM5xVwe2+be9d7v+uhQS+jdV+C1Xjr7G+UNvfGWD3YYJ69woARlXXoHqEh156HL9z6/W46Z478Q8vuRw/df7FOOkVJ4XDf4bDYVi8XPN7wB2J53acTNpe5glgdXUVw+EQVNe44et/icMvPoFVAGsMYJCSaZi6KvIm4S9aiddam6UJyevIRKHCh8wlFyIOSsk+MrMITda7+y1CEU/L9gMxIAsNMBFIkEFwanYXDBlgqvFXh/fjsu8exOVvuASjijEcDlGPa4wwCrMgafcO54gMh1gZDjH056MPhhgMm5P5Xjh6BF+5/w7872/cjANPPIA1PoYhA8NqgHHVfDSkRoUK7v2DiKxkWel8STKOj1M1TUmEyL+qBNMpp9W3HQsx6fbSanWcGcKX7VEPLtaAEqJIiT2UxpRadx+N+1IAHwJwNxHtd27/HsAHiehCl+5DAP4ZADDzPUT0WQD3otmR8pGN21Hi1db+aIujVqMdkCwIhE6IuK3JDgoI84kXq4mH/N5ubtzCq7/eJAKAB41m5Qmb/bYTYVLhijD22y5qxriqMK6GADPGAA4++30cvumT+D8Hb8Uvv+tncekbL8LJgxNQ0wrI20OrCoPBEKPRGPV4zfwCj0Xi0lY6REMEu1eGoNVGizvw2CF88cCtGBGBV1aBUd3sgW7n+w0JhYbekJp/HZ1lpZAvTFH+JAo20mxEfO0IIKWPfkJ4OXOqVdsRhJx0my7bZNCk/VRLDQLu+5tcc/osAreE6ExlNQE8ZvyIXsZn/voLeNtrXo9dwxMxWF3FnuM1jq2sgY/XqNz2VCLCAG7Hz8oKhqtDrAwGWBkMMKDdqCrG00efwVcP3YkbbrsZB57+HtbGI0fKQ6xJUnQ/tSZB/0zmXz5QZqvw1MerT/2LylI5iGTZeBaFEG0ht61wkrbb0oBQMCJvngBUXwkzLlJh2LjyXtS2U0PeHPrsKrnViBoAvtgR5mMAPjYx9XUjHcFmigJQs1rRuSR5+06ntSqJCsHOHY6A9Um4DtycbRIxfbuo6VtctMPF/7IgHgruPACOYYRv/L978Z0fPIR3nPMW/IN3X47zX30e9lSvQDVYwa7hKo4eP9powyMKJhQA0ZuYTdL29JYHjRZfV4RTaYjnRy/hj2/7CzwzOtLsHqBhsxhbOdlChxeNmbzo6o21UB8c+Ys0WgIIat9tphPn3dFyS2T+8pdNQ7ColbzWHZeKajsqIT9Awx84ZHnWo4ugKK6aM0yIcOCxB/HFO/8a77/k51HXwHjPCk46xjjOazhejzComvWS1cEKhoNVrA6Hzbnmu4dYGzCeef5JfP3QfnzhG7fg3h8+iKPVCMGEF8pUtvf4+AFJbuEboXFJOP+yPnMkrVk39ebDJ3URDSRyUKcQxtS0Sb14I+QOWZftRprhwvOcnCFQ62Ctu/jujfTRNNjab07Kgp4+aNNFpPajO11ikxSdjqhdiIyeoW3v7M+vcH+1f7WZY9KQhxDJzqPJ27vXIgfc2GhrABgAz/JLuPl7d+Gu792Dy86/BL9y8RV43d7XoAJw4q7dGI3GWBuOw+Kl34Eitw/qtyW9GwbU7PHd0yyQfe07d2HfA9/EaLUCjcaomDFarcD+y9va/ix/IX6FH3Jl2zRsjv3LMLpjWs3A7GUcqtUOlxJSCCYHdC1PGNClvDE5s48/LDqrjk2I2xRVqMc1Bi7+l4aM627/c7zptW/ABaeei2ODAdYGQ6wOBhgffxmrwxWsDIeNbXul+ZDFYEh4/Pmn8LWDd+L6e/fh0MMPYLTSHAkzWBthNFiJ+UbmyaindgtfRnGRA2qWjPu4URSXL9rIr6j71ivZebHuxWVspovjTuNj4dH9eE1bt1eVpaxc2n0CrW1t4l6vtg1tt5SdEIhebwbaSvOtSO4wkc+kiYQg9nZTbPP2ndcPv+Io2EDcXh7/G+zpJBJx4nDz8s+oAp6uj+L6A1/BVw7vx3vf9E584Cd+BnvP2IvRnt0YHqdgA/fnn/gdKPIMcLkjxe9EGK4MsUpDPHj0CVz3tRvxMq2BiTDYNcTa8RGoGiJSiUNjdnkUBB6IzP9QWxRR56TUXy+boNU8/LG9Hppoo3vEHnOzMXktw+baj3f37UhOvlzbcEMouBpgPAB43Ji7Hjv2NH7ny5/Cv7ziQ3jdKWc3PZgJJ+1pvl5UDQeglSEwOoYHn3oMX777Ntx88DY8/MIPwfUa6tVGhhEB1epqOksQ+QilIsiQo7I2BrFojM3sle7tZgzY2q/T/P2iYqDVhADb+1SDV34tjT1qE2TGa+ZnUr5yckwwl2yxY12hSn124o5ehgjxilr1juFeEKl/Hm3rk/dSU/batnLz9lWZjowrcmMjzQptr/CB6uabmLKMRmsYrqzi7FecgV94y9/G+y54D8489XRU5L55OR43W8tGY6yNRxjVY4xGY4Br1M4mOxhUWHV7tnft2QPiGp/Y92l86u6bUNcjjAfNZvVBNcCIx2EQJCDejQAg0sRdkQd3AO3xm4LwjSlr+5vp0IYT+/KT5S6LL3gU/rS71SYi/6TqMlPXHuFZ6061M6gwgKqZwVBdY0gEHo1AwyHecMa5+LVLfhFv/fHX4cQ9J2BAAxwfj3BkdAyHH/0+bj58B7714D34wcvPYUwjoK5RV833HJu6d0fptu+1IvqINkINpqapcK+JO/zXThw7STozAAR5qjiuEEzWuRiIc4O5HphMeXqQd7hWLz8R2kIiapdprJe3qGr9WZAy//4B8ONHTI9bmLi9qjA7eccJ+nKOyZkj0vQehVyy48oOXBt+vOYd/Lo0ZSf328Byg0auvrx8NUdZGDBhXI+aozmPj3H2aa/EL59/Ga646FLs3X0KxgyMBgPUa8dR1zXW1ppPqNX1uHn9ngYYDgdYHRKq4SpWVlfxfx+4A7/5F/8Lz43XQIzmI8BE4g3TjKYEtPZF3/F9h8xoG34LYXzkp4wQmKoNJCTNhhtAzMq5rTNrJuSz47fxkXjGerBgJzNDhVMDtJgBBtN/XYMGFbhm7OIK55zxN/A3T34VagaefvkFPPGjp/DDI0/juEUO4Z7aW0rfwEy3xCGuE4jjaicNnl1Vk9OipWMSn3LwH/I242rbTMOt1Mrr+3ASLv6gr3nmiDZr+h8df5QT6hh8MvndVsTdesDGELd0UmQs+lJeE/bXFPsBWjJPyLt146hzyw4v841YruBOkORCADBuOnpdjzGgAapxDQwqvObEV+LvXfAe/PxbfxI//mNnYsSNtjxeWwONavDoOEYYgzEABkMMdjWfpTr0xPfwH790Le5/4ZGm3ddCI/PatOroQHwfVub9zpIO0g6kLtNobQkwO3cHyKmAnJSdQFK24sIapNG2Ha7rUHftBhFO4xOL0BF5e3mSNH32CbV/YxeEwYjBg4EjJacdMLv1FZ0tNurF6P8W+RhkmBCmDh8yq58bbaMvwWu3nMatyVbKZUand3iQHW8SUPgxyy0TVrqb39Yk4NpvZ4l7i9u45wiz/fnzRRwJUy6Aa8C1eixPHWQgfJBYam7sTwzk0DmjKX1IQmhLgvSlCOHX270Z7WvnVYUxN+dJDDDCA0cfx3//+ufx5YO34xf/1k/i8jdditNO/DEMiVDt3oWja4xVDDEYuTNXauDQM9/H1V/5DA499xiGAEbE7svtLm3xIk1bDqlG4284vo0bv8+yNJMknUSWdw/29mMbC/9a65Iew7XMgGsPcscAi3M6/JG/jjjJt5todU0m077m3mpzKm3fKBy5V6jAVQWumy/EVwyAm7UJanREjAZOW5SJGWRr7bBICMtq94rgSJeUC5tXC9twgKHlJ0nqOheDualxWwQtw8T5sU8UNNozXHraDzxfGPGY98mFSjN9JLHFiVuT6fqiYtKlJVQddlTD1E6fvAbtC9u/LRm0KbSKpe+TkUbu79vr5A3PaGbhG4wguMi2qgYGH2zsTBlcgwcVxgwMGABq3HvkEdx/+5/is/f9Fd7/lvfgZ1/3Npx+4mmAe815TGOsrQLffPgg/mDf9Tj44qNgjEE0wHBAWKvHgPwsmUSmM7F0k0VOOoxB2hb6kLZDnkh0fF779SSNQLThKGCoso/ikOmJzu2IvN33y3FdRgt/Kg0waDAIbWg4WAFXNZjrZoepb78R+QuBZDlHhKX8RucgaUqW5UPultLHuiAM9DrFMGdrduGjWYQmbJMsO9pSVjvuks//GO3WuqeMu7yfQNoAtrqpxHBfnyRGGqzu3ccQ9HSZhR8vmjd9uOlwNGX2i1L+bcpA6Bxr7iF+SSZC3mgKXodccEiz3cZShVl8Ba4YxDUIhOGoBmgMVEOcesLpeMdZb8L5rzwXe1Z34cW1Yzjw8Hdw+6P34Uf1S6hHa8DuVYzHIxBVIKb2BQ0g31n8T9SIa9XpkA4AVtzkCmGSVmOgNenKRWk9u3H/yVlMeKbrnePn/oUmHYf2y0bYxDzDaToENAtc7LaVutdtXXuquKGQurL2Pxua4iwDohVUDMjZl1ysaNwsg3Pp6TajblkuZntUUkCrPUrpJJEbbdiMg+Mw5ImboolxFK5r0LDaOwH4n/vBj203G/dmIGMHJdXf2n3VUB1NasDc8VyRudPSuW4nu5zIIwaQ4CY+Nw8ZMJbNk5dZ994PUfPJsfE4aIIkjvLUhNq2Y9URhUaSnnMhOkDyzNCcpK1bgKSfDmTt2olZShOsfIaw8MiyDqOw8QAbBm0df5cMiRyibWhvOTtyX01vEghN3c8Ak13M9NUsQc2ygnYtT7tybSbR3An2GSgybXZxufv2xapKeM0cP0acnM7anFfRUeYy7azZRPirCLhmP/ixF8yC3+KmkgVBFiUDkf0y2CkhKsg3Svern/tH/k1LH504bCjy76fbPu1Jek0kG5I3BiPfooOO63EgbN85Iu1aF0OIRHas5kKOHwn5yntLA7fCyLT7ckquqGSdhTSFhqsCMtAqr9Kvjs94lKQb0lEyyOedwvtnRtyJJmn4MdNMo++r3k3zEQcZf0La7jeNLiX3fPl2pekalO9SauDIfphhUryd6c3PXyHuLkRE2RZoaCjRgqXuZLFzuxGAG6YRU/aI1P3B89oOrr03aoUSyKp0Qz8L+UqJIdIMq2bPabM2q6aViUbTftg1fQsNrawk/kJQ5V+6BzcKGlacabKzbUIPpO7aIs5QRiJ94RAGIhb1F49e+fYhB3oRPK0pJbpvGla+OsrAWigkJ4e1KJguWBrC5ROb8Dz6SeSKylrm1Q9ifcxjHXbxKJ3kmTtPKIrKeImIEqnt+LtkNMNkBlgDhbj7wNJMvHvsIDprTPptR3deO7Req+Za2vC9l4RGZrGeEZcfgLSmL/2aMwZxnTNn+CQmmDX0FDjRti1Nh1T+IiLVfrpgaK/hJEZFCpp0ozIRphBZB/4yqOSanvRgwC2JE7dHA/tUWQ6yBmlFnu1nJJ4lPnRdTIhrEsioF6uqknDoOWuy5O1jFyf9EIBcP5BtNji5wc5qw7l0czJP8i+eZc0zCktM3JqUgP4Ttg2ArnylvjTSKvmkJhf6O4lObfwSxdqp0LhZanchAZFY7x4gZc9oLE2Cyk1pBCQElJpwyhAijO4sWgbjub8Pflu54s9fmTmM5ZCdVdo8fD1JEwiLcg7JchSdPaBDzWaM51Ie79+TeUhVxjFtvTb/WZOxiGDDDyX+2qCUtO3s+dpahA7Z2jC6Ddn+4jz0rHcjr+2NRape0Yo+96DizCRIk+pKt4c0v30ZbsmJW5PUAok7gNAsREiXOlF+2S9Yek0paEw50gZAFNlOWYSV1/EBRcYIIuHP5mAWs/9w0Ya3ijZpoFJWURyecCwCFqLF8bL9hmX0Rp54FhE8tVmNOrcf/Iy8AE3ZuY9ZkCdt/aIKCb+Jdo24zFS45jFp57bufLwWQqcV/rKk04Euzc4tqJkSiGC2hHG85jZCby6S8Vj+LBHNNtRKY51lncTVYUYh9387kDGAypw0J8qDRbikVydrEZa668GSvcvNwBITt4YjzCUEo2N6I0lb/3oi8GTgOLk5+ApCo5ugUnhijrQY979/IcTJGDdl6WIyt+nSTh9ZEaq/trQnSUCWpuOKRsfl/ZNwc+nG9llF3hZER2x4mxC2drEIG82U/G9SCq0/X9pJVRkfXkjMMe0g2nqzCKwHNEmapGS7tYOGNSj1lCXXVE23HmRu+I2SkANrYhqJ25s5OJOR2zbyDm1+hrpJolhfHFuIuJcFPVumJoSg7WVat+cjSSCy8YW3N6nVuqOpPMXKYDRrE4ME0GgLmhz6fDScPOWhJVVN3JD3SlvMkXKIu81Lq8lL0haCmKSkHLPabVMYTQn79L1m7chckrcRNk1cqZpa1qS8FaFX4nraTp0z1+j7xM1qh1Umvh5lu04yaqORphlKCJaFe5KpxA7e1VYys7PcILBuqP6g04qcu23dW4i4rZa3bFAagJ+Oy2eRpi2n47H2mHCGIPaI4LoGAj9ghDYqprI5zS+JI5NNTca5xaAuG3pu4cYPBnpQmBiXLMtMuagFqYgggllEEbEuK++fEIeRyUV1b8Thvz8aqdqNv2lbedRMpO1XI1ufcZqdr5+LMDOjI2g4Ex5qN0fWrqxuLCVB38t6SwUQfgyi7QjaCzn5psQSE7fvYOp+mRG3/lhjNF/yoNYvWj8stXSpQXu7d3QGiiQEIUOkcQOo2e6Qntj1Z7x0fiI32UGER/3MeyHdCZv/CIIkSDz0HGx1YnN6bOz3Za+pGRpzGDRFwtHgxe3PRK1bF3jkMYy0URPQZOPCtzGIeleFaXZ3sVYQB9Mjic5D9unMSLYSGpp52gwnKA1Z0jYGfCu+ZLbgfrXldZKSEEVgzbqMtCc86nTvwNIS95xmXQtDZDP0BBAeKs3b/bYf8VWamtfeEg1cDwqShITHaCqeEbjX8kFGo0lIuX0e8Yd8xkD7mSj/Kwdro7WrxUnvRr6MpH8RZZRlNYhGH9LoMK2Q0NRb/77qlNYsp+BiDEg18kSw+JkhDjsZEleLL1STMx9Y/czkpMkd0tppYu4+MY6S1fEn5RVHmgmu6l7axnWQRGHIxJsTQd1H22BzAdTAkp5IiOA+CUtL3FsdDQ8IIjJf7og7XGv1IEMDFCyvCL+NF4LMocJa9y0BTZWxqAFq7dfwDyAyG/ig/jd85NUgFFJTd2vgkO4KZta8mUKajfQuEqEtNxMbQexhUJKDMouiVfFktTMpKCs5csgxdKpRc+JHRmEQVy6JnDxqoJvqDdZe/jo86nI28seRP52uPdj1hW2KygwoU2qhfbpjIe4NA0f8bM6oowqVhAF7NuYex+6J6tbGAURHO0Qv4Gih+jYuPZ1ky729YHFta+bqWqejw3jS7DPVjzRFPcI512hftyZtagccw2zSfPBY15sibELyYo0prTWAmpxv1ZPVBrSTKk+rfLtgtsVZmM/QOAy7fpa8koFb5yOTTzOiCUpHVgbZaI10Js0I5oCJxE1EuwF8FcAu5/9zzPxbRHQugE8DOB3AXQA+xMzHiWgXgD8E8DYATwP4R8z80Nwk3oJo+7vu3Gjbj7av+geSMMKvjFSGE6TvjTV+sUprcoYGOXWmjLDm9C9p4/KgKrRy6/gSbckm7Vw6sZvMLxBeKkkYgkDEYjuml83QoF3dNFWqCNzXR7KVUMYp3XS95jLUc9AyA4YI7HsvR1fYzvh7eUKsTeTC5s1WWbm6FiSTe9FfZoJFzl2RzY+0gX6WzWMALmPmCwBcCOAKInongN8GcDUzvx7AswCudP6vBPCsc7/a+dvxaBRdp0Z7wjLrUjzw2rHQNFs3as4SqQgYEKiq4D/zhar1Fz5NWZH7E0nI66TReQ/yT6QNtOmJ+KKPXaMhSP/ZJp+O9NP4aP1GBebS86cS+scMtMe4EPKvJduV0MQRZE6JgJXfVh6fTshVNgkianMm68zHoWWOnrf5JSL1F0qg/SOkf7LaBk0badqMbE89C47I/kvAIOr+swjZtI3rckvqA27QFGUjc9NXGfFFGIqT0j/dD6hKy9vHBeVGQFTGIkzOvk3SXwYTiZsbHHG3K+6PAVwG4HPO/ToA73PXv+Tu4Z7/HZrpyLDtic52rzuy5WY03oYMPSEqcpDXwX/uWv7pcFImS472uiHVVqbwlp0kXydz5F/F3TbimLyS8upFKgZkPv29zl9SJ40DizxEcktCJDiiFHmvKI3fquNQrzaXRLxilYFFfFoWixxMkrbcIZQBagcEBTXEmHEl5Ud2XFGasu2E9u/bVM/6V3K2icg6zLQt5WYO46R+g3ucRz04y3aWQy8bNxEN0JhDXg/gdwE8AOA5Zh45L48AOMtdnwXgYQBg5hERPY/GnPJUn7R2HlwFyoVM+czZn8l/BEHbM8PLIjqc82udo5x8Ys1fu5vOuXfb4FhHQEquHLmHFos4XJefadHVeXPb+ww7dngWB2jdWPmJ6oKUqUTcy3AhjJY5t8gx2SmKTzQH7x4knrV8TTO9VVaTYel1yUd684H7JqIdDD+G+zzb3xz1117EzcxjABcS0SkAPg/gjetNmIiuAnAVAODkXeuNbksi4gizUr2dFOF4lNisLW70KYQ+uAU/z/Lho/4mbzqIgxI2cM7irTdSwSIiz7CNcGfYnXpDoMk7slFLGTxBOzf/uTqhibdeRdhkPUHZxM266ktKHW7WDMW5z0azeTA4qq++cQeNW6Nv1fdsI6lsfQfB9bfBvqf+9cVUu0qY+Tki2gfgXQBOIaKh07rPBvCo8/YogFcDeISIhgBORrNIqeO6BsA1AEBnnaTyNM8sLjNI9WutTStNDq4BWDshZOOK3DLkm5yhoZ53antkeyPRIaJsdGxNs+5z4SSitUK1mJfhqmxcUgMOWwDdNUQZe8/J1kZZD1I2o36y90jLYZqFwg5ymcvg16POSH2BiSBMORPjn0GGKZGU5szR5eolE6Fzz/WqqCn3lKDPrpIzAaw50t4D4OfQLDjuA/ABNDtLPgzgCy7IDe7+6+75LTzD99HmOz4tK0Qjj6bTculBbKnj9pNgJAKG4q0FKeR2jERvDEr/Wq5cq+7SUmLi7PyKiBl1rLl3Jq0nBdRmK9KrpAhsHMniyyqUsSBv5Sd5mceSPQzAqdi2Ut1RMNpsEyLrUZgzaL69ZAqoU8OOHtCmim8d4bS39RB8r7BpPv16TRodxfb9qWLNo4/GvRfAdc7OXQH4LDPfSET3Avg0Ef1nAN8CcK3zfy2APyKiwwCeAfCrU8gToI/H3FFQnZONLWWtqZRVOKT20yjuyFMbmelHIRVDvYourqX2reVL/Lv/hNYZa+gqnLXFLpHF6Fw6Di1LKNSggrcavTQBie18iRicfvyAxTNT++ocZLWmm2QryUeIe4PNTNlvXc6CWcPlvoW5WSY2nV5W654QLnFe5yFTzHwAwEWG+4MALjbcXwbwK5Pi7UxzJ5O2BTmVF9WZbvcVbGLar0VARS42DG0vN98kfY2ORpzxR+hFTN1a6iSTSA8NV8qhbd4hHjbHxfjLRmqKIGY2jWKeIWwpT1IHk/uGfVZ2T/QONsc+OpVmbaq185OltyCTB61JJqqJJsQOLPGbk/bUY2dCNhSyneUjzlxDuOnouoxvWpROUa2OpS4swvb3fRrvRBky7r4sAhnr555c5WBmlHvyeryMw7fbZKrT/vjDw3Kaf5KOjsrwp59ZZbDRBGdF33f+v57Fyc2G2U5JPJ4seHsKIpLD37bUWSV2/S5rzS0ASSd3/2l+0afeIS7F8Aal1MoNfsgd5j+VvbRjR0PkNovGlQxGU0gWODdjy7dmI8Frh4lJyiVel/crEuFNTctc1Smnks0yn1gD+AzKKRtX3QJOiK1vF+470CRiseW4DvQotOwEKdagJ66HGHFvwW9OFpKeiBx5673BiR/DrJLROu2zO6aUMSx6Snc7PR1WvxEWTrBNIuwljOEmZJPkbS0C6t0iNeKwlRDO+YsWMINZRBBYJJKaVSZH66bH1XaagaLruMKJgiQqiCYOlcY8OTEL+y1UbdUyDxWcM2lP+8lWC30kMiezlFRiFktC3D2nyAUTps5aowuuaFlEaqyc+gs9d4I2GAJZdlpBSH2m+sJNTxs5yDoBHVPX1knkV1hF1E0bn7VlUvKh8YX4lBoz3ZhiusptvOpFS9kFLhWXOQgY9awVgpnRP3CyrmUp2x3FOTfMg4c6NHJgmjrNy7IkxF0wF1hbkqQ9VWp+ihHTKXKHthonqrxLjZsSb1m5O1LYePg89JhlWEQeaebquclA0U8rgt4h0XeNIUlHDNXy2dQTliVUphKRllDGTUAh7u2OaBGNYl62XrOXR5mmkRlu1uLaZO0pDQN74NlgJFydJSv/ObmMKWnSfRxVir4kbcmYJTOjfnvET6DsDGDTkB2gejnOFct41FIh7p0AbauV7oBY3xFaorVgCRi24I5GHbQ9i9zFdU4z3XA4u7SfwnLrZskTTElhH6BB5m1E3WWTEKMxYPYh88xYGTlOKlopJ3Nsk5/GbNYnrWl0giUkzBxmsmubJk2gT1kX4t4p6OwELRG1/o3XK7if9pHapQ2y9s6b2jm93VDuRGD486E17yZB5Q2hWUy0V5m6xWBOl+OIUzuvThZqWHH/MdUbSHwTtPZp0XcWsSCsS7vu0mHkbhFqT7mM+0rV21ZYiLuggTXdNnZarGsGndi8l6OzLgL9FqgyHoPFi8TgN2fThlycXbTZZIsj2rM9pzgLcRcgEEAEY3q8nl0GgrSnWl1fJDpVcAgzhWfSjAbeFTbv0ETX19Y7L41Vm7K63qxdEi15I7HeNkq6POeEQtwFUyyWrb/hTX3w1AJA3gQxcU+7G/DkDpI+2mlfLbZP+cxB246OO+2rXa+jLSzjYl8nZhSXlLIyT0WlEHdBBrYW3mf9zHSsmjiDHr/0fZcz16mfVuFWe727kL6qOp1ccu++N91PEteUw9iWGC6mWJTsm9wSk/ZGzgB13Gla05VLIe4CG6YWnlHNpzQPLL2JBADA8WYLAIlGLUaxoHDXSHZpZKKP0ZvQ3MJqzlwizVkzkSTF135GYWRjmUl4ZswxS1GRyZMhicC5r0b2TL8Qd8FUSLh7/krZFofeLWLbrvWEZqp90zrKiGs3bzFxawzAC0Ky136+naQQd8H6sB21ri5EC5apXcTbxz1MQiYYH9Hp+dJL2EUiHZCS97yxw6pZotcWWFF3yeL7BtRHIe6C/tjRnRfot2Cpw81b43aDhRFvb/KfFjttcJ4B9heb0p1U80Ih7oKC3kiPpwsvzQTCZKT7B9L98DB82cYH403VDhLYMPLeITBLtkdxth/IVusbyTk88yHwQtwFBVMg7peZxdpYlUa250ed2lhwzJlZigY8N0RlOY/xrvOLUiHRdSdTiLugYFZIE3cwnVifo5rxY3yFoDcX6yluxqbWVyHugoL1wDrSNYJB5nOdNFsiFcKfBetSuDd4F4lGIe6CgvWic6Ey14H70UQh4U3GrOXd9e3QDUAh7oKCmSHs1+JFRhvp5mtOnqvFzzm/Jl3QA+td2DXPSq+mOrK1DyYSNxHtBvBVALuc/88x828R0ScB/BSA553Xf8rM+6lRET4B4L0AXnLu35yLtAUFyw7rBSXzjRl7p0kaX9G4Nw0bshuH8nW7DvTRuI8BuIyZjxDRCoBbiejP3bN/w8yfU/5/AcB57u8SAL/nfgsKdh4ISEiaDbeCxWOOg+RGn4CZeWG+BTc44m5X3F+XPL8E4A9duNsAnEJEe9cvakHBVgSnfyQOhor+KP0r2HLYjHWJicQNAEQ0IKL9AJ4EcBMz3+4efYyIDhDR1US0y7mdBeBhEfwR56bjvIqI7iSiO/Hi8dlzUFCw7EgI2iDzooFvedAmDra9iJuZx8x8IYCzAVxMRG8F8FEAbwTwDgCnAfh30yTMzNcw89uZ+e04YXU6qQsKtgwatpb/gAog9devKxZsMMh9VmyWPxeDe3e2crv3N4bIp9pVwszPEdE+AFcw839xzseI6A8A/Gt3/yiAV4tgZzu3goJthVmnxGaoYhXZPggHtNOG1evEYZ6IziSiU9z1HgA/B+B+b7d2u0jeB+CgC3IDgH9CDd4J4HlmfnwDZC8oKCjYkeijce8FcB0RDdAQ/WeZ+UYiuoWIzkQzpuwH8M+d/y+i2Qp4GM12wF+bu9QFBQUFOxgTiZuZDwC4yHC/LOOfAXxk/aIVFBQUFFigZTgCkoh+COBFAE8tWpZNxBko+d3u2Gl53mn5BTY2z69h5jOtB0tB3ABARHcy89sXLcdmoeR3+2On5Xmn5RdYXJ7LHqSCgoKCLYZC3AUFBQVbDMtE3NcsWoBNRsnv9sdOy/NOyy+woDwvjY27oKCgoKAflknjLigoKCjogYUTNxFdQUSHiOgwEf3GouWZF4jo94noSSI6KNxOI6KbiOi77vdU505E9N9cGRwgop9YnOSzgYheTUT7iOheIrqHiH7duW/LPBPRbiK6g4i+7fL7n5z7uUR0u8vXZ4ho1bnvcveH3fNzFpqBGeEOnPsWEd3o7rd7fh8ioruJaD8R3encFt6mF0rc7m3M30VzhvebAXyQiN68SJnmiE8CuEK5/QaAm5n5PAA3u3sgPsP8KjRnmG81jAD8K2Z+M4B3AviIq8vtmmd/Tv0FAC4EcIU74uG3AVzNzK8H8CyAK53/KwE869yvdv62In4dwH3ifrvnFwB+hpkvFNv+Ft+mmXlhfwDeBeBL4v6jAD66SJnmnL9zABwU94cA7HXXewEcctf/A8AHLX9b9Q/AF9Cca7Pt8wzgFQC+ieaDIU8BGDr30L4BfAnAu9z10PmjRcs+ZT7PRkNUlwG4Ec1xF9s2v072hwCcodwW3qYXbSrpdXb3NsKruD1w6wcAXuWut1U5uGnxRQBuxzbOM6lz6gE8AOA5Zh45LzJPIb/u+fMATt9UgdeP/wrg36L9OObp2N75BZpz/r5MRHcR0VXObeFtunwseEFgZiaibbelh4hOBPBnAP4FM/9IHn263fLMzGMAF7rTMz+P5nz6bQki+rsAnmTmu4jopxcszmbi3cz8KBG9EsBNRHS/fLioNr1ojXunnd39hDgOdy8aTQ3YJuVAzTdJ/wzAHzPz9c55W+cZaM6pB7APjangFCLyCpHMU8ive34ygKc3V9J14VIAf5+IHgLwaTTmkk9g++YXAMDMj7rfJ9EMzhdjCdr0oon7GwDOcyvTqwB+Fc153tsVNwD4sLv+MBo7sHff0meYU6NaXwvgPmb+uHi0LfNM9jn196Eh8A84bzq/vhw+AOAWdobQrQBm/igzn83M56Dpp7cw8z/GNs0vABDRCUR0kr8GcDma7w4svk0vgfH/vQC+g8Y++B8WLc8c8/UnAB4HsIbG1nUlGhvfzQC+C+AvAZzm/BKa3TUPALgbwNsXLf8M+X03GnvgATTns+93dbst8wzgfADfcvk9COA3nftrAdyB5jz6PwWwy7nvdveH3fPXLjoP68j7TwO4cbvn1+Xt2+7vHs9Py9Cmy5uTBQUFBVsMizaVFBQUFBRMiULcBQUFBVsMhbgLCgoKthgKcRcUFBRsMRTiLigoKNhiKMRdUFBQsMVQiLugoKBgi6EQd0FBQcEWw/8HIXPmKaDl8nIAAAAASUVORK5CYII=\n",
57 | "text/plain": [
58 | ""
59 | ]
60 | },
61 | "metadata": {
62 | "needs_background": "light"
63 | },
64 | "output_type": "display_data"
65 | }
66 | ],
67 | "source": [
68 | "circles=circles[0,:]\n",
69 | "for i in circles:\n",
70 | " cv2.circle(rgb_img,(int(i[0]),int(i[1])),int(i[2]),(0,255,255),2)\n",
71 | " cv2.circle(rgb_img,(int(i[0]),int(i[1])),2,(0,255,255),3)\n",
72 | "# contours, hierarchy = cv2.findContours(detected_edges, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)\n",
73 | "circles0 = cv2.HoughCircles(dice0,cv2.HOUGH_GRADIENT,1.2,20,param1=50,param2=25,minRadius=3,maxRadius=35)\n",
74 | "circles1 = cv2.HoughCircles(dice1,cv2.HOUGH_GRADIENT,1.2,20,param1=50,param2=25,minRadius=3,maxRadius=35)\n",
75 | "print(len(circles0[0]), len(circles1[0]))\n",
76 | "plt.imshow(rgb_img)\n",
77 | "plt.show()"
78 | ]
79 | },
80 | {
81 | "cell_type": "code",
82 | "execution_count": null,
83 | "id": "51d1fe2b-a068-4ba2-af33-fc6ea17ff79f",
84 | "metadata": {},
85 | "outputs": [],
86 | "source": []
87 | }
88 | ],
89 | "metadata": {
90 | "kernelspec": {
91 | "display_name": "Python 3 (ipykernel)",
92 | "language": "python",
93 | "name": "python3"
94 | },
95 | "language_info": {
96 | "codemirror_mode": {
97 | "name": "ipython",
98 | "version": 3
99 | },
100 | "file_extension": ".py",
101 | "mimetype": "text/x-python",
102 | "name": "python",
103 | "nbconvert_exporter": "python",
104 | "pygments_lexer": "ipython3",
105 | "version": "3.7.9"
106 | }
107 | },
108 | "nbformat": 4,
109 | "nbformat_minor": 5
110 | }
111 |
--------------------------------------------------------------------------------